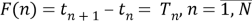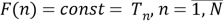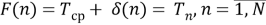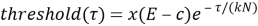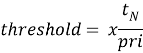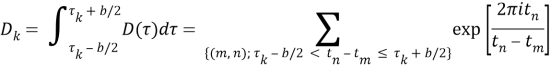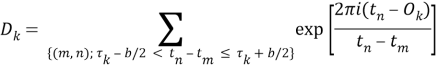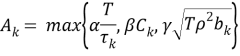В статье рассмотрены типы модуляции сигнала по периоду и наиболее популярные и эффективные алгоритмы селекции, использующие исключительно время прихода импульсов. Проведено исследование, позволяющее для каждого типа сигнала подобрать оптимальный алгоритм.
Ключевые слова: алгоритмы селекции, ЦОС, период повторения импульсов, MATLAB, радиотехнический контроль, гистограмма накопительных разностей, гистограмма последовательных разностей.
Радиотехника является ключевой технологией во многих сферах жизнедеятельности человека в современном мире. Она применяется в таких областях как телекоммуникации, электроника, авиация, космонавтика, промышленность и т. д.
Задача разделения смеси сигналов
Важными направлениями в радиотехнике являются проектирование и применение средств радиотехнического контроля (РТК). Задача деинтерливинга (разделения) смеси радиолокационных сигналов, одна из главных составляющих системы РТК, представляет собой процесс обнаружения импульсных последовательностей, принадлежащих различным, одновременно активным источникам радиоизлучения (ИРИ).
Методы для решения этой задачи основаны на анализе различных параметров радиолокационных импульсов, например, таких параметров как время прихода, амплитуда, длительность импульса и т. д. Наиболее информативным параметром является период повторения импульсов (ППИ) [1], поэтому в этой статье будут рассмотрены алгоритмы, которые используют только информацию о времени прихода импульса (ВПИ). К таким алгоритмам относятся гистограмма последовательных разностей (SDIF), гистограмма накопительных разностей (CDIF), а также алгоритм Discrete PRI Transform и его усовершенствованный вариант — Modified PRI Transform. Эти методы позволяют найти предполагаемые периоды во входной импульсной последовательности, после чего может быть выполнена попытка извлечь последовательность импульсов с заданным периодом. Таким образом из входной смеси будут поочередно извлечены сигналы, принадлежащие различным ИРИ.
Для разработки усовершенствованного алгоритма селекции смесей сигналов, который будет эффективен в сложной радиоэлектронной обстановке (РЭО), необходимо проанализировать особенности каждого типа сигналов и подобрать для них наиболее подходящие методы деинтерливинга.
Цель и задачи
Таким образом, целью настоящей статьи является выбор наиболее эффективных алгоритмов деинтерливинга на основе типа модуляции сигнала. Для достижения поставленной цели должны быть решены следующие задачи:
— Провести анализ особенностей сигналов с различными типами модуляции по периоду
— Провести анализ различных алгоритмов деинтерливинга и их особенностей
— Написать код на MATLAB для расчета точности нахождения корректных периодов в зависимости от процента пропущенных импульсов в общем импульсном потоке
— Для разных алгоритмов, сигналов и их смесей построить графики, демонстрирующие эту зависимость
— Проанализировать полученные результаты и сделать соответствующие выводы
Типы сигналов
В современных РЛС используются различные виды межимпульсной модуляции. Рассмотрим основные сигналы, классифицированные в зависимости от типа модуляции по периоду.
Обозначим время прихода
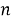
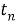
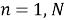
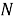
|
|
(1) |
Stable или constant . Это сигнал с постоянным периодом повторения импульсов.
|
|
(2) |
Stagger.
Это сигнал с изменением периода от импульса к импульсу, то есть существует фиксированная последовательность, состоящая из 2 и более периодов, которая повторяется [3]. Предположим, что такая последовательность
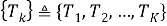
|
|
(3) |
Jitter. Это сигнал со случайным изменением ППИ.
|
|
(4) |
δ(n) — это случайное дрожание и оно не должно превышать 30 % от среднего значения
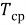
Описание алгоритмов
Гистограмма последовательных разностей (S DIF ). Данный алгоритм основан на анализе значений экстремумов гистограммы последовательных разностей ВПИ. Для начала строится гистограмма первой разности. После обработки этой гистограммы и последовательного поиска сигналов, если входная последовательность содержит достаточное количество импульсов, строится новая гистограмма второй разности и т. д. Блок-схема алгоритма приведена на рисунке 1.
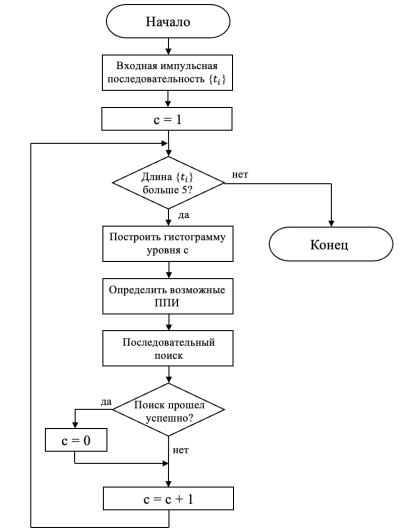
Рис. 1. Блок-схема алгоритма SDIF
В данном методе также используется порог обнаружения, который значительно повышает эффективность алгоритма [4]:
|
|
(5) |
где
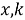
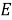
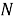
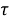
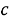
Гистограмма накопительных разностей (C DIF ). Этот алгоритм также основан на анализе значений пиков гистограммы разностей ВПИ. Но если для SDIF каждый раз строится новая гистограмма, которая не учитывает вычисления, полученные на предыдущем шаге, то CDIF накапливает результаты в одной гистограмме. Блок-схема алгоритма приведена на рисунке 2.
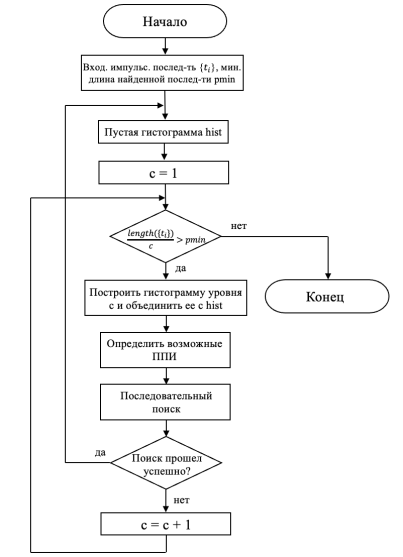
Рис. 2. Блок-схема алгоритма CDIF
В этом методе также используется порог обнаружения, который сокращает количество вычислений [5]:
|
|
(6) |
где
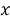
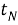
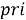
Discrete PRI Transform . В этом методе также анализируются пики гистограммы, но значительно отличается способ её построения. В описанных ранее алгоритмах значение каждого бина гистограммы — количество разностей, которое попало в этот бин, в данном методе значение каждой ячейки вычисляется по следующей формуле [6]:
|
|
(7) |
где
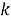
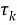
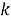
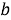
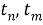
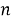
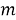
Modified PRI Transform . Этот метод является усовершенствованной версией алгоритма Discrete PRI Transform, в нем используются следующие улучшения [7]:
— Перекрывающиеся ячейки гистограммы
— Смещение начала отсчёта времени
Формула (7) в данном алгоритме принимает следующий вид:
|
|
(8) |
где
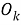
— Порог обнаружения, основанный на трех критериях: критерии по времени наблюдения, критерии для устранения субгармоник и критерии для устранения шума:
|
|
(9) |
где
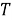
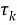
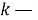
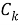
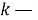
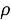
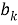
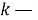
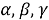
Описание алгоритма для расчета точности нахождения корректных периодов в зависимости от процента пропущенных импульсов
На качество радиотехнического мониторинга значительное влияние оказывают помехи, которые приводят к снижению эффективности, надежности и точности контроля, а также ограничивают возможности связи и мониторинга. Наличие помех является причиной того, что из сигнала может быть потеряно какое-то количество импульсов, поэтому важно оценить эффективность алгоритмов в зависимости от процента пропущенных импульсов в сигнале.
Что бы проанализировать эту зависимость, на языке программирования MATLAB была написана функция, которая удаляет заданный процент случайно выбранных импульсов из входной импульсной последовательности, затем выполняет поиск предполагаемых периодов и сравнивает полученный результат с ожидаемым, вычисляя при этом отношение корректно найденных периодов к числу всех периодов.
Так как из входной смеси удаляются импульсы, выбранные случайным образом, то результаты работы алгоритма деинтерливинга будут зависеть от того, какие именно импульсы были удалены.
В качестве примера рассматривается stable-сигнал с периодом 100, состоящий из 10 импульсов. Массив TOA — время прихода этих импульсов. PRI — это разность между соседними элементами TOA. Из всех возможных вариантов на рисунке 3 приведены два конкретных варианта как именно могут быть удалены 36 % импульсов. В первом случае удаление приведет к тому, что появится новый период 200 и в массиве ППИ он будет встречаться чаще чем реальный — 100, поэтому именно период 200 и будет обнаружен. То есть точность нахождения периода в этому случае будет 0 %. В то время как во втором случае удаление импульсов никак не повлияет на нахождение корректного периода и точность составит 100 %.
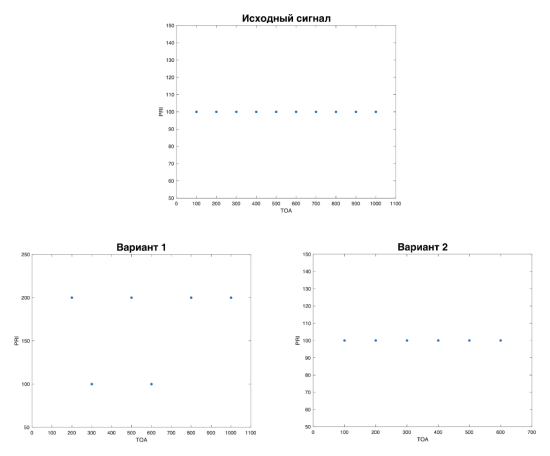
Рис. 3. Пример удаления импульсов из stable-сигнала
Таким образом, случайность рассматриваемого процесса оказывает существенное влияние на результаты поиска предполагаемых периодов. Что бы минимизировать влияние случайности процесса можно использовать метод Монте-Карло [8]. Тогда происходит многократные удаление импульсов и расчет точности обнаружения периодов, после чего вычисляется среднее арифметическое полученных значений, которое и используется в дальнейшем.
Далее описанный процесс повторяется уже для нового процента удаленных импульсов.
Анализ полученных результатов
Что бы для каждого типа сигналов подобрать оптимальный алгоритм деинтерливинга были рассмотрены смеси из:
— 2 stable-сигналов
— 2 stagger-сигналов
— 1 stable и 1 stagger-сигнала
— 1 stable и 1 jitter-сигнала
— 1 stable, 1 stagger и 1 jitter-сигнала.
Для каждой такой смеси построены графики зависимости точности нахождения корректных периодов от процента пропущенных импульсов в общем импульсном потоке. Графики представлены на рисунка 4–8.
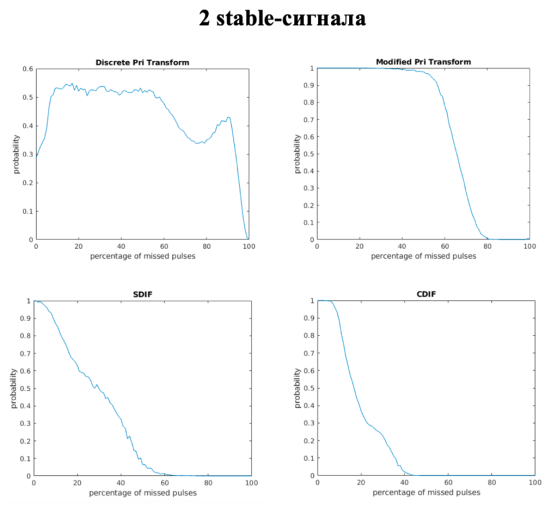
Рис. 4. Графики зависимости точности нахождения периодов от процента пропущенных импульсов для смеси из 2 stable-сигналов
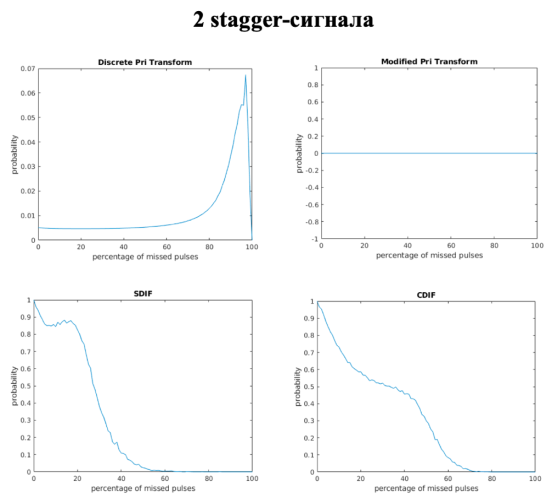
Рис. 5. Графики зависимости точности нахождения периодов от процента пропущенных импульсов для смеси из 2 stagger-сигналов
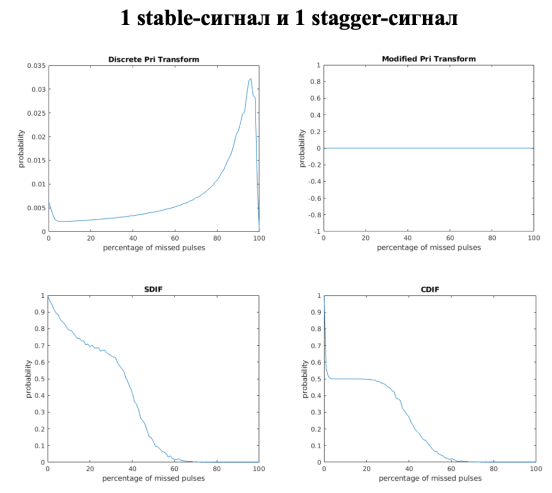
Рис. 6. Графики зависимости точности нахождения периодов от процента пропущенных импульсов для смеси из 1 stable и 1 stagger-сигнала
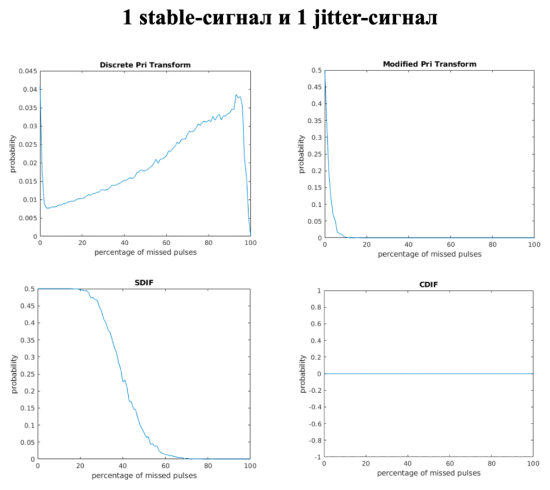
Рис. 7. Графики зависимости точности нахождения периодов от процента пропущенных импульсов для смеси из 1 stable и 1 jitter-сигнала
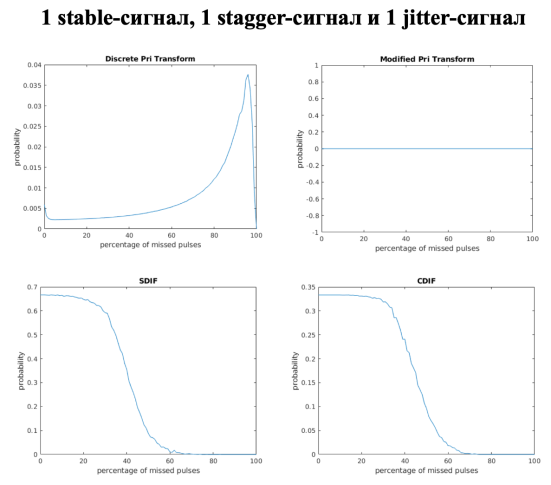
Рис. 8. Графики зависимости точности нахождения периодов от процента пропущенных импульсов для смеси из 1 stable, 1 stagger и 1 jitter-сигнала
По полученным графикам можно сделать выводы об оптимальности каждого алгоритма для разных смесей, которые приведены в таблице 1.
Таблица 1
Сравнение эффективности алгоритмов для смесей сигналов
|
SDIF |
CDIF |
Discrete PRI Transform |
Modified PRI Transform |
|
|
Смесь из 2 stable-сигналов |
|
|
|
|
|
Смесь из 2 stagger-сигналов |
|
|
|
|
|
Смесь из 1 stable и 1 stagger-сигнала |
|
|
|
|
|
Смесь из 1 stable и 1 jitter-сигнала |
|
|
|
|
|
Смесь из 1 stable, 1 stagger и 1 jitter-сигнала |
|
|
|
|
Таким образом, для извлечения из смесей сигналов типа stable и jitter эффективно использовать алгоритм SDIF, он достаточно точен и наиболее устойчив к удалению импульсов. А для извлечения stagger-сигнала наиболее подходящим является алгоритм CDIF, он не самый эффективный на смеси трёх сигналов, но при анализе смеси из 2 stagger-сигналов он показал наилучший результат.
В ходе выполнения данной работы для сигналов с различными типами модуляции по периоду были подобраны наиболее эффективные алгоритмы деинтерливинга. Результаты данного исследования позволят разработать усовершенствованный комбинированный метод разделения смесей сигналов, который будет обладать высокой точностью селекции в сложной радиоэлектронной обстановке.
Литература:
1. Терентьев А. В., Коротков В. Ф. Радиотехническая разведка: Теория и практика обработки радиолокационных сигналов. ‒ СПб.: Медиапапир, 2021. ‒ 27 c.
2. Tang, Y., He, M., Tang, X., Han, J. and Fan, X. (2019), Method for automatically identifying PRI patterns of complex radar signals. The Journal of Engineering, 2019: 6975–6978. https://doi.org/10.1049/joe.2019.0487
3. Korotkov V. F., Zyryanov R. S. Pulse Sequence Division in Mixed Signal Flow. Izvestiya Vysshikh Uchebnykh Zavedenii Rossii. Radioelektronika [Journal of the Russian Universities. Radioelectronics]. 2017, no. 3, pp. 5–10. (In Russian)
4. Jia, J.; Han, Z.; Liu, L.; Xie, H.; Lv, M. Research on the SDIF Failure Principle for RF Stealth Radar Signal Design. Electronics 2022, 11, 1777. https://doi.org/10.3390/ electronics11111777
5. Mardia, H. K. New techniques for the deinterleaving of repetitive sequences. IEE Proceedings F-Radar and Signal Pro- cessing. 1989, vol. 136, no. 4, pp. 149–154.
6. Y. Mao, J. Han, G. Guo and X. Qing, «An Improved Algorithm of PRI Transform», 2009 WRI Global Congress on Intelligent Systems, Xiamen, China, 2009, pp. 145–149, doi: 10.1109/GCIS.2009.313.
7. Nishiguchi, Ken'ichi and Masaaki Kobayashi. “Improved algorithm for estimating pulse repetition intervals.” IEEE Trans. Aerosp. Electron. Syst. 36 (2000): 407–421.
8. G. Fishman, «Generating samples» in Monte Carlo: Concepts Algorithms and Applications, New York, NY, USA:Springer, 1996.