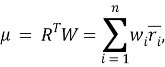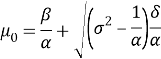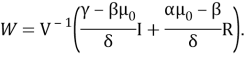Построение оптимального инвестиционного портфеля с прогнозом доходностей активов методами машинного обучения



В статье рассматривается составление портфеля из акций 79 российских компаний. Для прогнозирования ожидаемой доходности акций используется архитектура рекуррентной нейронной сети LSTM. Оптимальный портфель ценных бумаг определяется при помощи современной портфельной теории Г. Марковица.

Ключевые слова: машинное обучение, портфель Марковица, нейронные сети.

Введение

Инвестиции являются одним из факторов экономического роста и благосостояния государства и его жителей. Однако для многих частных инвесторов самостоятельно сформировать инвестиционный портфель является сложной задачей, ведь процесс управления портфелем связан с постоянным анализом финансовых активов, оценкой их будущей доходности и рисков в условиях постоянного роста объемов доступных рыночных данных. Возможным решением данного вопроса может служить использование интеллектуальных систем, способных упростить процесс управления портфелем. Так, в статье рассматривается задача построения оптимального портфеля, в котором алгоритм машинного обучения используется для нахождения вектора ожидаемых доходностей акций.

Основная часть

Задача построения оптимального портфеля основана на портфельной теории, созданной Г. Марковицем в 1952 году [1]. В данной работе рассмотрена задача построения оптимального портфеля в следующей постановке [2]: найти удельные веса активов в портфеле, обеспечивающем заданный риск с максимальной доходностью

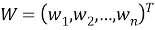
Тогда для построения оптимального портфеля необходимо в пространстве весов

найти максимум целевой функции

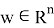
(1)

при условиях

	(2)
	(3)

где R — вектор доходностей активов, V — ковариационная матрица активов, и I — единичный вектор.

В нашей задаче разрешены короткие продажи, поэтому веса будут принимать как отрицательные, так и положительные значения.

Введем следующие обозначения:

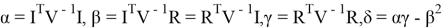
Тогда задача нахождения оптимального портфеля с целевой функцией (1) при условиях (2–3) имеет следующий алгоритм решения:

1. Найти значения констант
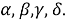
2. Для заданного значения риска рассматриваем уравнение относительно доходности μ ;
3. Находим наибольший корень этого уравнения по формуле:

(4)

4. Находим веса портфеля по формуле:

(5)

Доходности активов могут быть найдены на основе их среднеарифметического значения. Это хорошо работает на больших сроках инвестирования, однако, чем он меньше, тем более непредсказуемой может быть доходность. Альтернативой исторической доходности может быть прогнозирование доходности с помощью методов машинного обучения.

В данной работе прогнозирующей моделью взята рекуррентная нейронная сеть LSTM, способная изучать долговременные зависимости [3], что очень полезно для прогнозирования временных рядов.

Обучающим набором будут данные о дневных доходностях акций 79 российских компаний, собранных за годичный период с 01.04.2022 по 31.04.2023, период восстановления торгов после их приостановки из-за обвала в феврале 2022 года. Модель будет прогнозировать доходности акций на следующий день торгов после обозначенного периода. Соответственно итоговые веса в портфеле будут обозначать, какие активы мы должны купить или продать в последний день года, чтобы получить максимальную доходность на следующий день.

Важный этап обработки полученных данных, использованный в данном исследовании — создание окон данных. Метод скользящего окна является основным методом обработки временного ряда при рекуррентной архитектуре нейронной сети. Метод скользящего окна — это алгоритм, помогающий генерировать набор обучающих данных из членов временного ряда для построения прогнозной модели. Так, в этой работе было создано 4 набора данных с размером окна 5, 10, 15 и 20 дней со смещением в один временной шаг, чтобы модель предсказывала значение доходности на один день вперед.

Модель нейронной сети в данной работе состоит из двух слоев. Первый слой — LSTM с 50 нейронами, в которой используется сигмоидальная функция активации по умолчанию. Выходной плотный слой имеет 79 нейронов по количеству активов, входящих в портфель.

Для конфигурации данной модели в качестве метода оптимизации был использован алгоритм Adam, функцией потерь взята средняя квадратичная ошибка (Mean Squared Error — MSE), а отслеживаемой метрикой стала средняя абсолютная ошибка (Mean Absolute Error — MAE).

Таким образом было создано четыре модели с одинаковой архитектурой, которые обучались на окнах данных разного временного шага. На рис. 1 отражены предсказания сети LSTM для обучающих, валидационных и тестовых данных одной из акций.

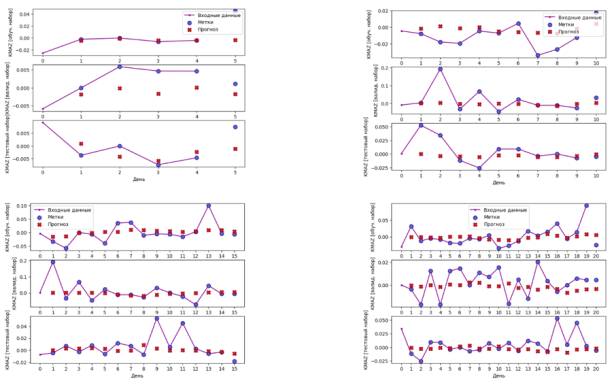
Рис. 1. Визуализация предсказаний сети LSTM на окнах ширины 5, 10, 15, 20 дней

Для сравнения показателей ошибки MAE для разного количества дней в обучающих данных были построены столбчатые диаграммы приведенные на рис. 2. Видно, что показатели ошибки почти одинаковые, но предсказание доходности на тестовых данных модели, обучавшейся на окнах размером 10 дней, наилучшая. В связи с этим принимаем размер окна в 10 дней оптимальным для задачи предсказания доходностей акций на один день в будущее.

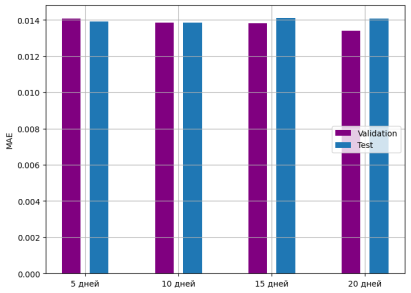
Рис. 2. Показатели ошибки модели

Используя предсказания модели, обучавшейся на 10-дневных окнах данных, получили вектор ожидаемых доходностей акций. Его отсортированный и идентифицированный вид представлен в таблице 1. Так, ожидается, что доходности акций МТС (MTSS) и Лензолото (LNZL) будут наибольшими на предсказываемый день, а именно 0.015848 (1.58 %) и 0.015621 (1.56 %).

Таблица 1

Ожидаемые доходности акций российских компаний

FIVE	-0.00804	MSTT	-0.00101	GAZA	0.001865	MRKP	0.005392
TRNFP	-0.00663	AQUA	-0.00085	POLY	0.002243	CBOM	0.005566
CHMF	-0.00576	DSKY	-0.00065	AFLT	0.002647	SBER	0.00619
NKNC	-0.00545	RTKM	-0.0006	APTK	0.002649	TATN	0.006266
MRKZ	-0.00521	MTLR	-0.00059	MRKC	0.002753	MOEX	0.006471
ENPG	-0.00494	BSPB	-0.00029	USBN	0.003017	UPRO	0.00689
PHOR	-0.00453	LPSB	-3.17E-05	UTAR	0.003036	MRKS	0.006938
MVID	-0.00446	VTBR	-5.49E-06	ABRD	0.003106	GMKN	0.007332
SELG	-0.0044	HYDR	5.61E-05	AGRO	0.003276	PIKK	0.007526
NLMK	-0.00438	GLTR	0.00015	MGNT	0.003314	PLZL	0.00764
VSMO	-0.00433	SFIN	0.000265	RASP	0.003405	TGKA	0.008425
ALRS	-0.00316	FESH	0.000303	RNFT	0.003551	OZON	0.009456
OKEY	-0.00312	LSRG	0.00067	MAGN	0.004134	VKCO	0.009851
RUAL	-0.00295	SVAV	0.000903	MRKV	0.004139	FLOT	0.010151
AMEZ	-0.00249	YNDX	0.000954	QIWI	0.004142	ETLN	0.011777
TRMK	-0.00217	MSRS	0.001194	CIAN	0.00415	BRZL	0.011838
AKRN	-0.00183	MRKU	0.001237	ROSN	0.004276	GAZP	0.012193
ZILL	-0.00166	AFKS	0.001296	TCSG	0.004439	LNZL	0.015621
MSNG	-0.00157	IRAO	0.001596	LKOH	0.004488	MTSS	0.015848
NVTK	-0.00125	KMAZ	0.001652	NMTP	0.004627

После того, как были получены ожидаемые доходности активов в портфеле, оптимальный портфель максимальной доходности может быть найден по формулам (4–5). В данном численном эксперименте приведен портфель максимальной доходности с заданным риском 0.03. При таких параметрах и спрогнозированными доходностями были получены веса портфеля приведенные в таблице 2.

Таблица 2

Веса активов в оптимальном портфеле

SELG	-0.79684	FESH	-0.13955	SVAV	0.000661	UTAR	0.208551
CHMF	-0.62299	NKNC	-0.13424	POLY	0.001669	OZON	0.214993
LSRG	-0.61191	GLTR	-0.11551	PHOR	0.005253	BRZL	0.23299
ENPG	-0.49401	LKOH	-0.11135	MTLR	0.012511	AGRO	0.249306
MVID	-0.47125	BSPB	-0.10996	GAZP	0.030637	MRKS	0.260343
ALRS	-0.45422	TCSG	-0.06642	YNDX	0.034935	UPRO	0.273667
RTKM	-0.44408	MRKV	-0.06439	OKEY	0.065034	TGKA	0.288457
TRNFP	-0.43587	DSKY	-0.054	NMTP	0.0698	CBOM	0.350239
FIVE	-0.42729	AMEZ	-0.05256	ROSN	0.070802	PLZL	0.351235
MRKZ	-0.32853	KMAZ	-0.0509	RASP	0.072557	FLOT	0.373037
MSNG	-0.31464	ABRD	-0.05006	LNZL	0.094566	PIKK	0.447842
TRMK	-0.2829	NVTK	-0.04755	USBN	0.098788	MOEX	0.448283
NLMK	-0.24841	VSMO	-0.04621	VKCO	0.100729	AFLT	0.463624
AQUA	-0.21313	SBER	-0.04589	ZILL	0.11903	MSRS	0.490031
VTBR	-0.20699	GAZA	-0.0309	QIWI	0.119345	MAGN	0.532655
AKRN	-0.20018	IRAO	-0.02495	MRKC	0.136758	GMKN	0.618206
HYDR	-0.19541	LPSB	-0.01752	ETLN	0.14814	APTK	0.626091
RUAL	-0.19439	MRKU	-0.01737	RNFT	0.153989	TATN	0.627166
CIAN	-0.19024	MRKP	-0.00827	MGNT	0.18837	MTSS	0.697121
AFKS	-0.14872	MSTT	-0.00213	SFIN	0.1943

Доходность такого портфеля на прогнозируемый день составляет 0.08237027675608861 (8 %), что должно являться максимальной возможной доходностью при риске, заданном как 0.03.

Проверить это можно с помощью визуализации эффективной границы, например, сгенерировав несколько тысяч портфелей со случайным распределением акций.

Визуализируя сгенерированные портфели и портфель, полученный в ходе применения теории Марковица, на графике отношения риска к доходности видно, что полученный нами портфель, лежит на эффективной границе, это значит, что он соответствует заданному параметру максимальной доходности для риска равного 0.03 (рис. 3).

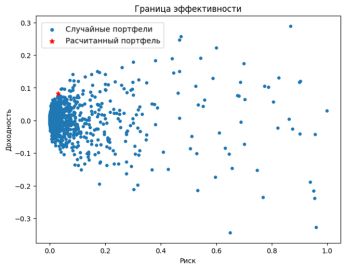
Рис. 3 График портфелей с различным распределением активов

Заключение

В ходе данной работы был описан принцип построения оптимального портфеля и способ усовершенствования его точности с помощью модели прогнозирования будущих доходностей акции, основанной на методе машинного обучения. Рассмотрено обучение рекуррентной нейронной сети LSTM, способной вычислять вектор ожидаемых доходностей на следующий торговый день. Используя полученные данные и алгоритм построения оптимального портфеля, были получены доли, с которыми должны быть взяты активы в портфель, для получения максимального дохода.

Литература:

1. Markowitz, H. (1952). Portfolio Selection. Journal of Finance, 7, 77–91. doi:10.2307/2975974.
2. Шорохов, Сергей Геннадьевич. Управление портфелями финансовых активов [Текст]: учебное пособие / С. Г. Шорохов. — Москва: Российский ун-т дружбы народов, 2013. — 95 с.: ил., табл.; 21 см.; ISBN 978–5–209–05417–7
3. Sherstinsky, A. (2018). Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) Network. ArXiv, abs/1808.03314.