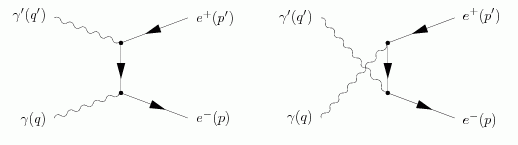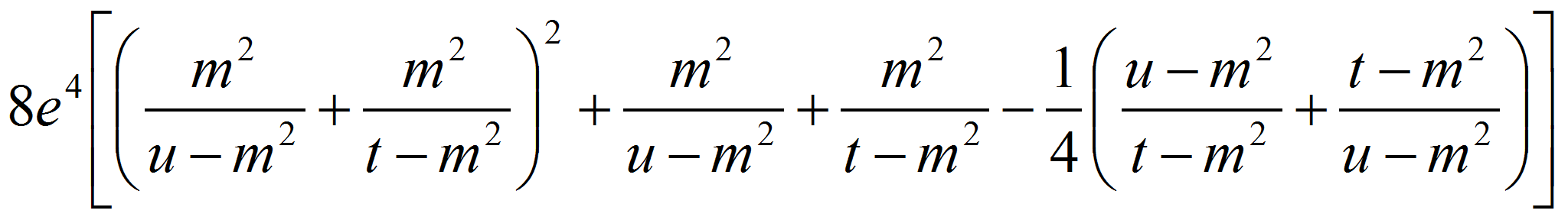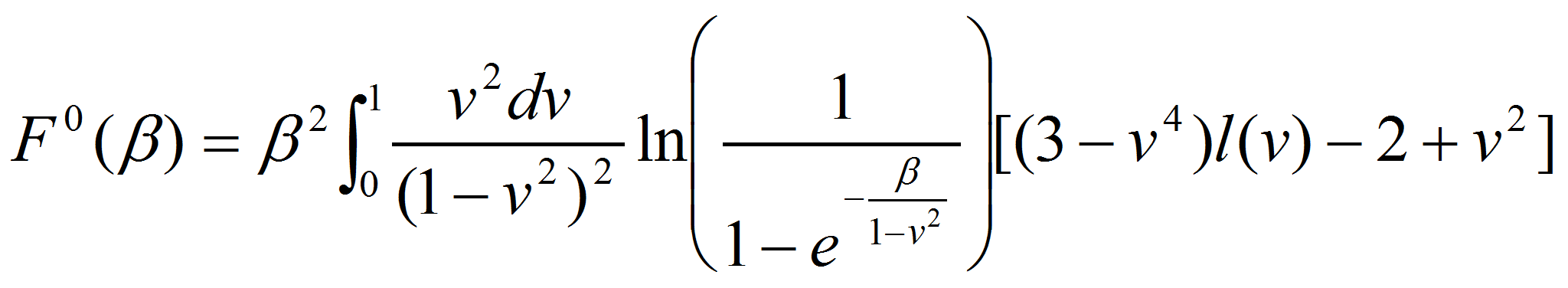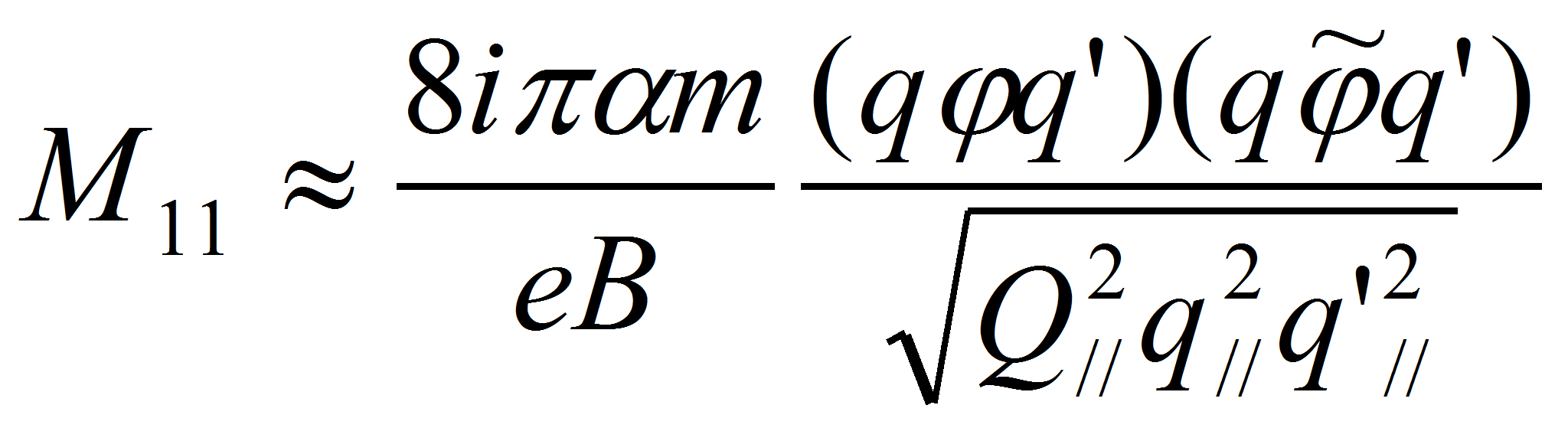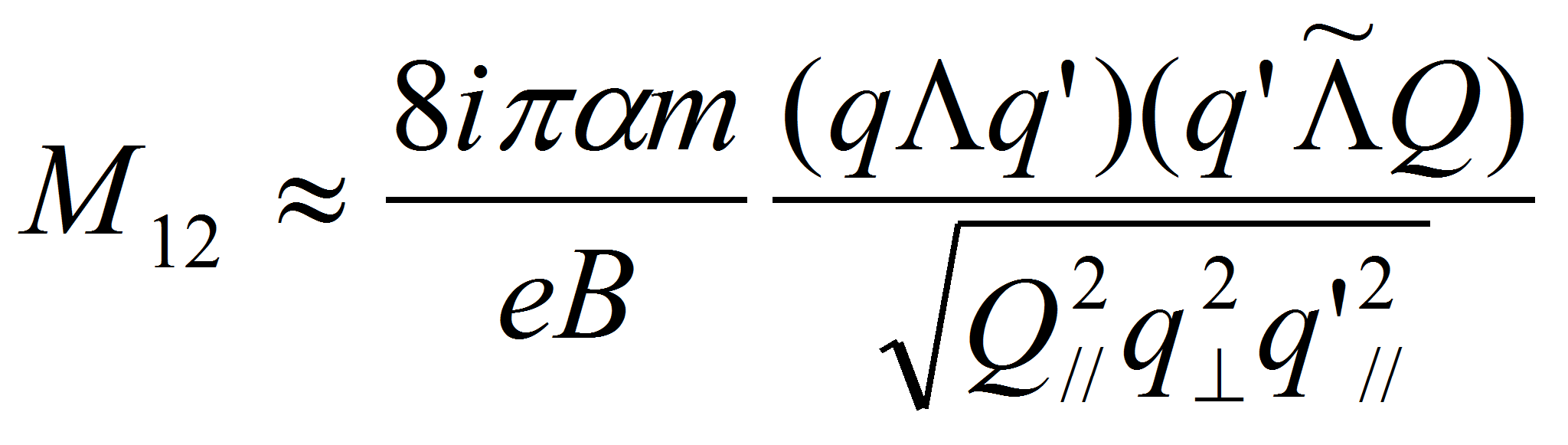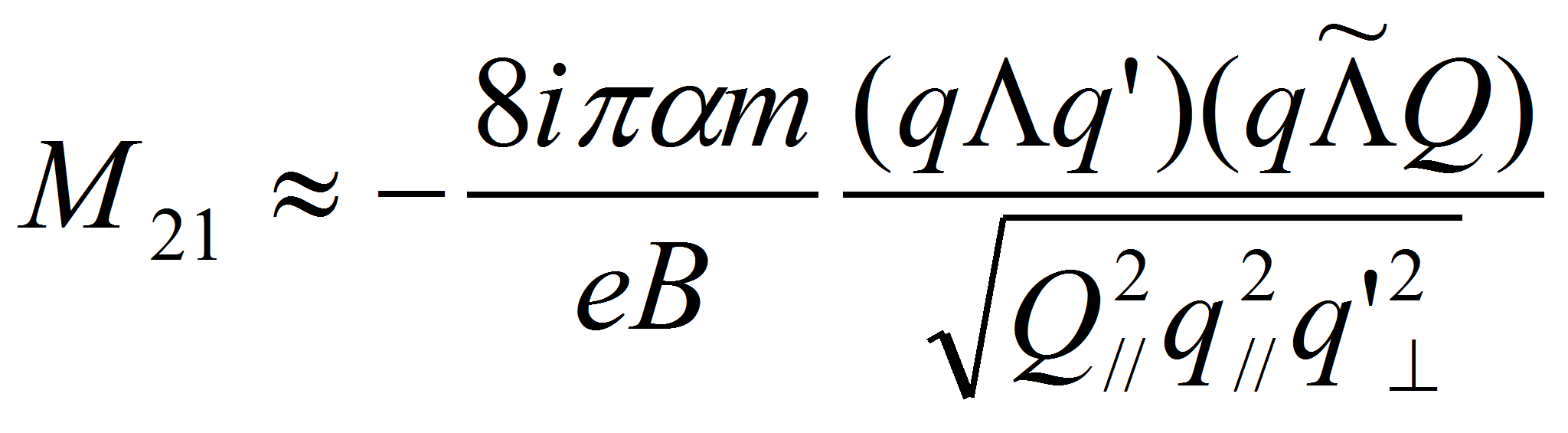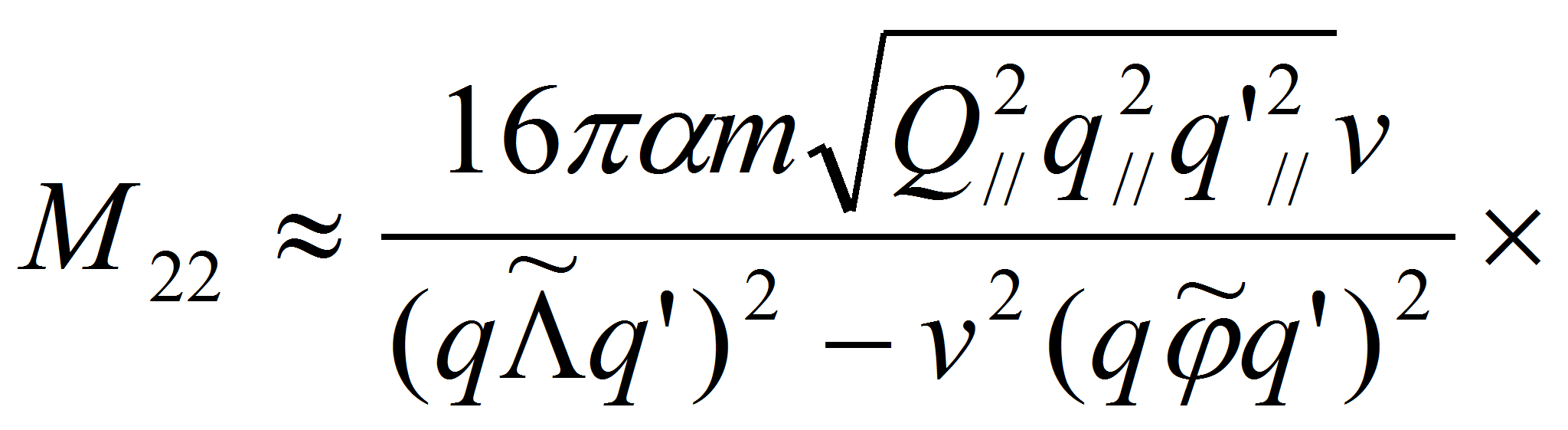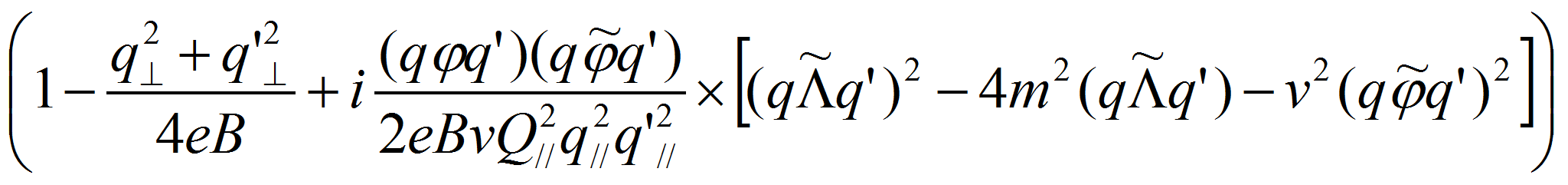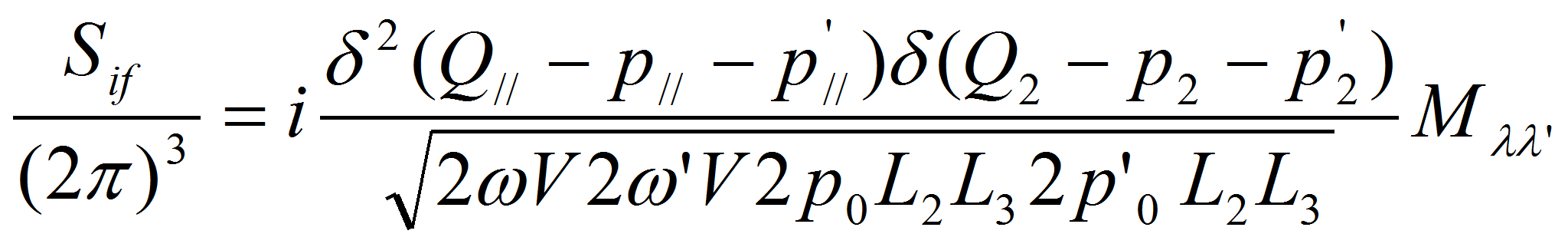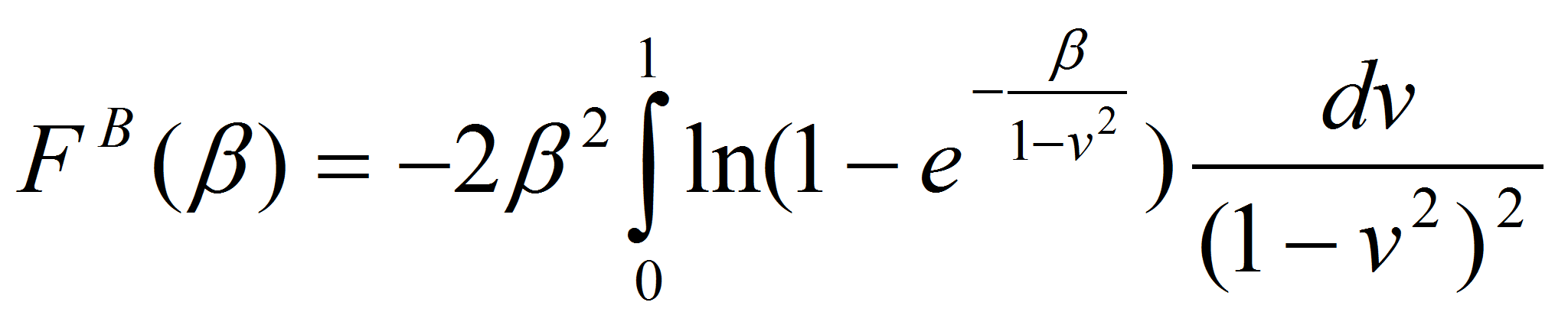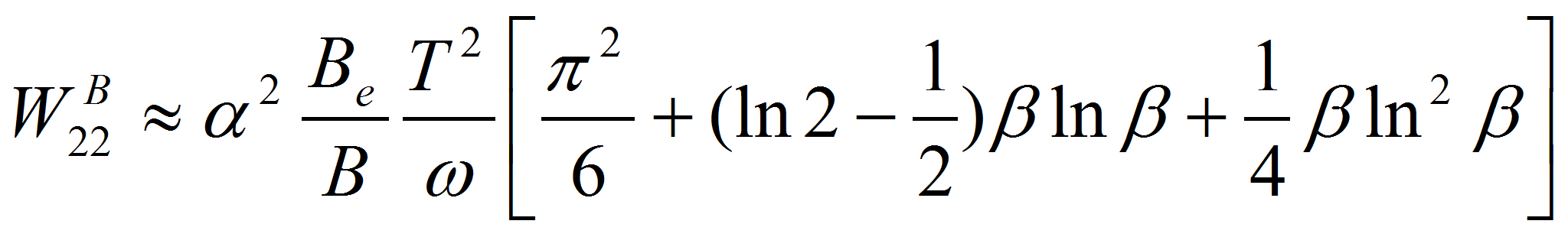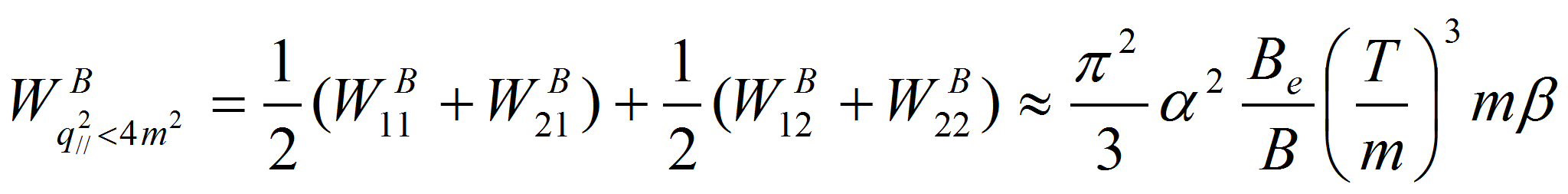Введение
Даная работа посвящена изучению процесса рождения
![]() пар при распространении фотона в термальной бане. Задача
рассматривается как в условиях отсутствия магнитного поля так и в
сильном магнитном поле, напряжённость которого много больше так
называемого критического значения
пар при распространении фотона в термальной бане. Задача
рассматривается как в условиях отсутствия магнитного поля так и в
сильном магнитном поле, напряжённость которого много больше так
называемого критического значения
![]()
![]() 1,
где m - масса электрона.
1,
где m - масса электрона.
Существует целый ряд астрофизических объектов, в которых реализуются
экстремальные физические условия (![]()
![]() ).
До недавного времени считалось, что наиболее сильные магнитные поля
существуют в пульсарах - астрофизических объектах, которые
ассоциируются с быстро вращающимися нейтронными звёздами. У
большинства пульсаров наблюдается уменьшение периода вращения со
временем, что обычно связывается с потерями кинетической энергии
вращения за счёт магнитодипольного излучения. Тогда для стандартных
параметров нейтронных звёзд,
).
До недавного времени считалось, что наиболее сильные магнитные поля
существуют в пульсарах - астрофизических объектах, которые
ассоциируются с быстро вращающимися нейтронными звёздами. У
большинства пульсаров наблюдается уменьшение периода вращения со
временем, что обычно связывается с потерями кинетической энергии
вращения за счёт магнитодипольного излучения. Тогда для стандартных
параметров нейтронных звёзд,
![]() ,
,
![]() см,
напряжённости магнитного поля у большинства пульсаров не превосходят
см,
напряжённости магнитного поля у большинства пульсаров не превосходят
![]() Гс.
Однако в начале 90-х годов была предложена теоретическая модель
генерации магнитного поля внутри нейтронной звезды с величиной
напряжённости вплоть до
Гс.
Однако в начале 90-х годов была предложена теоретическая модель
генерации магнитного поля внутри нейтронной звезды с величиной
напряжённости вплоть до
![]() Гс
[1,2]. Нейтронные звёзды с магнитным полем
Гс
[1,2]. Нейтронные звёзды с магнитным полем
![]()
![]() получили название «магнитаров». Такое сильное магнитное
поле может генерироваться вследствии очень быстрого вращения
нейтронной звезды (
получили название «магнитаров». Такое сильное магнитное
поле может генерироваться вследствии очень быстрого вращения
нейтронной звезды (![]() мс)
на самых ранних этапах её образования.
мс)
на самых ранних этапах её образования.
Существует ещё один класс астрофизических явлений, в
которых, в принципе, может генерироваться сверхсильное магнитное
поле. К нему относится процесс взрыва сверхновой типа II. Сверхновые
этого типа связывают с молодыми массивными звёздами. Поэтому вспышки
сверхновых считаюся конечной стадией эволюции звёзд с массой
![]() .
На этой стадии вначале происходит коллапс, а затем сброс оболочки с
образованием остатка в виде нейтронной звезды или черной дыры.
.
На этой стадии вначале происходит коллапс, а затем сброс оболочки с
образованием остатка в виде нейтронной звезды или черной дыры.
В условиях сильного магнитного поля некоторые процессы, кинематически
запрещенные в вакууме, становятся допустимыми. Среди них следует
указать распад фотона на
![]() пару, который может быть ответственен за рождение
пару, который может быть ответственен за рождение
![]() плазмы. В ряде работ [3,4] показано, что в условиях сильного (
плазмы. В ряде работ [3,4] показано, что в условиях сильного (![]() )
магнитного поля данный процесс может быть подавлен по сравнению с
процессом распада фотона на пару более мягких фотонов:
)
магнитного поля данный процесс может быть подавлен по сравнению с
процессом распада фотона на пару более мягких фотонов:
![]() ,
который также запрещен в вакууме. Это имеет место, даже, несмотря на
то, что однофотонное рождение пары является процессом первого порядка
по теории возмущений, а распад фотона на пару фотонов третьего.
Следует отметить, однако, что если фотон движется под острым углом к
магнитному полю
,
который также запрещен в вакууме. Это имеет место, даже, несмотря на
то, что однофотонное рождение пары является процессом первого порядка
по теории возмущений, а распад фотона на пару фотонов третьего.
Следует отметить, однако, что если фотон движется под острым углом к
магнитному полю
![]() так, что
так, что
![]() (ось z направлена вдоль поля), то процесс
(ось z направлена вдоль поля), то процесс
![]()
![]() оказывается кинематически запрещен. Обычно полагается, что при
движении фотона в магнитном поле с искривленными силовыми линиями
угол между векторами
оказывается кинематически запрещен. Обычно полагается, что при
движении фотона в магнитном поле с искривленными силовыми линиями
угол между векторами
![]() и
и
![]() увеличивается и
увеличивается и
![]() уменьшается
так, что
уменьшается
так, что
![]() могло бы превысить пороговое значение
могло бы превысить пороговое значение
![]() .
Однако, как было отмечено в работах [5-8], учет дисперсии фотона в
сильном магнитном поле приводит к специфическому явлению захвата
фотона магнитным полем. Таким образом, если фотон родился в
кинематической области
.
Однако, как было отмечено в работах [5-8], учет дисперсии фотона в
сильном магнитном поле приводит к специфическому явлению захвата
фотона магнитным полем. Таким образом, если фотон родился в
кинематической области
![]() ,
он в ней и останется, несмотря на искривление силовых линий
магнитного поля.
,
он в ней и останется, несмотря на искривление силовых линий
магнитного поля.
В связи с этим становится интересным процесс
столкновения фотона, летящего под острым углом к магнитному полю (![]() ),
с мягким термальным фотоном в сильном магнитном поле. В данной работе
рассматривается процесс рождения
),
с мягким термальным фотоном в сильном магнитном поле. В данной работе
рассматривается процесс рождения
![]() пары фотоном большой энергии при его распространении в термальной
бане как в условиях без поля так и в сильном магнитном поле. В ходе
исследования произведён расчёт вероятности рождения
пары фотоном большой энергии при его распространении в термальной
бане как в условиях без поля так и в сильном магнитном поле. В ходе
исследования произведён расчёт вероятности рождения
![]() пары в единицу времени. Вычислена длина свободного пробега фотона
высокой энергии, распространяющегося сквозь термодинамически
равновесный фотонный газ вдоль силовых линий магнитного поля так, что
процесс распада
пары в единицу времени. Вычислена длина свободного пробега фотона
высокой энергии, распространяющегося сквозь термодинамически
равновесный фотонный газ вдоль силовых линий магнитного поля так, что
процесс распада
![]()
![]() запрещён кинематически. Показано, что сильное магнитное поле
оказывает подавляющее влияние на данный процесс.
запрещён кинематически. Показано, что сильное магнитное поле
оказывает подавляющее влияние на данный процесс.
2. Рождение
![]() пар фотоном в термальной бане в отсутствии магнитного поля
пар фотоном в термальной бане в отсутствии магнитного поля
В настоящей главе мы рассмотрим процесс рождения
![]() пар при прохождении фотона высокой энергии (
пар при прохождении фотона высокой энергии (![]() )
сквозь термодинамически равновесный фотонный газ с температурой
)
сквозь термодинамически равновесный фотонный газ с температурой
![]() в отсутствии магнитного поля. Данный процесс
в отсутствии магнитного поля. Данный процесс
![]() изображается двумя диаграммами Фейнмана (см. рис.1).
изображается двумя диаграммами Фейнмана (см. рис.1).
Рис. 1: Диаграммы Фейнмана, описывающие процесс
![]()
Амплитуды, соответствующие диаграммам, имеют вид:
где
![]() -
вектора поляризации фотонов,
-
вектора поляризации фотонов,
![]() ,
,
![]() -
матрицы Дирака,
-
матрицы Дирака,
![]() биспинор, описывающий электрон, а черта в обозначении
биспинор, описывающий электрон, а черта в обозначении
![]() -
дираковски сопряжённый биспинор.
-
дираковски сопряжённый биспинор.
Квадрат амплитуды процесса удобно сформулировать в терминах инвариантных переменнных Мандельстама:
здесь ведётся суммирование по поляризациям электронов
![]() и
усреднение по поляризациям фотонов
и
усреднение по поляризациям фотонов
![]() .
.
Нетрудно найти сечение данного процесса:
здесь
![]() ,
,
![]() -
постоянная тонкой структуры, а переменная
-
постоянная тонкой структуры, а переменная
![]() имеет физический смысл скорости электрона (позитрона) в системе
центра инерции.
имеет физический смысл скорости электрона (позитрона) в системе
центра инерции.
Зная выражение для сечения
![]() можно получить вероятность процесса фоторождения
можно получить вероятность процесса фоторождения
![]() в
единицу времени:
в
единицу времени:
где индекс «0» означает, что расчет производится без
учета магнитного поля,
![]() и
и
![]() -
энергии начальных жесткого и термального фотонов соответственно, а
-
энергии начальных жесткого и термального фотонов соответственно, а
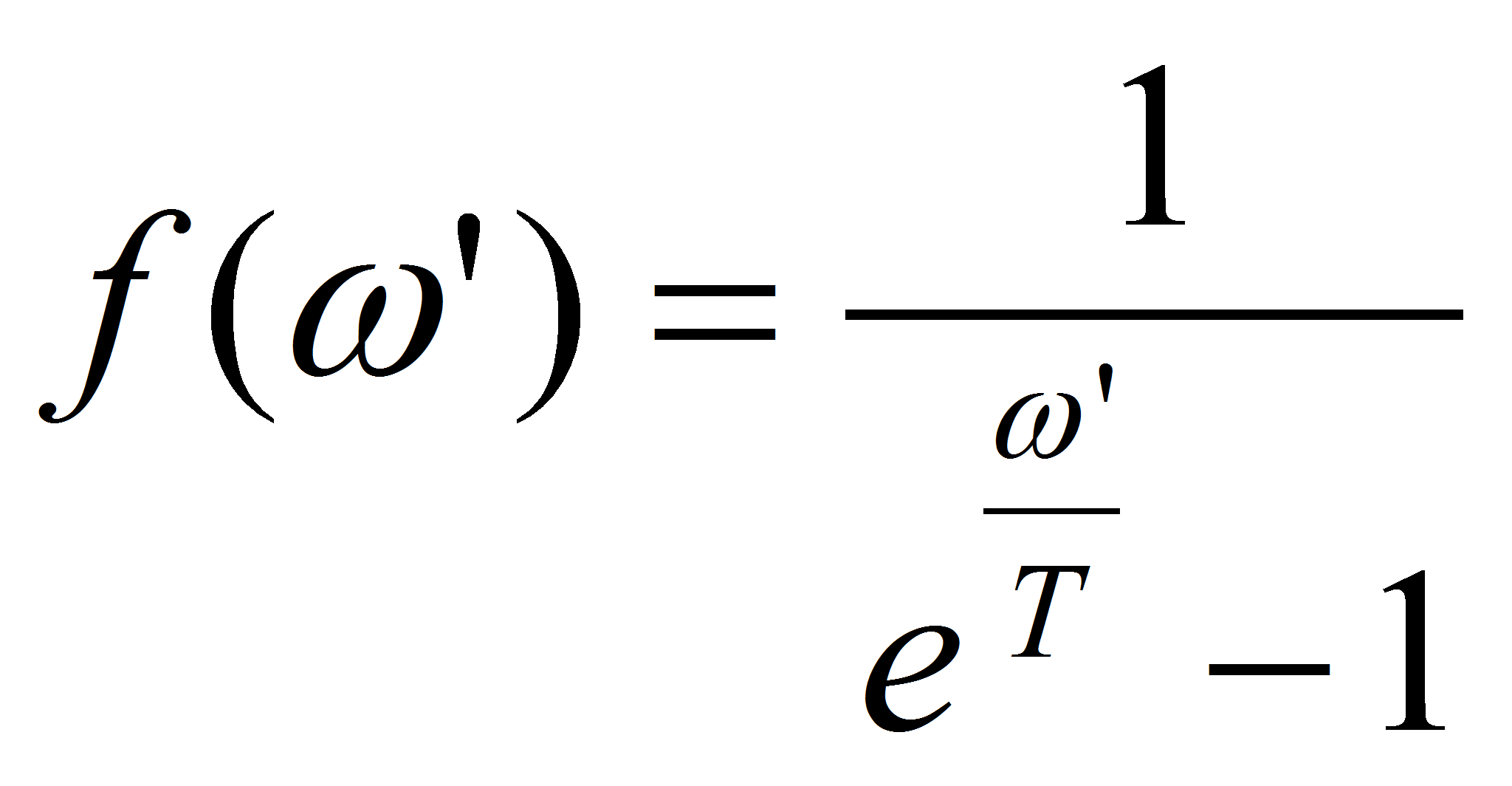 равновесная функция распределения фотонов с температурой
равновесная функция распределения фотонов с температурой
![]() по
энергиям.
по
энергиям.
Для изотропного термального распределения задача значительно упрощается и вероятность процесса без учёта магнитного поля в единицу времени можно представить в виде однократного интеграла:
где
здесь введены переменная
![]() ,
и функция
,
и функция
![]() .
.
3. Рождение
![]() пар жестким фотоном в замагниченной термальной бане
пар жестким фотоном в замагниченной термальной бане
В этой главе нами рассматривается процесс
![]() при распространении жесткого фотона в замагниченной термальной
бане под острым углом к силовым линиям магнитного поля так, что
выполняется условие
при распространении жесткого фотона в замагниченной термальной
бане под острым углом к силовым линиям магнитного поля так, что
выполняется условие
![]() .
Данный процесс изображается теми же диаграммами (рис.1), однако, в
данном случае волновые функции электронов описываются решениями
уравнения Дирака в магнитном поле. В пределе сильного магнитного поля
электроны и позитроны занимают основной уровень Ландау и выражения,
описывающие их волновые функции, значительно упрощаются. Мы
используем калибровку
.
Данный процесс изображается теми же диаграммами (рис.1), однако, в
данном случае волновые функции электронов описываются решениями
уравнения Дирака в магнитном поле. В пределе сильного магнитного поля
электроны и позитроны занимают основной уровень Ландау и выражения,
описывающие их волновые функции, значительно упрощаются. Мы
используем калибровку
![]() ,
где магнитное поле направлено вдоль оси
,
где магнитное поле направлено вдоль оси
![]() .
.
Используя результаты работы [9], в которой исследовался процесс комптоновского рассеяния фотона на электроне, амплитуды рассматриваемого процесса могут быть представлены в виде:
где
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() -
тензор электромагнитного поля, а
-
тензор электромагнитного поля, а
![]() дуальный ему тензор.
дуальный ему тензор.
![]() ,
,
![]() связаны
соотношением
связаны
соотношением
![]() .
В данном выражении использовалось разложение 4-вектора на продольную
и поперечную компоненты:
.
В данном выражении использовалось разложение 4-вектора на продольную
и поперечную компоненты:
![]() ,
,
![]() ,
,
![]() .
Индекс у амплитуды соответствует поляризациям фотонов, участвующих во
взаимодействии. Первый индекс соответствует поляризации жесткого
фотона, второй - поляризации термального фотона.
.
Индекс у амплитуды соответствует поляризациям фотонов, участвующих во
взаимодействии. Первый индекс соответствует поляризации жесткого
фотона, второй - поляризации термального фотона.
Напомним, что мы рассматриваем случай, когда жесткий фотон движется
под острым углом к силовым линиям магнитного поля (![]() )
так, что
)
так, что
![]() и
процесс
и
процесс
![]()
![]() кинематически запрещен. В данной кинематической области имеет
место «захват» фотона силовыми линиями магнитного поля
[5-8].
кинематически запрещен. В данной кинематической области имеет
место «захват» фотона силовыми линиями магнитного поля
[5-8].
Для того чтобы найти вероятность рождения
![]() пар в единицу времени жестким фотоном в термальной бане,
необходимо просуммировать по всем возможным квантовым состояниям
выражение:
пар в единицу времени жестким фотоном в термальной бане,
необходимо просуммировать по всем возможным квантовым состояниям
выражение:
где
![]() - полное время взаимодействия,
- полное время взаимодействия,
![]() ,
,
![]() ,
,
![]() .
S-матричный элемент и амплитуда процесса
.
S-матричный элемент и амплитуда процесса
![]() в сильном магнитном поле связаны соотношением:
в сильном магнитном поле связаны соотношением:
Интегрирование по
![]() и
и
![]() не вызывает затруднений, а интегрирование по импульсам термальных
фотонов
не вызывает затруднений, а интегрирование по импульсам термальных
фотонов
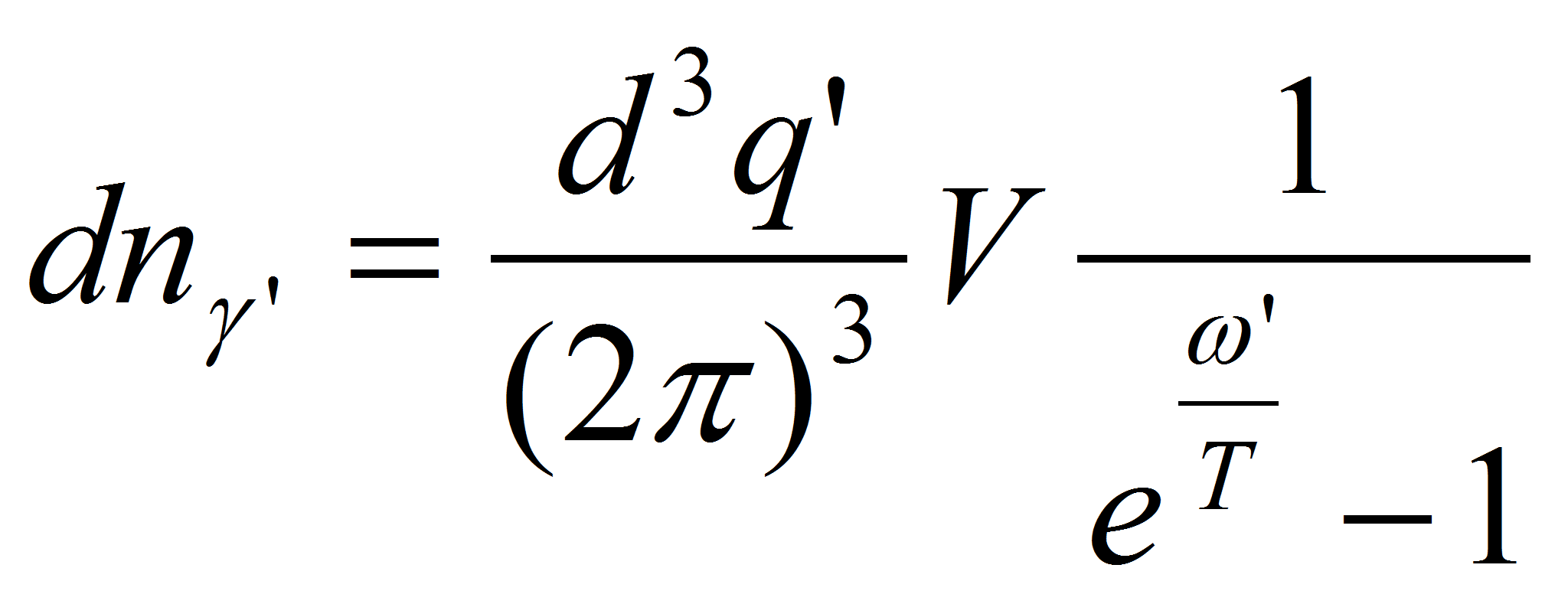 в том случае, когда они имеют поляризацию
в том случае, когда они имеют поляризацию
![]() усложняется. Это связано с тем, что закон дисперсии таких фотонов в
сильном магнитном поле отличается от вакуумного, что изменяет фазовый
объем. Вычисления вероятностей процессов с участием фотонов с
поляризацией
усложняется. Это связано с тем, что закон дисперсии таких фотонов в
сильном магнитном поле отличается от вакуумного, что изменяет фазовый
объем. Вычисления вероятностей процессов с участием фотонов с
поляризацией
![]() дают
следующий результат:
дают
следующий результат:
В cлучае, когда оба фотона имеют поляризацию
![]() ,
вероятность процесса в единицу времени можно представить в виде
однократного интеграла:
,
вероятность процесса в единицу времени можно представить в виде
однократного интеграла:
где
![]() .
Если жёсткий фотон имеет достаточно большую энергию, чтобы
выполнялось условие
.
Если жёсткий фотон имеет достаточно большую энергию, чтобы
выполнялось условие
![]() ,
справедливо разложение:
,
справедливо разложение:
Таким образом, для вероятности в единицу времени процесса рождения
![]() пары
неполяризованным жестким фотоном на термальном фотонном газе
получаем:
пары
неполяризованным жестким фотоном на термальном фотонном газе
получаем:
Если сравнить выражения для вероятностей процесса в
отсутствии поля (6) и в сильном магнитном поле (18) нетрудно видеть,
что сильное магнитное поле увеличивает длину пробега, т.е. подавляет
рассматриваемый процесс фоторождения
![]() пар.
Для оценки фактора подавления можно использовать отношение длин
свободного пробега:
пар.
Для оценки фактора подавления можно использовать отношение длин
свободного пробега:
где функции
![]() и
и
![]() определены
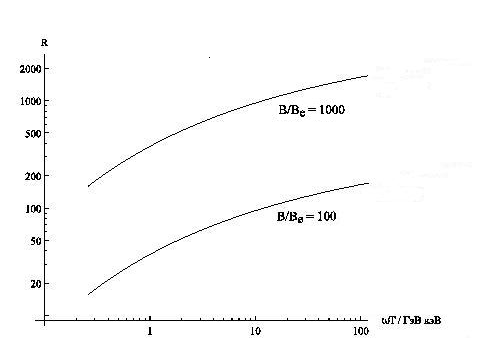
формулами (7) и (16). Зависимость фактора подавления
определены
формулами (7) и (16). Зависимость фактора подавления
![]() от
энергии фотона для
от
энергии фотона для
![]() и
и
![]() приведена на рис.2.
приведена на рис.2.
Рис. 2: Зависимость фактора подавления процесса
![]() от
энергии фотона
от
энергии фотона
в сильном магнитном поле.
4. Заключение
В данной работе рассматривалась задача о рождении
![]() пар при распространении фотона высокой энергии, движущегося под
острым углом к силовым линиям сильного магнитного поля через фотонный
газ. Был изучен процесс рождения
пар при распространении фотона высокой энергии, движущегося под
острым углом к силовым линиям сильного магнитного поля через фотонный
газ. Был изучен процесс рождения
![]() пар фотоном большой энергии (
пар фотоном большой энергии (![]() )
при его распространении в термальной бане как в условиях без поля так
и в сильном магнитном поле. Вычислены вероятности рождения
)
при его распространении в термальной бане как в условиях без поля так
и в сильном магнитном поле. Вычислены вероятности рождения
![]() пары в единицу времени (6) и (18). Сравнение выражений для
вероятностей процесса в отсутствии поля (6) и в сильном магнитном
поле (18) показало, что сильное магнитное поле подавляет рождение
пары в единицу времени (6) и (18). Сравнение выражений для
вероятностей процесса в отсутствии поля (6) и в сильном магнитном
поле (18) показало, что сильное магнитное поле подавляет рождение
![]() пар. Построен график зависимости фактора подавления
пар. Построен график зависимости фактора подавления
![]() от
энергии начального фотона
от
энергии начального фотона
![]() .
.
Литература:
Duncan R.C., Thompson C. Formation of very strongly magnetized neutron stars: implications for gamma-ray bursts // Astrophys. J. 1992.V. 392, № 1.P. L9-L13.
Thompson C., Duncan R.C. Neutron star dynamos and the origins of pulsar magnetism //Astrophys. J. 1993.V. 408, № 1.P.194-217.
M.G. Baring, A.K. Harding, Radio Quiet Pulsars with Ultrastrong Magnetic Fields, Astrophys. J. (1998) Vol. 507. L55-L58.
M.G. Baring, A. K. Harding, Photon Splitting and Pair Creation in Highly Magnetized Pulsars, Astrophys. J. (2001) Vol. 547. P. 929-948.
A.E. Шабад, Поляризация вакуума и квантового релятивистского газа во внешнем поле, Тр. ФИАН СССР «Поляризационные эффекты во внешних калибровочных полях», Наука, Москва (1988) Т. 192.
A.E. Shabad, Cyclotronic Resonance in the Vacuum Polarization, Lett. Nuovo Cimento (1972) Vol. 3, N 11, P. 457-460.
A.E. Shabad, V.V. Usov,
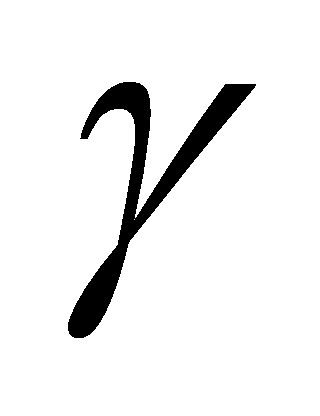 -Quanta
capture by magnetic field and pair creation suppression in pulsars,
Nature (1982) Vol. 295, P. 215-217.
-Quanta
capture by magnetic field and pair creation suppression in pulsars,
Nature (1982) Vol. 295, P. 215-217.В.В. Усов, А.Е. Шабад, Светопозитроний в магнитосфере пульсара, Письма в ЖЭТФ (1985) Т. 42, C. 17-20.
D.A. Rumyantsev, M.V. Chistyakov, Compton Effect in Strongly Magnetized Plasma, International Journal of Modern Physics A (2009) Vol. 24. P. 3995-4008.
Kuznetsov A.V., Mikheev N.V.: Electroweak Processes in External Electromagnetic Fields. New York: Springer-Verlag, 2003.
1
Все вычисления проводятся в естественной системе единиц
![]() ,
,
![]() -
элементарный заряд.
-
элементарный заряд.