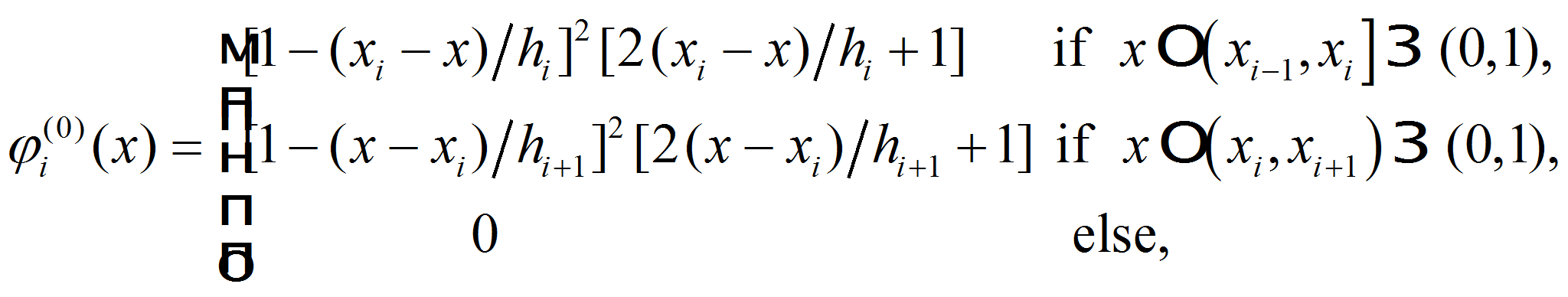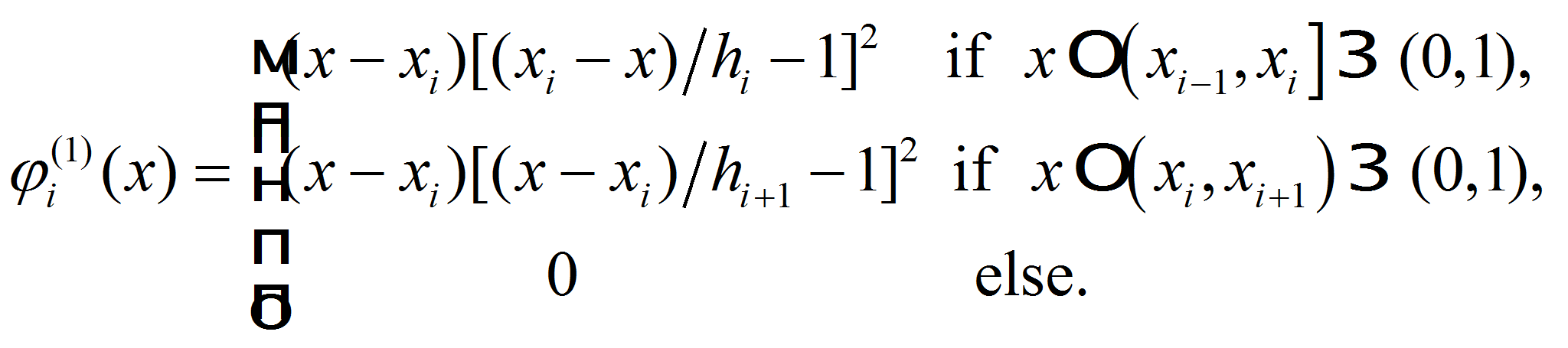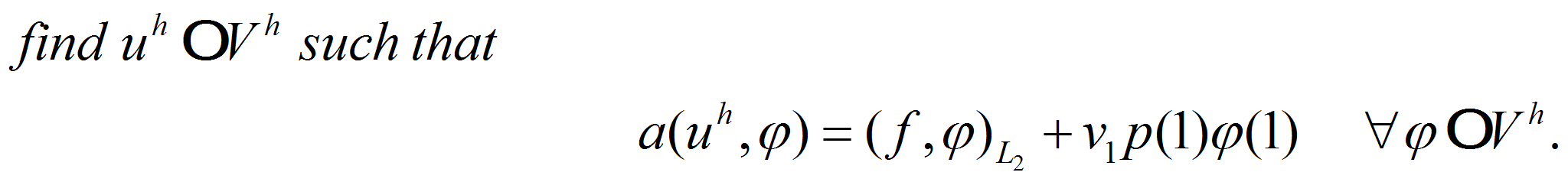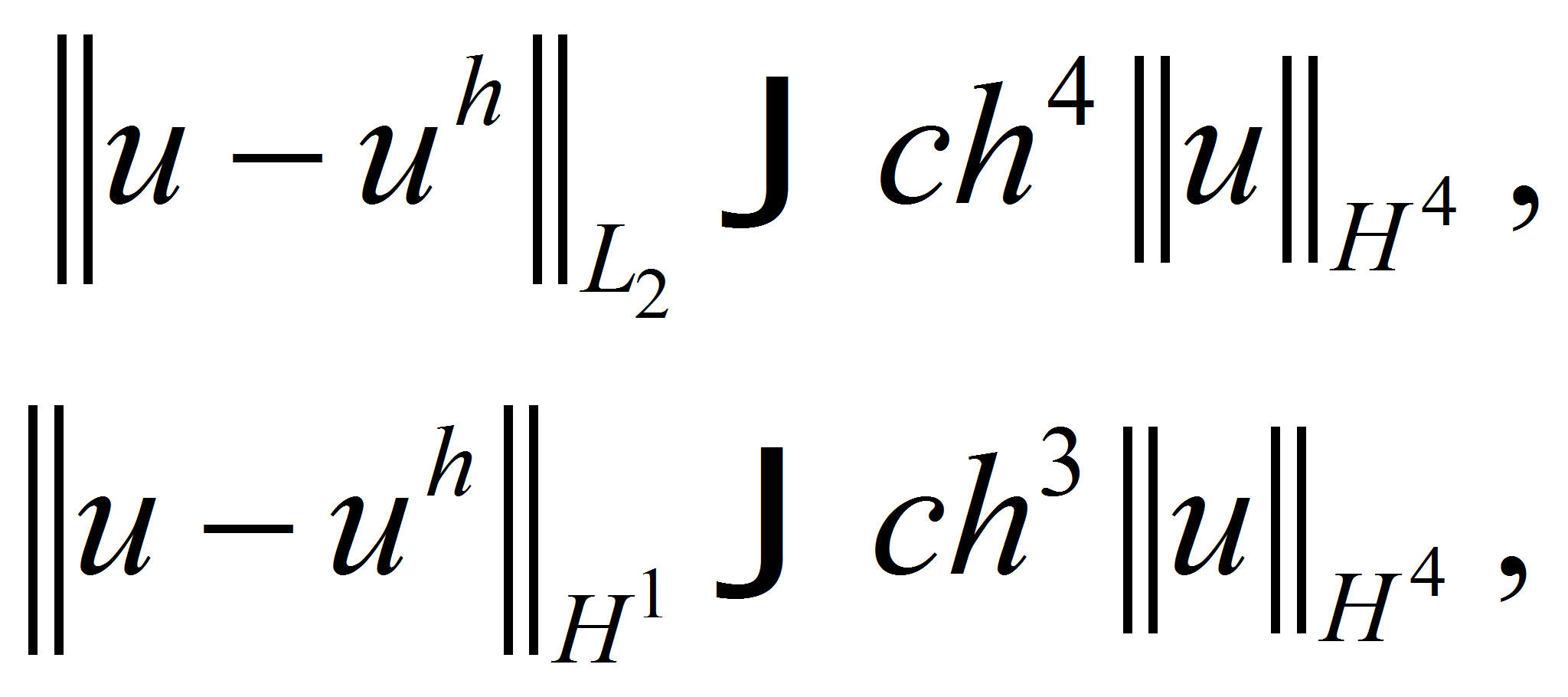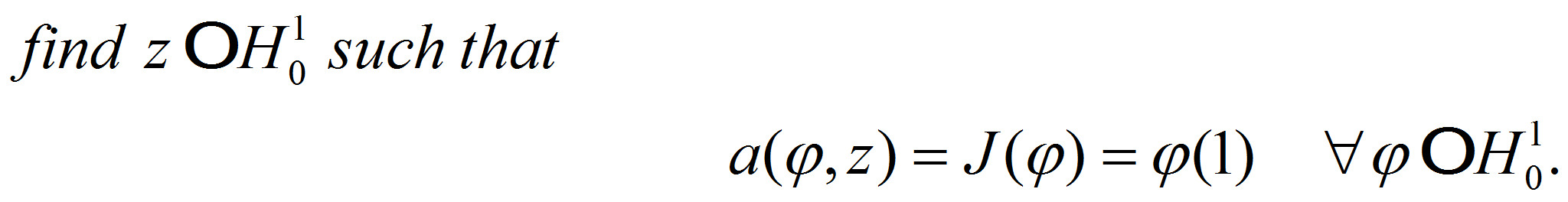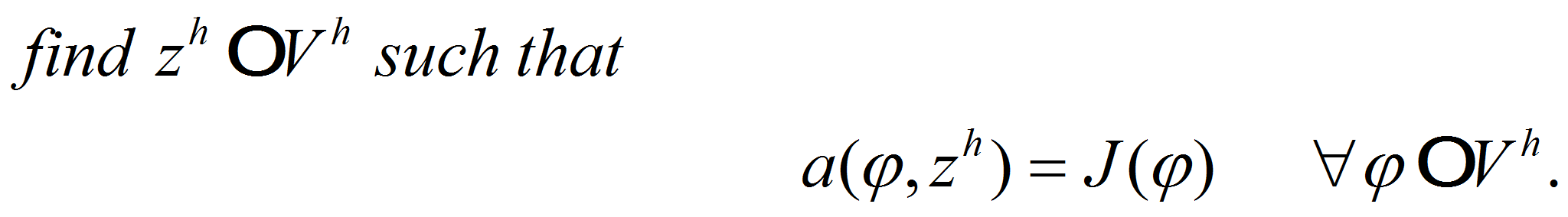I. Introduction
Traditional methods of solving equations of mathematical physics, such as finite element method, are to find a solution in the entire domain of definition. Corresponding methods of computational error analysis consist in defining the norm for difference between the exact and approximate solutions also in the whole domain. Meanwhile, in a number of applications, researchers are interested not in the solution as a whole, but only in its certain values or functionals named as goal-oriented or output ones. For example, in air flow around the body, engineers are interested in lift and drag, not in the solution at every point in space, especially away from the constructed body [1, 2]. In such cases, one would be interested in the calculation precision of these output functionals, and not of the entire solution. Moreover, with appropriate triangulation in the finite element method one can achieve a significant increase in the accuracy of the required functionals without increasing the computational time for the problem as a whole [2, 3].
One of the interesting tasks consists in computation of the solution values along the part of boundary with Neumann boundary condition. Such situation occurs when the flux (heat flux, for instance) at body surface equals to zero, and we need to know the resulting temperature at this surface.
In this article we consider a one-dimensional model problem with Neumann boundary condition at one of boundary points and try to find the solution value in the same point. For solving we use cubic Hermitian finite element method. Unexpectedly the ultrahigh order of convergence was obtained, which is not guaranteed by the finite element theory. Therefore the paper is devoted to the theoretical justification of this beneficial effect with the help of adjoint operators.
II. Formulations of problem
Consider one-dimensional model problem: find
![]() such that
such that
Functions
![]() are smooth enough for further considerations. Here and after any
constant
are smooth enough for further considerations. Here and after any
constant
![]() is supposed to be positive and independent of meshsizes
is supposed to be positive and independent of meshsizes
![]() Introduce the functional space
Introduce the functional space
![]() where last equality is valid in the sense of traces. We use the
standard notation for functional spaces that can be found for
instance in [4, 5].
where last equality is valid in the sense of traces. We use the
standard notation for functional spaces that can be found for
instance in [4, 5].
To get the weak form of this problem, multiply equation (1) by
arbitrary function
![]() and integrate by parts with the help of boundary conditions (2). As a
result we get the equalities
and integrate by parts with the help of boundary conditions (2). As a
result we get the equalities
In the weak form [4, 11] this problem is reformulated as follows:
Here and later
![]() is the bilinear form
is the bilinear form
![]() are scalar product and norm in space
are scalar product and norm in space
![]()
As it was mentioned above, in many real problems of mathematical physics the main important result is not the solution as a whole, but some its functionals. In this paper for above formulated problem we take the output functional
as an example and show that it is computed with better order of accuracy than the solution as a whole.
3. Finite element method with cubic Hermitian elements
First introduce mesh with nodes
![]() and notation
and notation
In accordance with handbooks [4, 11] introduce cubic basis functions of first type:
and second type:
Now introduce the finite element space
![]() consisting of piecewise polynomial functions of degree 3 as the
linear span of these basis functions:
consisting of piecewise polynomial functions of degree 3 as the
linear span of these basis functions:
Due to Galerkin approach we get the following formulation:
Owing to basis functions in
![]() we have decomposition
we have decomposition
with the vector of unknowns
where sign (…)T means transposition. This vector is found from the system of linear algebraic equations [6, 10]
where
![]() is
the global stiffness matrix and
is
the global stiffness matrix and![]() is
the global right-hand side.
is
the global right-hand side.
Introduce the error
![]() Subtracting (5) from (4) we get
Subtracting (5) from (4) we get
This property is well-known as Galerkin orthogonality property.
The accuracy of approximate solution is known from handbooks [4, 11]:
where
![]() means
the norms in the space
means
the norms in the space
![]() When
When
![]() we have the discrete imbedding (inverse) inequality [4, 5]
we have the discrete imbedding (inverse) inequality [4, 5]
Therefore we can guarantee only
4. A numerical result
Now consider the following concrete problem:
And then solve it by cubic finite element method that has been introduced before.
Table 1.
Numerical result for problem (11).
|
i |
h |
||
|
1 |
1/4 |
‒ 9.11 × 10-10 |
‒ |
|
3 |
1/8 |
‒1.75 × 10-11 |
5.72 |
|
5 |
1/16 |
‒3.03 × 10-13 |
5.87 |
From this Table we can see that
![]() tends to zero asymptotically as
tends to zero asymptotically as
![]() but not as
but not as
![]() or
or
![]() Is this result just a fortuity for this simple problem?
Is this result just a fortuity for this simple problem?
Now let us prove it for more general problems.
5. The proof of the higher convergence order for this type of output functional
Now introduce the following adjoint problem with the output
functional![]()
For smooth coefficients this weak formulation is equivalent to the following problem:
Its sufficiently smooth coefficients imply a sufficiently smooth solution. Like for the original problem (4), Galerkin approach in this case gives the following weak formulation:
Therefore, we get the discrete system for adjoint problem
with the same matrix
![]() due to symmetry of bilinear form:
due to symmetry of bilinear form:
![]() After solving this system the vector of unknowns
After solving this system the vector of unknowns
defines the approximate solution
Theorem. For sufficiently smooth data of problem (1)-(2) we get
Proof. From (12), (7), (13) we get
By standard way we get inequality
Since both problems have sufficiently smooth solutions, then
It implies that
Thus, we indeed get the sixth order of convergence for this output functional.
6. Resume
By virtue of the duality theory we prove the higher order of convergence than that is following from standard theory of Hermitian finite element method.
Note, that this effect became possible for cubic finite elements. For linear ones we should not get higher order of accuracy. Indeed, repeating this way of justification we should get only
It is not unusual for this type of elements for which we have typical estimate
References:
Shaydurov V., Liu T., Zheng Z.: Four-stage computational technology with adaptive numerical methods for computational aerodynamics. // American Institute of Physics. Conference Proceedings. 2012. – Vol. 1484. – P. 42-48.
ADIGMA.A European Initiative on the Development of Adaptive Higher-Order Variational Methods for Aerospace Applications. // Notes on Numerical Fluid Mechanics and Multidisciplinary Design. Vol. 113. - Berlin: Springer, 2010. – 498 p.
Bangerth W., Rannacher R.: Adaptive Finite Element Methods for Differential Equations. – Berlin: Birkhäuser, 2003. – 204 p.
Ciarlet P.G.: The Finite Element Method for Elliptic Problems. – New York: North Holland, 1978. – 530 p.
Сьярле Ф.: Метод конечных элементов для эллиптических задач. – М.: Мир, 1980. – 512 с.
Даутов Р.З., Карчевский М.М.: Ведение в теорию метода конечных элементов. – Казань: Казанский госуниверситет. – 2004. – 239 с.
Стренг Г., Фикс Дж.: Теория метода конечных элементов. – М.: Мир. – 1977. – 351 с.
Шайдуров В.В.: Многосеточные методы конечных элементов. – М.: Наука. – 1989. – 288 с.
Shaidurov V.: Multigrid Methods for Finite Elements. – Berlin: Springer. – 1995. – 300 p.
Strang G., Fix G.J.: An Analysis of the Finite Element Method. – New York: Prentice-Hall. – 1973. – 306 p.
Zhiming Chen, Haijun Wu: Selected Topics in Finite Element Methods. – Beijing: Science Press. – 2010. – 162 p.