В статье предложены математические модели, базирующиеся на вероятностном распределении основных параметров оперативного реагирования пожарно-спасательных подразделений.
Ключевые слова: математическая модель, эмпирическая вероятность, теоретическая вероятность, частота.
На сегодняшний день, оценка уровня оперативного реагирования пожарно-спасательных подразделений проводится путем анализа статистических показателей, зарегистрированных в ходе процесса пожаротушения, за определенный период времени.
По результатам вышеуказанных исследований формулируется вывод о необходимости совершенствования деятельности сил и средств пожарной охраны.
С целью упрощения проводимых оценочных процедур, а также для реализации возможности заблаговременного прогнозирования оперативной обстановки в районах выезда пожарно-спасательных частей и определения достаточности технического ресурса в штате подразделений предлагается применение следующих математических моделей поддержки принятия управленческих решений, базирующихся на статистическом аппарате данных:
— математическая модель определения частоты привлечения пожарной техники для обслуживания вызовов;
— модель динамики показателя вероятностного распределения числа вызовов в пожарно-спасательном гарнизоне по суткам;
— математическая модель распределения времени обслуживания вызовов;
— модель, определяющая критерий одновременной занятости пожарной техники обслуживанием выезда, связанным с пожаром.
Ознакомимся подробнее с сущностными характеристиками каждой из предложенных моделей, что, в свою очередь, позволит оценить эффект от их реализации.
Математическая модель определения частоты привлечения пожарной техники для обслуживания вызовов базируется на вероятностном распределении числа вызовов m i и количества привлекаемых для их обслуживания пожарных автомобилей i. За анализируемый период, как правило, принимается 365 дней, поскольку данный временной промежуток является показательным и позволяет детально отразить динамику исследуемых параметров [1].
Рассматриваемая модель включает в себя математические уравнения по определению абсолютных m i и относительных частот ω i привлечения технического ресурса пожарно-спасательных подразделений.
По результатам расчетов определяется средняя численность выезжающих на один вызов пожарных автомобилей:
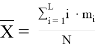
где
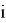
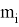

Таким образом, реализация предложенной математической модели позволяет определить фактически требуемое минимальное количество пожарных автомобилей в штате пожарно-спасательной части.
На основании проведенных расчетов должностные лица из числа руководящего состава подразделения могут принимать управленческие решения и формулировать предложения по осуществлению дополнительного комплектования ПСЧ пожарными автомобилями с целью повышения уровня оперативной готовности.
Сущность модели, характеризующей динамику показателя вероятностного распределения числа вызовов в пожарно-спасательном гарнизоне по суткам, заключается в определении эмпирической и теоретической вероятности привлечения подразделений пожарной охраны для проведения боевых действий по тушению пожаров за указанный промежуток времени [2].
Эмпирическая вероятность ω k того, что в интервале времени равным 1 суткам в городе произойдет k вызовов, оценивается как доля, которую в общем числе M суток составляет число суток, в течение которых произошло k вызовов:
|
|
(2) |
где

М — общее количество анализируемых суток, ед.
Теоретическая вероятность подчиняется закону распределения Пуассона и определяется следующим образом:

|
(3) |
где λ — плотность потока вызовов, т. е. среднее число вызовов, поступающих за единицу времени τ.
Резюмируя вышесказанное, стоит отметить, что полученные в ходе расчетов по данной модели результаты позволят оценить загруженность кадрового и технического ресурсов пожарно-спасательных подразделений и разработать концепцию по минимизации вероятности отказов в обслуживании вызова.
Математическая модель распределения времени обслуживания вызовов позволяет оценить длительность времени обслуживания τ обсл. m j -го количества вызовов, попадающих в j -й интервал времени [0,30], [30,60], [60,90], [90,120], [120, ∞].
В основе данной модели лежит следующее уравнение:
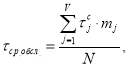
|
(4) |
где τ с j — середина j-ого интервала.
По результатам расчетных процедур выявляется среднее время обслуживания вызовов и интервал времени, характерные для подразделений, дислоцированных на территории исследуемого пожарно-спасательного гарнизона, что, в свою очередь, позволяет оценить уровень их оперативного реагирования и своевременно принять меры по его повышению.
В заключении данной научной статьи рассмотрим, предложенную автором математическую модель поддержки принятия управленческих решений, основанную на вероятностном распределении одновременной занятости пожарной техники обслуживанием вызовов.
С целью определения вероятности P k того, что в произвольный момент времени обслуживанием вызовов в городе будут одновременно заняты k пожарных автомобилей, используем следующие формулы:
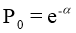
|
(5) |
|
|
(6) |
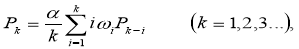
где α — приведенная плотность потока вызовов в городе, ед. [3];
τ ср.обсл. — длительность времени обслуживания, ч;
ω i — относительная частота привлечения i пожарных автомобилей для обслуживания вызовов, случае/ед. [4]
Таким образом, по результатам расчетов возможно получение эмпирических сведений о вероятности одновременной занятости пожарных автомобилей, суммарной продолжительности их обслуживания и частоте возникновения анализируемых ситуаций.
В завершении стоит отметить, что рассмотренные в ходе статьи модели направлены на детальное математическое моделирование процесса функционирования пожарно-спасательных подразделений и способствуют формированию достоверной оценки эффективности их деятельности.
Реализация предложенных моделей позволяет выработать заблаговременные управленческие решения по совершенствованию процесса выполнения основных оперативных задач караульной службы.
Литература:
1. С. Ю. Попков Методика оценки пожарных рисков в городах и сельской местности России: журнал «Технологии техносферной безопасности», выпуск № 5. — М.: Академия Государственной противопожарной службы МЧС России, 2012, — 11 с.
2. Гаврилей В. М., Панова Р. Г., Головина Г. Н. Классификация городов по пожарной опасности // Сб. «Проблемы пожарной безопасности объектов и административно-территориальных единиц».- М.:ВНИИПО, 2018, — 30 с.
3. Фирсов А. Г., Мешалкин Е. А., Порошин А. А. Зонирование территории Российской Федерации по показателям обстановки с пожарами с позиции климатических факторов // Пожарная безопасность, 2018, — 45 с.
4. Малько В. А. Модель и алгоритмы реорганизации региональной системы обеспечения пожарной безопасности на основе оценки пожарных рисков // Пожарная безопасность, 2020, — 2 с.








