В данной статье выполнен краткий обзор отечественных и зарубежных исследований, посвященных методам определения податливости узлов стальных конструкций, методикам расчета конструкций с учетом податливости узлов, способам моделирования узлов с учетом податливости. Целью будущего исследования является анализ изменений напряженно-деформированного состояния элементов конструкций высотного здания при учете податливости узлов аутригера. Моделирование и расчет конструкций будет производиться в программном комплексе ETABS и IDEA StatiCa. Результатом работы будет оценка влияния учета угловой податливости в узлах аутригерных конструкций при расчете высотных зданий на показатели напряженно-деформированного состояния элементов конструкций здания.
Ключевые слова: податливость узлов, узлы аутригерных конструкций, высотные здания, НДС узлов, полужесткие соединения.
На работу узлов металлических конструкций влияют множество факторов. Учет некоторых из них является трудоемкой задачей при проектировании. Среди таких факторов можно выделить податливость узлов, учет которой влияет на расчетные значения напряжений и деформаций элементов конструкции в целом.
Податливостью узла конструкции называется его способность приобретать угловые перемещения в результате деформативности элементов. Таким образом, жесткие соединения не являются абсолютно жесткими, так как воспринимают изгибающие моменты не в полной мере, а шарнирные в свою очередь воспринимают некоторую величину изгибающего момента.
Определение податливости узла, а также учет ее при выполнении расчета напряжений и деформаций элементов конструкции является трудоемкой задачей, однако в настоящее время существуют расчетные комплексы, которые значительно упрощают этот процесс. Это способствует получению более точной картины работы конструкции с меньшими трудозатратами.
Известно много исследований в данном направлении [1–20]. Прокомментируем некоторые из них.
В 1990 г. Колмогоровым Юрием Ивановичем был разработан экспериментально-теоретический метод определения податливости узлов для уточнения расчетных схем рам эксплуатируемых промзданий [1].
При помощи тензодатчиков нагружали опорную раму транспортной галереи и регистрировали изменения напряжений, а после разгрузки выполнлся контроль остаточных деформаций. Нагружали в несколько ступеней. Величина предварительной ступени достигала 2 кН, после чего сразу следовало измерение сопротивления тензодатчиками и отчет по измерительным приборам в таком состоянии принимался за условный ноль. Далее производили ступенчатое нагружение, на каждой ступени регистрировали изменения напряжений. Нагрузку увеличивали до тех пор, пока ее величина не достигала 28 кН. При такой нагрузке по расчету (без учета податливости) напряжения в наиболее нагруженных сечениях не должны превышать 30 МПа. Далее следовал очередной тест, в котором пробная нагрузка достигала своей предельной величины за 1 ступень.
По результатам тестовых испытаний были определены значения изгибающих моментов. Определение фактических характеристик податливости узлов опорной рамы транспортной галереи производилось по расчетным зависимостям, приведенным в тексте диссертации. Изгибающие моменты в верхнем и нижнем узлах стоек рамы были получены путем интерполяции и экстраполяции.
При сопоставлении значений изгибающих моментов, полученных при расчете без учета податливости и с учетом выявленной из тестовых испытаний податливости узлов обнаружена существенная разница расчетных усилий. В узлах сопряжения ригеля и стоек изгибающие моменты уменьшились в 1,73–1,89 раза от действия горизонтальной нагрузки. При действии распределенной по ригелю нагрузки изгибающие моменты в правом верхнем узле уменьшились на 4,3 %, а в левом увеличились на 1,1 %.
В 2014г в Приволжском научном журнале была опубликована статья, в которой проанализированы результаты численных и экспериментальных исследований стальных ферм из гнутых тонкостенных профилей на самонарезающих винтах и предложен алгоритм методики расчета таких конструкций с учетом податливости узловых соединений [2]. Авторы статьи: Лапшин, Морозов, Колесов.
В данном исследовании рассматривались фермы пролетами 3 и 6 м. Предварительно фермы были рассчитаны без учета податливости двумя способами:
1) линейный расчет по стержневой схеме;
2) нелинейный статический расчет с применением пластинчатых или объемных конечных элементов, при этом элементы фермы в узлах жестко соединены друг с другом (то есть без учета податливости).
Для учета податливости в расчетном комплексе «SCAD» был использован конечный элемент № 55, который предназначен для учета податливости материала между смежными узлами. Характеристиками упругой связи служат 6 коэффициентов упругости по трем осям, 3 — линейной упругости и 3 — угловой. Коэффициентом линейной упругости является отношение усилия к соответствующему ему перемещению.
Жесткость узловых соединений была установлена по результатам испытаний их полномасштабных соединений. Сечения элементов, метизы и их расположение были такие же, как в реальной конструкции. Для пролета 3м упругая стадия работы продолжалась до нагрузки 4 кН, для пролета 6м — 8 кН.
Для сравнения прогибов ферм были использованы результаты опытных исследований ферм пролетами 3 и 6 м, проведенных в 2013г в ННГАСУ [3].
По результатам испытаний и численных расчетов составлены сводные графики прогибов ферм пролетами 3 и 6м (рисунок 1 и 2). Из графиков видно, что результат расчета с учетом податливости дает лучшую сходимость с опытом.
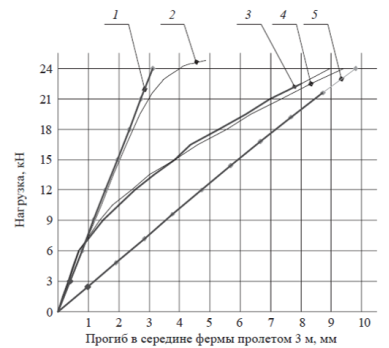
Рис. 1. Сводный графики зависимости вертикальных прогибов в середине фермы пролетом 3 м от нагрузки: 1 — Ф1, Ф2 численный линейный; 2 — Ф1, Ф2 численный нелинейный; 3 — Ф1 эксперимент; 4 — Ф2 эксперимент; 5 — Ф1, Ф2 нелинейный с учетом податливости
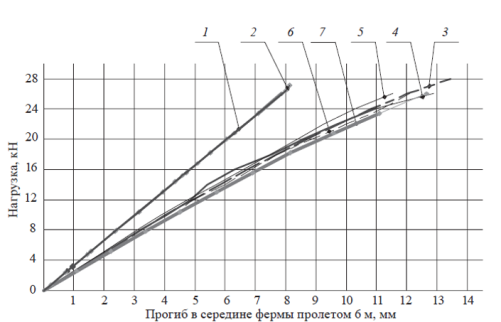
Рис. 2. Сводный графики зависимости вертикальных прогибов в середине фермы пролетом 6 м от нагрузки: 1 — Ф3-Ф6 численный линейный; 2 — Ф3-Ф6 численный нелинейный; 3 — Ф3 эксперимент; 4 — Ф4 эксперимент; 5 — Ф5 эксперимент; 6 — Ф6 эксперимент; 7 — Ф3–Ф6 нелинейный с учетом податливости
В 2017 г. в Сибирском государственном университете путей сообщения Новоселовым А. А. и Карелиным Д. А. была выполнена оценка влияния податливости опорного узла колонны на распределение усилий в элементах стального рамно-связевого каркаса [4].
Исследование проводилось на примере плоской рамы существующего 4-этажного общественного здания. Были подобраны сечения элементов каркаса по результату расчета на одновременное действие постоянной, временной и ветровой нагрузок. Затем были сконструированы опорные узлы.
Авторами предложена расчетная стержневая модель опорного узла, учитывающая податливость опорной плиты. Модель состоит из жесткой вставки бесконечно большой жесткости и двух изгибаемых стержней. Длина жесткой вставки принимается равной высоте колонны. Длины двух изгибаемых стержней равны расстоянию от грани колонны до центра анкерных болтов, а их жесткость соответствует жесткости опорной пластины. Концы изгибаемых стержней закреплены шарнирно. С учетом стержневой модели была выполнена корректировка расчетной схемы каркаса и выполнен перерасчет.
В результате было установлено, что учет податливости опорных узлов в плоском каркасе приводит к снижению опорных моментов на 0,5–10 %. Горизонтальные перемещения каркаса максимально увеличиваются в уровне перекрытия первого этажа на 4,2 %, при этом пролетные и узловые моменты балок максимально уменьшаются на 1 %.
В европейских нормах [5] учитывается влияние работы соединений на распределение внутренних сил и моментов в конструкции. Согласно п. 5.1.1 [5] — чтобы установить, должно ли в расчете учитываться влияние работы соединения на выполнение статического расчета различают три типа упрощенных моделей узлов:
– простой, в котором допускают, что узел не передает изгибающий момент;
– жесткий, в котором работа узла не влияет на результаты статического расчета;
– полужесткий, в котором следует учитывать влияние работы узла на статический расчет.
Выбор типа модели узла делается в зависимости от выбранного метода расчета и классификации узла по жесткости или по прочности.
В материале «Notes on Semi-Rigid Connections» [6] для моделирования полужестких соединений (semi-rigid connections) предлагается использовать поворотную пружину. Вращательная жесткость пружины k определяется отношением приложенного момента к значению угловой деформации соединения (рисунок 3). Значение вращательной жесткости могут быть определены экспериментальным путем.
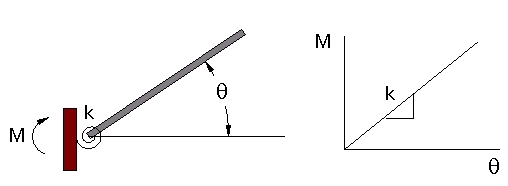
Рис. 3. Зависимость значения углового перемещения от момента
При этом значение вращательной жесткости не определяет, будет ли соединение жестким или шарнирным. Это отношение жесткости поворотной пружины к жесткости элемента при изгибе EI/L. Данное соотношение называется жесткостью соединения и определяется как kL/EI.
Для того, чтобы определить при каких значениях коэффициента жесткости соединения будут шарнирными, жесткими или полужесткими было исследовано динамическое и статическое поведение балки с равномерной нагрузкой.
Была создана конечно-элементная модель балки с пружинными шарнирами на опорах. Для получения минимальной собственной частоты для различных значений жесткости пружины k был выполнен анализ нормальных режимов NASTRAN. Результаты анализа приведены на рисунке 4.
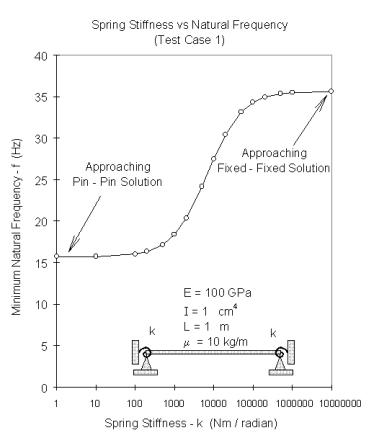
Рис. 4. Результаты анализа нормальных режимов NASTRAN модели балки с пружинными шарнирами
По мере уменьшения значения жесткости пружины решение узла приближается к шарнирному, в обратном случае — к жесткому. При этом существует некоторый диапазон, при котором узел считается полужестким.
Также было исследовано поведение другой балки с увеличенной массой, и балки с увеличенной жесткостью на изгиб. Результаты представлены на рисунке 5.
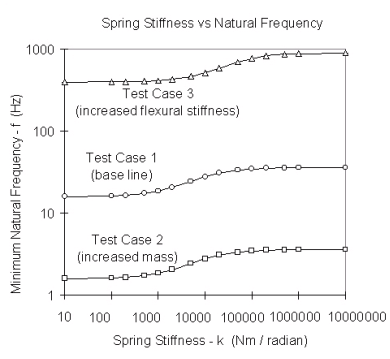
Рис. 5. Результаты анализа нормальных режимов NASTRAN моделей балок с увеличенной массой (2) и увеличенной жесткостью на изгиб (3) с пружинными шарнирами
При увеличении массы балки собственная частота колебаний уменьшилась, однако граничные значения диапазона перехода остались неизменными. При увеличении жесткости балки граничные значения диапазона смещаются. Таким образом жесткость балки на изгиб влияет на жесткость соединения.
В рамках данного анализа собственную частоту можно принять безразмерной. Значение собственной частоты, при которой решение узла является шарнирным, принято равным 0, а соответствующее жесткому узлу — 1. Вместо жесткости пружины использован коэффициент жесткости соединения k/EI/L. Зависимость, полученная таким образом, представлена на рисунке 6.
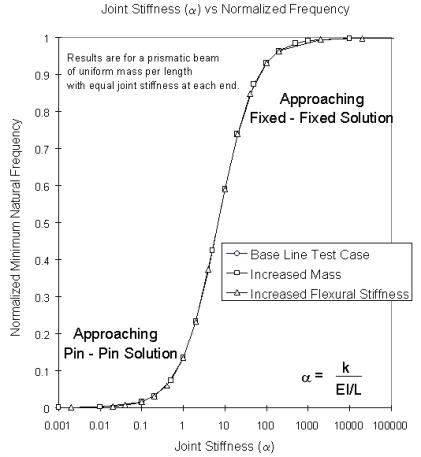
Рис. 6. График зависимости коэффициента жесткости соединения от собственной частоты колебаний
При анализе данной зависимости выявлено, что при значениях жесткости соединения, не превышающих 1, собственная частота находится в пределах 10 % от шарнирного решения узла, а при значениях жесткости соединения, превышающих 100, собственная частота находится в пределах 10 % от жесткого решения узла. При значениях жесткости соединения от 1 до 100 узел можно считать полужестким.
В статье «Effects of Semi-Rigid Connection on Structural Responses» [7] выполнено исследование работы рамы при изменении жесткости ее узлов от шарнирных до жестких с использованием программного комплекса ANSYS. Для моделирования полужестких соединений использовалась поворотная пружина.
Был выполнен статический расчет рамы с использованием поворотных пружин в опорных узлах. На рисунке 7 представлена расчетная схемы рамы с поворотными пружинами в опорных узлах.
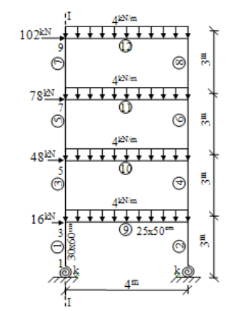
Рис. 7. Расчетная схема рамы с поворотными пружинами в опорных узлах
При моделировании работы поворотной пружины использовалась зависимость решения узла (в процентном соотношении от жесткого) от жесткости соединения (рисунок 8).
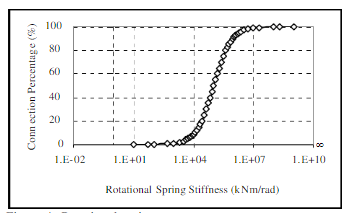
Рис. 8. Зависимость решения опорного узла (в процентном соотношении от жесткого) от жесткости соединения
Для различных решений узла получены эпюры усилий и перемещения в стойках рамы (рисунок 9 и 10).
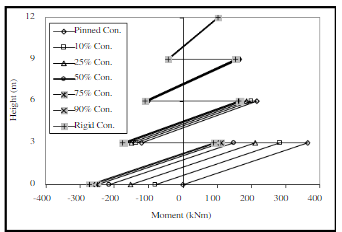
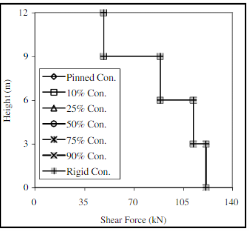
Рис. 9. Эпюры моментов (moment) и поперечной силы (shear force) в стойках рамы при различных решениях опорных узлов (pinned con. — шарнирный, rigid con. — жесткий, 10–90 % con. — полужесткий)
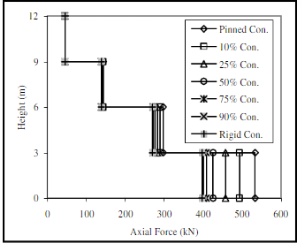
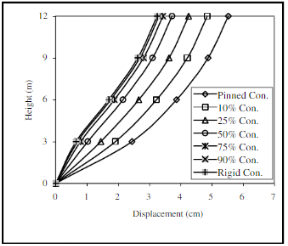
Рис. 10. Эпюры продольной силы (axial force), горизонтальные перемещения (displacement) в стойках рамы при различных решениях опорных узлов (pinned con. — шарнирный, rigid con. — жесткий, 10–90 % con. — полужесткий)
Аналогичный расчет был выполнен при использовании поворотной пружины в узлах сопряжения балок со стойками. Зависимость решения узла (в процентном соотношении от жесткого) от жесткости соединения для узла сопряжения балки со стойкой представлена на рисунке 11. Результат расчета представлен на рисунках 12 и 13.
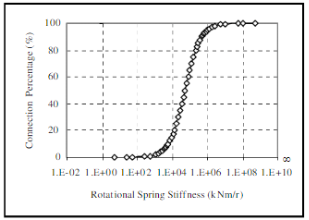
Рис. 11. Зависимость решения узла сопряжения балки со стойкой (в процентном соотношении от жесткого) от жесткости соединения
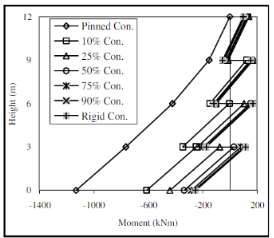
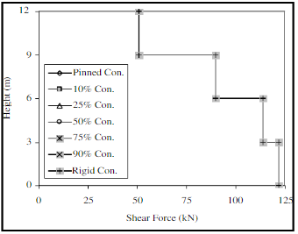
Рис. 12. Эпюры моментов (moment) и поперечной силы (shear force) в стойках рамы при различных решениях опорных узлов (pinned con. — шарнирный, rigid con. — жесткий, 10–90 % con. — полужесткий)
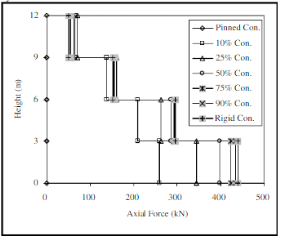
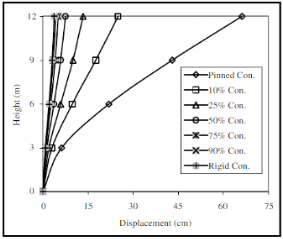
Рис. 13. Эпюры моментов (moment) и горизонтальные перемещения (displacement) в стойках рамы при различных решениях опорных узлов (pinned con. — шарнирный, rigid con. — жесткий, 10–90 % con. — полужесткий)
Таким образом, изменение жесткости узлов в разных узлах конструкции при статическом расчете может оказывать разное влияние на значения усилий в элементах расчетной схемы. В данном случае изменение жесткости узла сопряжения балки с колонной оказало большее влияние на усилия в элементах расчетной схемы, чем изменение жесткости в опорных узлах. При проектировании используя различные конструктивные исполнения узлов можно контролировать параметр жесткости узла, а соответственно и значения усилий в элементах конструкций.
В предстоящем исследовании будет рассмотрен вопрос учета податливости на примере конструктивной схемы высотного здания.
В книге [8] рассмотрены вопросы аутригерных конструкций высотных зданий и даны рекомендации к их проектированию. Считается, что в высотных зданиях этажностью свыше 50 этажей эффективность конструктивный системы повышается устройством в верху и посередине высоты здания аутригерных конструкций– горизонтальных поясов жесткости, включающих в работу ядра жесткости периметральные колонны каркаса. В таком случае изгибающий момент от ветровой нагрузки частично воспринимается ядром жесткости, частично — периметральными колоннами, которые препятствуют горизонтальному перемещению ядра и догружаются вертикальной нагрузкой от момента.
Наиболее сложными являются узлы сопряжения аутригерных конструкций (опоясывающих ферм, вертикальных связей и др.) с другими элементами каркаса. Обычно аутригер представляет собой систему перекрестных ферм в комбинации с опоясывающей фермой или иными несущими элементами. Для аутригерных конструкций характерно использование крупных сечений, поэтому в [8] рекомендуется производить расчет узлов с использованием конечно-элементных программных комплексов по деформированной схеме с учетом пластической работы материала. Однако, уточнение усилий в результате пластических деформаций узла не производится.
Целью будущей работы является оценка влияния податливости узлов аутригерных конструкций на распределение усилий в элементах каркаса высотных зданий, сравнение горизонтального перемещения верха здания, вычисленного без учета податливости с перемещением, вычисленным с учетом податливости.
Методы
Расчет стальных конструкций высотного здания будет выполнен с использованием программных комплексов, основанных на методе конечных элементов.
Работа будет выполняться в несколько этапов:
1) оценочный расчет с использованием программного комплекса ETABS, при котором определяются сечения элементов и конструктивные решения узлов, горизонтальное перемещение верха здания;
2) моделирование и расчет узлов аутригерных конструкций с учетом пластической работы материала с использованием программного комплекса IDEAStatiCa, определение угловой жесткости узлов;
3) статический расчет высотного здания с учетом полученной угловой жесткости узлов аутригерных конструкций.
Результаты
После выполнения расчетов и получения результатов будет произведено сравнение значений усилий и перемещений, полученных при расчете без учета податливости и с учетом податливости.
Обсуждение
Если при расчетах с учетом и без учета податливости возникнут значительные различия в значениях усилий и перемещений, то выводом исследования будет необходимость учета податливости при проектировании конструкций высотных зданий, а также дальнейшее развитие методов учета податливости при расчетах. В противном случае, учет податливости при расчете конструкций высотных зданий является нецелесообразным при проектировании, поскольку это потребует дополнительных затрат на проектирование и расчеты.
Выводы
По результатам исследования будут сделаны выводы о целесообразности учета податливости узлов аутригерных конструкций при проектировании высотных зданий.
Литература:
- Колмогоров Ю. И. Экспериментально-теоретический метод определения податливости узлов для уточнения расчетных схем рам эксплуатационных промзданий: дис. … канд. техн. наук: 05.23.01 / Колмогоров Юрий Иванович. — Ленинград.: ЛИСИ, 1990. — 185 с.
- Лапшин А. А. Методика проектирования стальных конструкций из гнутых тонкостенных профилей с учетом податливости узловых соединений на самонарезающих винтах / А. А. Лапшин, Д. В. Морозов, А. И. Колесов // Приволжский научных журнал. — 2014. — № 3 (31). — С. 16–25.
- Колесов А. И. Опытные исследования стальных ферм из тонкостенных холодногнутых профилей на самонарезающих винтах / А. И. Колесов, А. А. Лапшин, И. А. Ямбаев, Д. А. Морозов // Приволжский научный журнал. — 2013. — 4 (28). — С. 15–19.
- Новоселов А. А. Оценка влияния податливости опорного узла стальной колонны / А. А. Новоселов, Д. А. Карелин // Вестник Сибирского государственного университета путей сообщения. — 2017. — № 4 (43). — С. 26–31.
- EN 1993–1–8 (2005), Eurocode 3: Design of steel structures — Part 1–8: Design of joints. — URL: https://www.phd.eng.br/wp-content/uploads/2015/12/en.1993.1.8.2005–1.pdf
- Dr. John McGuire Notes on Semi-Rigid Connections [Электронный ресурс] / John McGuire. — URL: https://femci.gsfc.nasa.gov/semirigid/
- M. E. Kartal Effects of Semi-Rigid Connection on Structural Responses / M. E. Kartal, H. B. Başağa, A. Bayraktar, M. Muvafik // Electronic Journal of Structural Engineering. — 2010 — № 10. — С. 11–35.
- Ведяков И. И. Стальные конструкции высотных зданий / И. И. Ведяков, Д. В. Конин, П. Д. Одесский. — М.: Наука, 2014. — 272 с.
- Ананьин М. Ю. Метод учета податливости в узлах металлических конструкций зданий / М. Ю. Ананьин, Н. И. Фомин // Академический вестник УралНИИпроект РААСН. — 2010. — № 2. — С. 72–74.
- Бейсебаев А. К. Упругоподатливые соединения в элементах строительных конструкций // Современные аспекты совершенствования строительства: межвуз. сб. науч. тр. / Казахстанский политехн. ин-т. Алма-Ата, 1987.
- Горпинченко В. М. К вопросу расчета гибких соединений ригеля с колоннами / В. М. Горпинченко, Б. С. Цетлин, В. М. Туснина // Строительная механика и расчет сооружений. — 1989. — № 6. — С. 10–13.
- Марутян А. С. Учет влияния податливости узловых соединений перекрестных систем на работу конструкций покрытий / А. С. Марутян // Строительная механика и расчет сооружений. — 2008. № 6. — С. 2–6.
- Ольков Я. И. К уточнению расчетной схемы стальной рамы-этажерки / Я. И. Ольков, В. Н. Алехин // Известия вузов. Строительство и архитектура. — 1980. № 8.
- Рыпуло Ю. В. Напряженно-деформированное состояние каркасов сборно-разборных зданий с учетом нелинейно изменяющейся жесткости узловых соединений: дис. … канд. техн. наук: 05.23.01 / Рыпуло Юрий Викторович. — Киев.. НИИ строит. конструкций, 1991. — 16с.
- Троицкий П. Н. Исследование действительной работы сварного рамного узла крепления балок и рекомендации по их расчету / П. Н. Троицкий, И. В. Левитанский // Материалы по металлическим конструкциям. — 1977. Выпуск 19. — С. 120–132.
- Трофимов В. И. Учет влияния податливости болтового соединения на работу структурной конструкции / В. И. Трофимов, Э. В. Третьякова, И. И. Зуева // Строительная механика и расчет сооружений. — 1976. № 1. — С. 24–26.
- Фиш В. М. Определение моментов в продольных балках с учетом податливости прикреплений / В. М. Фиш, В. И. Клопотовский // Транспортное строительство. — 1984. № 12.
- Ackroyd M. H. Strength of Flexibity Connected Steel Frames / M. H. Ackroyd // Eng. Struct. — 1983. No. 1.
- Frye M. J. Analysis of Flexibly Connected Steel Frames / M. J. Frye, G. A. Morris // Canadian Journal of Civil Engineering. — 1975. 2. No. 3.
- Lindsey S. D. LRFD Analysis and Design of Beams with Partially Restrained Connections / S. D. Lindsey, S. A. Loannides, A. Goverdhan // Engineering Journal. — 1985. 22. No. 4.







