В работе авторы приводят краткую информацию об особенностях задачи с параметром в ЕГЭ по математике профильного уровня. Говорится об особенностях решения задач с параметрами разновидностями графического метода.
Ключевые слова: задача с параметром, графический метод.
Единый государственный экзамен (ЕГЭ) — это форма государственной итоговой аттестации (ГИА), ежегодное мероприятие, в котором участвуют сотни тысяч человек. ГИА проводится в целях определения соответствия результатов освоения обучающимися образовательных программ среднего общего образования соответствующим требованиям федерального государственного образовательного стандарта среднего общего образования (ФГОС СОО) [8]. С момента введения ЕГЭ в 2001 году поменялось многое: были введены многие предметы, формы экзаменов, структура экзаменов. Однако ЕГЭ по математике было с самого начала.
Традиционно КИМ ЕГЭ по математике профильного уровня содержит задания разного уровня сложности. Задание № 18 (№ 17 в 2022 году) — задание с параметром, относится к заданиям высокого уровня сложности. Для успешного выполнения задания с параметром необходим, кроме прочных математических знаний, также высокий уровень математической культуры, которая формируется в течение всего периода обучения на профильном уровне обучения математике. В 2022 году результаты решения задачи с параметром оказались выше, чем за предыдущие 8 лет (рисунок 1).
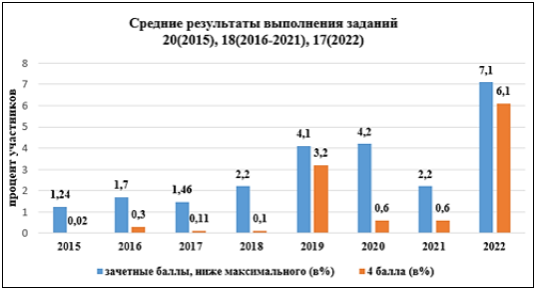
Рис. 1. Средние результаты выполнения задания
Рекомендацией статистико-аналитического отчета по результатам ЕГЭ является обучение обучающихся особенностям и методам решения задач с параметром.
В методических рекомендациях для председателей и членов предметных комиссий ЕГЭ есть информация о наиболее распространенных методах решения задачи с параметром на ЕГЭ по математике профильного уровня. Помимо алгебраического метода решения есть два других, один из которых основан на геометрических представлениях, а второй — на функциональных [4]. В тех же материалах приводится пример решения задания № 17 из демонстрационного варианта ЕГЭ 2023 года функционально-графическом методом.
Вопросами, касаемыми решение задач с параметрами занимались многие методисты, например, В. В. Амелькин, В. В. Мирошин, Е. М. Родионов, П. Ф. Севрюков, А. Х. Шахмейстер, П. И. Горнштейн, В. П. Моденов, О. Л. Безумова, С. Н. Котова, М. В. Шабанова, Г. А. Ястребинецкий, С. А. Шестаков и др. В методических разработках большинства этих авторов рассматривается большое многообразие методов решения задач с параметрами. Общей тенденцией является выделение методов, связанных с графическими представлениями, так называемых, графических методов решения задачи с параметром.
В методическое литературе встречаются и другие названия данного метода: метод выбора из графического представления множества решений [9], графический метод [1, 5] или прием [3], координатно-графический метод [5]. В. С. Высоцкий предлагает название «графический метод», который он делит на два подхода — метод сечений и координатно-параметрический [2].
Отметим, что в некоторой методической литературе графическим методом решения задач с параметрами так же называют функционально-графический метод решения задач с параметрами [1, 3, 5]. В этом методе параметр считается неравнозначным переменной. Путаница с методом выбора из графического представления множества решений возникает по причине того, что в обоих методах необходимо изобразить на координатной плоскости некоторое множество точек. Однако главным отличием функционально-графического метода является то, что в данном методе построение графического образа происходит в плоскости
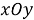
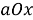
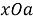
Таким образом, графический метод решения задач с параметрами — общее название для двух методов решения задач с параметрами — метода выбора из графического представления множества решений и функционально-графического метода решения задач с параметрами. Суть каждого из методов состоит в отображении множества точек на координатной плоскости. Различие методов состоит в выборе осей координат.
Метод выбора из графического представления множества решений заключается в том, что любую связанную пару переменной и параметра можно отметить, как координату точки плоскости. Тогда задачу с параметром можно переформулировать в задачу нахождения множества всех точек плоскости
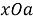
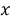
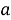
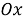
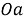
Главной особенностью функционально-графического метода является то, что параметр здесь является неравнозначным переменной. При отображении множества точек на координатной плоскости используется плоскость
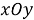
В современном процессе образования происходит развитие информационных технологий. Они находят свое применения в большинстве сфер жизни человека, в том числе и образовании. Для изучения и освоения некоторых тем школьного курса математики повышенной сложности возможно применение программного обеспечения, которое позволит сделать обучение более наглядным и доступным. Таким эффективным программным обеспечением можно считать интерактивные геометрические среды (ИГС). Вопросами применения ИГС в процессе обучения занимаются С. В. Ларин, В. Р. Майер, В. Н. Дубровский, В. Ненков, С. Гроздев, Т. Ф. Сергеева, Г. Б. Шабат, В. И. Рыжик, С. Г. Иванов, А. И. Сгибнев и др. Слово «геометрические» не обязывает учителей математики применять данный вид программ только на уроках геометрии. ИГС находят свое применение и на уроках математики и алгебры [7].
Яркими примерами систем динамической математики являются «Cabri Géomètre», «Geometer's Sketchpad» или «Живая математика», «GeoGebra», «Математический конструктор», «GEONExT». ИГС GeoGebra имеет на территории РФ широкое применение. Это ПО имеет открытый код, является общедоступным и свободно распространяемым, обладает простым интерфейсом пользователя, переведено на более, чем 40 языков мира. Соединение двух видов программного обеспечения — систем динамической геометрии и компьютерной алгебры, это отличительная особенность GeoGebra. Каждый объект в программе представлен не только в графическом виде, но и в аналитическом.
Приведем примеры решения задач, содержащих параметр, двумя разными видами графического метода.
Задание 1. Найти все значения параметра
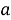
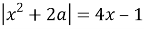
Решение.
Зададим две функции от левой и правой частей исходного уравнения:
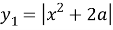
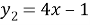
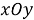
График линейной функции
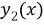
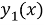
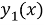
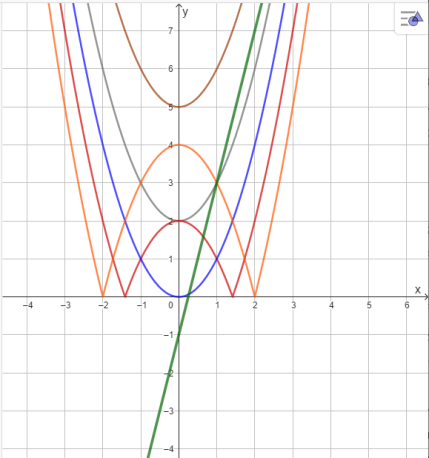
Рис. 2. Графики функций
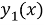
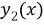
По графику видно, что «парабола» и прямая могут иметь разное количество общих точек: одну, две или не иметь общих точек вообще. Исходя из условий задачи, необходимо найти такое значение параметра, при котором графики не имеют общих точек. «Пограничное» расположение графиков — это когда прямая будет являться касательной для параболы, находящейся в верхней полуплоскости. То есть задача сводится к нахождению такого значения параметра, при котором график функции
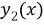
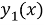
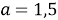
Если график функции
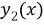
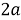
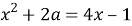
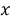
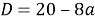
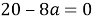
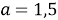
Обратимся к графикам функций. Если ордината вершины параболы будет принимать значения, меньше, чем 3, т. е.
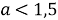
Ответ:
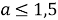
Решая задачу с параметрами функционально-графическим методом, чтение ответа происходит с графика. При этом у решающего могут возникнуть сложности или возможно допущение ошибки. В таком случае необходимо прибегнуть к аналитическому методу решения задач с параметрами для того, чтобы избежать трудностей и проверить достоверность считанных с графика данных.
Задание 2. Найдите значение параметра
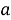
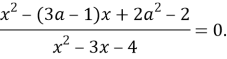
Решение.
Перепишем исходное уравнение в виде равносильной ему системы:
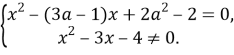
Рассмотрим отдельно каждую строчку системы.
Попробуем решить первое уравнение. Будем рассматривать квадратное уравнение относительно переменной
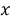
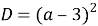
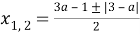
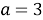
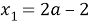
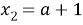
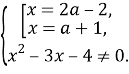
На данном этапе видно, что мы получили зависимость переменной
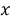
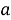
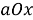
Решим неравенство
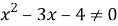
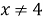
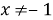
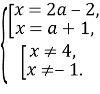
Отобразим множество точек, удовлетворяющих объединению совокупностей на координатной плоскости
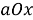
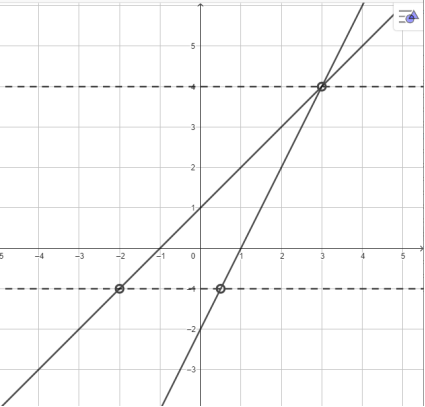
Рис. 3. Множество точек, удовлетворяющих системе
Из условия задачи делаем вывод, что необходимо найти такие значения параметра, при которых исходное уравнение имеет единственный корень, другими словами, вертикальная прямая имеет с двумя прямыми
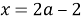
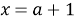
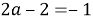
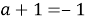
Ответ:
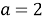
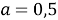
В процессе решения задачи методом выбора из графического представления множества решений, не всегда очевидно, какие именно точки необходимо отображать на плоскости. Здесь применим аналитический метод решения задачи с параметром, так как в ходе него исходное уравнение, неравенство или их система подвергаются равносильным преобразованиям. В ходе таких преобразований необходимо получить зависимость параметра от переменной (или наоборот).
Подводя итог всему вышесказанному, можно сказать, что графический метод решения задач с параметрами выделятся многими авторами и методистами наравне с другими различными методами решения задач с параметрами. Данный метод можно разбить на два метода, имеющих явные различия при их использовании: метод выбора из графического представления множества решений и функционально-графический метод решения задач с параметрами. Общая особенность каждого из методов — отображение множества точек на координатной плоскости. Различие — выбор осей координатной плоскости:
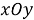
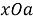
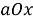
Литература:
- Амелькин, В. В. Задачи с параметрами: Справочное пособие по математике [Текст] / В. В. Амелькин, В. Л. Рабцевич. — Мн.: ООО «Асар», 2002. — 464 с.
- Высоцкий, В. С. Задачи с параметрами при подготовке к ЕГЭ [Текст] / В. С. Высоцкий. — Москва: Научный мир, 2011. — 316 с.
- Горнштейн, П. И. Задачи с параметрами. 3-е издание, дополненное и переработанное [Текст] / П. И. Горнштейн, В. Б. Полонский, М. С. Якир. — М.: Илекса, Харьков: Гимназия, 2005. — 328 с.
- Методические материалы для председателей и членов предметных комиссий субъектов Российской федерации по проверке выполнения заданий с развернутым ответом экзаменационных работ ЕГЭ 2023 года [Текст]: И. В. Ященко [и др.]; ФГБНУ «ФИПИ». — Москва:ФИПИ, 2023. — 114 с.
- Мирошин, В. В. Решение задач с параметрами. Теория и практика [Текст] / В. В. Мирошин. — М.: Издательство «Экзамен», 2009. — 286 с.
- Моденов, В. П. Задачи с параметрами. Координатно-параметрический метод [Текст]: учеб. пособ. / В. П. Моденов. — М.: Издательство «Экзамен», 2006. — 286 с.
- Павлова, М. А. Исследовательское обучение математике учащихся основной школы во внеурочное время с использованием систем динамической геометрии [Текст]: дисс. на соиск. учен. степ. канд. пед. наук: 13.00.02 / Павлова Мария Александровна; [Место защиты: ФГБОУ ВО «Елецкий государственный университет им. И. А. Бунина»]. — Архангельск, 2017. — 207 с.
- Российская Федерация. Порядок проведения государственной итоговой аттестации по образовательным программам среднего общего образования [Текст]: [Приказ Минпросвещения России, Рособрнадзора от 07.11.2018 г. № 190/1512]. — М.: Минпросвещения, 2018. — 58 с.
- Элективные математические курсы: Учеб. пособие [Текст] / М. В. Шабанова [и др.]. Поморский гос. ун-т им. М. В. Ломоносова. — Архангельск: Поморский университет, 2005. — 315 с.







