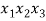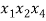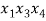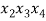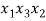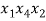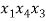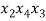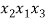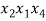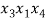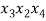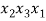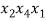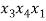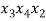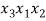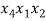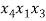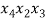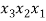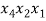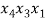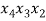Теоретический подход к решению комбинаторных задач



В статье рассмотрены основные понятия, встречающиеся при решении различных комбинаторных задач школьного курса математики.

Ключевые слова: комбинаторика, типы комбинаций.

В ряду всех наук математика занимает совершенно особое, принадлежащее лишь ей место. Естественные науки — физика, химия, астрономия, геология, минералогия изучают мир, в котором мы живем. Гуманитарные науки — лингвистика, литературоведение, юриспруденция (право), история, этика, социология — изучают человеческое общество в разных его проявлениях, то есть также нечто реально существующее, поддающееся наблюдению и даже эксперименту. В противоположность этому математика исследует некоторые абстрактные конструкции, вроде числа или линии, не имеющей ширины, а только длину; точнее всего объекты математики можно определить, указав, например, в геометрии, полный список аксиом, которым эти объекты должны удовлетворить. При этом выдающиеся роль математики связана с применимостью ее как естественным, так и гуманитарным наукам, с возможностью «математического моделирования» объектов реального мира.

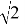
В технике, во многих науках, да и в обыденной жизни; бывают случаи, когда необходимо подсчитать число всех возможных вариантов, случаев, комбинаций и т. п. Раздел математики, изучающий методы решения подобных задач, называется комбинаторикой.

Методы, предлагаемые комбинаторикой, служат непосредственной основой для решения задач теории вероятностей, которая, как известно, играет основополагающую роль во многих отраслях знаний.

На протяжении длительного периода, комбинаторика, как самостоятельный раздел математики, преподавался лишь в классах с углубленным изучением математики, на факультативный занятиях. Однако значение комбинаторики отнюдь не пропорционально числу отводимых на нее часов. Комбинаторные задачи, имеют свою ярко выраженную специфику. Для них нет единого шаблона, каждая требует размышления, сообразительности, поисковой деятельности. Условия задач возникают, как правило, из жизненных ситуаций, и, значит, воспитывают умения переводить их на язык математики, т. е. стоить математические модели. А это одна из целей изучения математики.

Как показывает опыт, комбинаторные задачи способствуют развитию и помогают удовлетворению естественной любознательности детей, повышают интерес к математике. Комбинаторный подход дополняет логическое мышление его собственной формой — комбинаторным анализом.

Поэтому в обычных классах полезно с самых ранних ступеней обучения предлагать несложные задачи комбинированного содержания в качестве упражнений на развитие мышления и для возбуждения интереса. Решать их надо просто рассуждением. Нецелесообразно при первом знакомстве с комбинаторикой трактовать ее основные понятия как теоретико-множественные образования. Это полезно при обобщающем подходе, когда важно показать единство математики как науки, подчеркнуть возможность построения всех ее разделов с единых позиций. Но когда речь идет о том, чтобы понять, и главное, научиться применять комбинаторные понятия и зависимости, то теоретико-множественная модель оказывается лишним звеном на пути от конкретной задачи к ее математической сути. Поэтому различные типы комбинаций удобнее определять непосредственно по их свойствам [2].

Основные типы комбинаций — размещения и сочетания — вводятся не поочередно, а одновременно, путем параллельного сопоставления. Это дает возможность сразу подчеркнуть их различие и тем самым подготовить обучающегося к преодолению главной трудности — распознаванию типа комбинации в конкретных задачах. Этой же цели служит учебный алгоритм. Решение примеров начинается с рассмотрения задач, названных ключевыми, т. е. таких, методы решения которых могут быть применены во многих случаях. При этом для комбинаторики характерно, что задачи, схожие по методу решения, могут быть не похожими по их содержанию.

Основные типы комбинаций

Различные виды комбинаторных задач могут быть представлены такой схемой: имеется конечное множество, состоящее из n элементов: { , ,…, }; из этих элементов составляются комбинации, каждая из которых состоит из m элементов; нужно узнать, сколькими способами можно это сделать, т. е. сколько существует таких комбинаций. Ответ зависит от того, каковы условия составления комбинаций, которые определяются по смыслу конкретной задачи. Необходимо выяснить, могут ли среди элементов, составляющих одну комбинацию, быть одинаковые? В зависимости от ответа на этот вопрос получаем либо комбинации с повторяющимися элементами, либо комбинации без повторяющихся элементов, т. е. комбинации с повторениями комбинации без повторений [2].

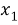
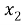
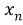
Например, если поставлен вопрос: «Сколько имеется пятизначных чисел?», то мы будем иметь дело с комбинациями, допускающими повторение элементов, так как одна и та же цифра может встретиться в записи числа несколько раз. А вот если требуется найти, сколькими способами можно избрать в президиум собрания трех человек из 20 присутствующих, то уже получаются комбинации без повторений, ибо каждый человек неповторим.

Далее, опять исходя из смысла задачи, нужно выяснить, имеет ли значение для данных комбинаций порядок элементов в каждой из них. Если образовать комбинацию в соответствии с условием задачи, а затем только поменять местами ее элементы, то получится новая комбинация, отличная от первоначальной, или же она, по существу, останется без изменения? Комбинации, которые меняются при изменении порядка элементов в них, называются размещениями. А комбинации, в которых порядок элементов роли не играет, называются сочетаниями.

Так, если изменить порядок цифр в записи числа, то получится другое число. Поэтому в приведенном выше примере о количестве всех пятизначных чисел, образующиеся комбинации (т. е. числа) следует отнести к размещениям.

А в задаче об избрании президиума нужно подсчитывать число сочетаний (из 20 элементов по 3), т. к. в данном случае существенно только то, кто будет избран в состав президиума, а в каком порядке будут названы фамилии — роли не играет.

(Другое дело, заметим в скобках, если бы при избрании указывались также обязанности членов президиума — председатель, секретарь, член президиума. В такой ситуации число возможных составов президиума надо было бы рассматривать как число размещений).

Из всего сказанного вытекает план дальнейшей работы: вывести формулы для подсчета числа размещений и числа сочетаний — без повторяющихся элементов и с повторениями. А затем надо будет рассмотреть приемы решения более сложных задач, в которых размещения и сочетания встречаются «не сами по себе», а в различных комбинациях.

Размещения

Размещениями называются такие комбинации, для которых имеет значение как то, из каких элементов они состоят, так и порядок элементов, что это значит, если в какой-либо комбинации заменить хотя бы один элемент или изменить порядок элементов, то получится новая комбинация, отличная от первоначальной.

Так, в задаче о количестве всех пятизначных чисел мы имеем дело с комбинациями из 10 элементов (цифр) по 5 элементов в каждой комбинации. Заменив хотя бы одну цифру или изменив порядок цифр, получим число, отличное от первоначально взятого.

Число размещений без повторения из n элементов по m в каждом обозначать . А для обозначения числа размещений с повторениями введем еще черточку сверху .

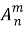
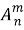
Сначала обратимся к рассмотрению размещений без повторяющихся элементов. В этом случае, число элементов в одной комбинации не может быть больше общего числа элементов в одной комбинации не может быть больше общего числа элементов в исходном множестве, т. е. .

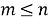
Рассмотрим процесс непосредственного составления размещений, а именно образуем все размещения без повторений из трех элементов по два.

Исходное множество: { ,

, }.

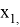
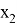
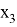
В качестве первого элемента можно выбрать любой из данных элементов, т. е. первый элемент можно выбрать тремя способами [3]. В качестве второго элемента можно к каждому из первых элементов присоединить любой из двух оставшихся (но не тот, который был выбран первым, так как в комбинациях не должно быть одинаковых элементов), рисунок 1.

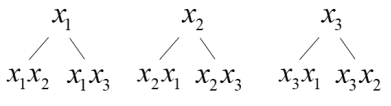
Рис. 1. Схема 1 составления размещений без повторений

Все полученные двухэлементные комбинации — это различные размещения, поскольку они отличаются друг от друга или элементами, или их порядком. Таким образом, каждый из трех первых элементов образует 2 размещения из 2 элементов. Значит, всех двухэлементных размещений будет .

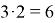
В общем случае имеем исходное множество: . Первый элемент можно выбрать n способами, после чего останется элементов, тогда второй элемент можно выбрать

способами, а всего двухэлементных размещений получится . После выбора второго элемента останется элементов. Значит, третий элемент можно присоединить к двум уже выбранным способами, а всех трехэлементных размещений будет . Закончится этот процесс выбором m-го элемента. Перед этим был выбран -й элемент, значит, осталось элементов, и последний, m-й элемент можно выбрать способами. А всех m-элементных размещений будет .

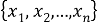
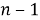
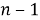
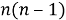
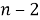
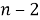
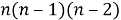
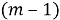
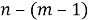
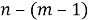
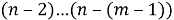
Число размещений без повторений из n элементов выражается формулой:

(1)

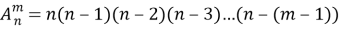
Полезно обратить внимание на то, что в правой части этой формулы имеется m множителей — столько, сколько элементов в одной комбинации, т. е. столько, каков верхний индекс в обозначении числа размещений. Поэтому удобно вычислять так: находим произведение, первый множитель которого — нижний индекс; каждый следующий множитель на единицу меньше предыдущего; и всех множителей столько, каков верхний индекс. Например, (размещений без повторяющихся элементов из 6 по 4).

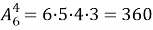
Если выражение (1) для числа размещений умножить и разделить на , то получим:

(2)

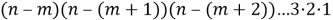
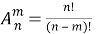
Для вычислений формула (2) менее удобна, но она полезна для изучения свойств размещений.

Теперь рассмотрим размещения, в которых возможно повторение элементов. Исходное множество снова . Каждая комбинация содержит m данных элементов, но так как допускается повторение, то m может быть и больше n.

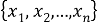
В качестве первого элемента одной комбинации можно взять любой элемент исходного множества, т. е. этот выбор можно сделать n способами [3]. Но так как элементы могут повторяться, то вторым элементом может быть выбран опять любой из n данных элементов, в том числе и тот, который был выбран первым. Точно также и выбор третьего элемента, и четвертого, и вообще каждого из m элементов, образующих одну комбинацию, можно сделать n способами. Схема 2, аналогичная схеме 1, для размещений с повторениями из 3 элементов по 2 будет выглядеть так (рисунок 2):

Рис. 2. Схема 2 составления размещений с повторениями

Отсюда . В общем случае:

(3)

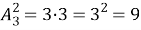
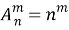
Для запоминания полезно обратить внимание на то, что в правой части формулы (3) буквы m и n расположены так же, как и в левой: m вверху, n внизу.

Перестановки

Важным частным случаем размещений являются перестановки. Перестановками называются комбинации, которые отличаются друг от друга только порядком элементов. Это возможно, что в каждую перестановку входят все наличные элементы. Иначе говоря, для перестановок . Так, например, в задаче: «Сколькими способами можно пересаживать 5 человек на 5 стульях?», мы имеем дело с перестановками (без повторяющихся элементов). Число перестановок без повторений из n элементов обозначается

. Так как для перестановок , то по формуле (1) получаем:

(4)

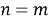
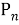
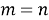
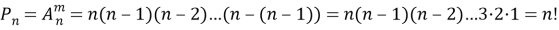
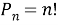
Значит, число возможных пересаживаний 5 человек на 5 стульях равняется .

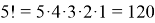
Перестановки с повторениями получаются, когда в исходном наборе элементов есть одинаковые элементы. Понятно, что число перестановок из n элементов, среди которых есть одинаковые, будет меньше, чем n!, так как если поменять местами два одинаковых элемента, то комбинация остается прежней.

Пусть мы хотим, например, подсчитать число перестановок из 5 элементов, один из которых повторяется 3 раза, т. е. исходный набор таков: . Если бы все элементы отличались друг от друга, то число перестановок равнялось

. На самом деле различных перестановок будет меньше за счет того, что среди этих 120 комбинаций встречаются одинаковые, а именно те, которые получатся, когда будут меняться местами только элементы . Значит, имеется 6 случаев, когда в перестановке меняются местами только элементы . Сама перестановка при этом не изменяется. Следовательно, комбинация среди всех перестановок из 5 элементов повторится 6 раз. То же самое можно сказать и о любой другой перестановке из трех элементов и элементов и : каждая будет повторяться 6 раз. Значит, всех различных перестановок будет не 120, а в 6 раз меньше, т. е. 20. Итак, число перестановок из 5 элементов, среди которых 3 одинаковых, равняется .

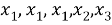
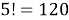
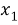
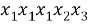
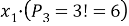
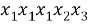
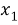
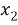
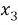
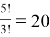
Если бы элементы и

также были одинаковы, т. е. рассматривались бы перестановки из трех элементов одного вида и двух элементов другого вида, то различных комбинаций было бы еще меньше — во столько раз, сколькими способами можно переставить 2 элемента на двух местах, т. е. в 2! раз. В такой ситуации число перестановок равнялось бы .

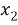
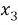
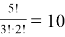
В общем случае пусть нам нужно найти число перестановок из n элементов, среди которых элементов первого вида, элементов второго вида ,…, элементов k-го вида, причем, конечно, + +…+ . Обозначим искомое число ( ,

,…, ). Прочесть этот символ можно так: «число перестановок с повторениями из n элементов с разбивкой , ,…, ». Поэтому, число перестановок с повторениями, равно:

(5)

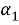
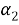
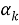
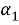
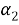
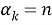
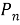
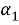
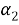
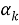
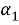
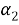
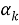
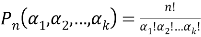
Сочетания

Сочетаниями называются такие комбинации, которые отличаются друг от друга хотя бы одним элементом; порядок элементов для них значения не имеет.

Так, в задаче об избрании в президиум (без распределения обязанностей) трех человек из 20 присутствующих образующиеся комбинации являются сочетаниями из 20 элементов из 3.

Число сочетаний без повторения из n элементов по m будем обозначать

, с повторяющимися элементами .

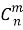
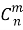
Чтобы лучше уяснить идею вывода формулы для ,возьмем в качестве примера исходное множество и образуем все сочетания без повторений из трех элементов. Это будут комбинации, которые будут отличаться хотя бы одним элементом. Их будет четыре: , , , .

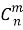
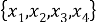
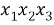
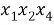
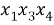
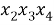
Теперь в каждом из этих сочетаний сделаем все возможные перестановки (таблица 1).

Таблица 1

В итоге получили все комбинации из 4 элементов по 3 без повторений, которые отличаются как элементами, так и их порядком, т. е. получили все размещения из 4 элементов по 3. Число их равно произведению числа строк данной таблицы на число ее столбцов. Но первая строка — это все сочетания из 4 элементов по 3, значит, столбцов в этой таблице столько, сколько таких сочетаний, т. е. число столбцов — это , а строк столько, сколькими способами можно переставить элементы в одном сочетании из трех элементов, т. е. число строк равно . Следовательно, число всех размещений , значит

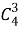
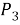
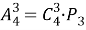
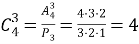
Аналогичным образом можно рассуждать и в общем случае для комбинаций без повторяющихся элементов: если в каждом сочетании из n элементов по m сделать все перестановки из m элементов, то получим все размещения из n по m элементов. Поэтому и с учетом формул (1) и (4) имеем:

(6)

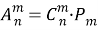
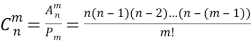
Если воспользоваться равенством (2) , то формулу (6) можно представить так:

(7)

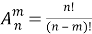
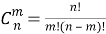
Из этого соотношения следует важное свойство сочетаний:

(8)

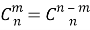
Это свойство, в частности, позволяет сократить выкладки для вычисления в тех случаях, когда m близко к n. Например,

.

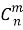
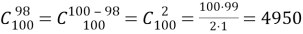
Без свойства (8) пришлось бы в числителе и знаменателе писать 98 множителей, а затем сократить 96 из них.

В случае, когда

сочетание имеется только одно — его образуют все данные элементы безотносительно к их порядку. Этот же результат дает формула (6): .

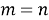
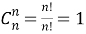
Но тогда целесообразно считать, что и выражение, получаемое для по формуле (7), тоже равно единице, т. е. считать, что . Чтобы это равенство имело смысл, . Рассмотрение сочетаний с повторяющимися элементами начнем с примера. Пусть имеются книги трех авторов скажем Дюма, Жюля Верна и Майн-Рида, и мы хотим подобрать из них подарок в пять книг. Сколькими способами можно это сделать, различая книги только по их авторам? Понятно, что в одном подарке могут оказаться книги одного и того же автора, т. е. элементы могут повторяться. Ясно и то, что порядок, в котором берутся книги, роли не играет. Важно лишь, сколько книг какого автора будет включено в подарок. Состав подарка можно обозначить так: сначала берем книги Дюма и напишем столько единиц, сколько книг взяли. Затем напишем нуль — знак разделения. Затем напишем столько единиц, сколько возьмем книг Жюля Верна и опять поставим нуль. Наконец, напишем столько единиц, сколько возьмем книг Майн-Рида. Например, взяв две книги Дюма, одну книгу Жюля Верна и две книги Майн-Рида (всех пять), обозначим этот выбор записью 1101011. Запись 1011101 означает, что выбраны одна книга Дюма, три книги Жюля Верна и одна книга Майн-Рида. Запись 1100111 соответствует подарку из двух книг Дюма и трех книг Майн-Рида; а если сделать подарок любителю только Жюля Верна, то получим запись 0111110. Отсюда вывод: сколько можно сделать подобных записей, столько можно образовать подарков. Но каждая такая запись есть комбинация из пяти единиц и двух нулей, которыми разделяются три группы единиц, соответствующих книгам трех авторов. Отличаются эти комбинации только порядком своих элементов. Значит. Их число можно найти как число перестановок с повторениями из 7 элементов с разбивкой 5 и 2. Отсюда .

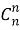
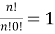
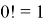
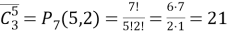
Легко видеть, что метод подсчета числа сочетаний с повторениями, может быть применен ко всем комбинациям, в котором порядок не существенен. Если нужно найти число сочетаний с повторениями из n элементов по m, то каждое такое сочетание можно изобразить как комбинацию из m единиц, разбитых на n групп, и нулей, разделяющих эти группы. Число таких комбинаций есть число перестановок с повторениями из элементов с разбивкой m и .

(9)

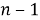
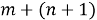
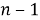
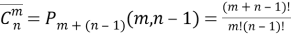
Заметим, что и воспользовавшись равенством можно правую часть формулы (9) представить как и таким путем прийти к соотношению между числом сочетаний с повторяющимися элементами и числом сочетаний без повторений:

(10)

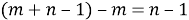
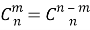
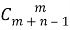
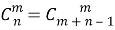
Литература:

1. Программы для общеобразовательных школ, гимназий, лицеев. Математика. 5–11 классы: Программы. Тематическое планирование. — М.: Дрофа, 2002.
2. Виленкин Н. В. Индукция. Комбинаторика. — М.: Просвещение, 1976.
3. Василенко Ю. К. Начала комбинаторики. Как преподавать их учащимся. — Белгород.: БелГУ, 1993.