Ключевые слова: многочлен, остаток, следствие, целый коэффициент, необходимое и достаточное условие, найти корень, наибольший общий делитель (НОД), алгоритм Евклида, делитель целого числа.
Keywords: polynom, residual, conslusion, integer, necessary and enough, search a root, greatest common divisor or highest common factor (GCD or HCF), factor of an integer, degree.
Понятие многочлена имеет значительное место в математике. В том числе понятие корень многочлена часто используется в алгебре и анализе. Формула нахождения корня многочлена для
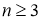
Пусть
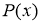
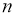
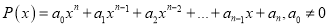
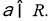
Теорема (Безу): Остаток
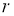
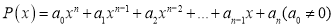
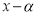
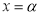
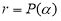
Следствие 1.
Для многочлена
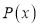
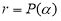
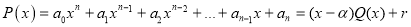
где
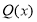
Некоторые применения теоремы Безу:
1. Нахождение корней многочлена
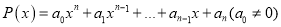
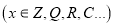
Обычно, если отношение свободного члена
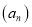
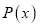
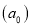
-
Сначала найдем целые делители главного коэффициента
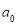
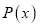
-
Числа, которые могут иметь рациональные корни:
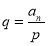
-
Проверяются всевозможные числа, т. е. должно выполняться условие
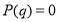
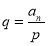
Задача 1. Найти корни многочлена с помощью теоремы Безу
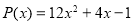
Решение:
Вданном примере главный коэффициент отличен от 1. Поэтому сначала проверяем:
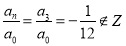
1. Найдем целые делители главного коэффициента
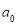
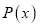
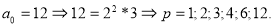
2.
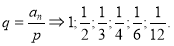
3.
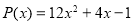
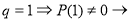
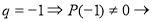
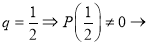
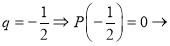
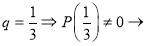
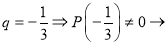
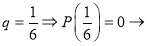
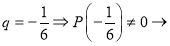
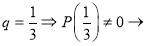
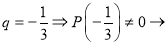
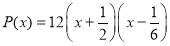
Ответ:
Данный многочлен
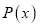
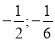
Задача 2
. Найти частное от деления многочлена
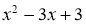
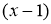
Решение:
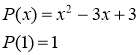
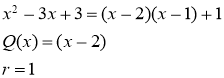
Задача 3.
Остаток от деления многочлена
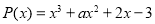
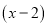
Остаток от деления многочлена
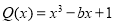
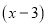
Остаток от деления многочлена
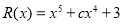
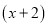
Найти остаток от деления многочлена
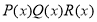
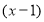
Решение.
Используя теорему Безу, запишем параметры
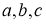
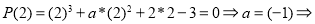

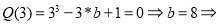
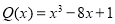
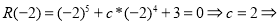
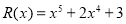
Согласно теореме Безу остаток от деления многочлена
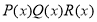
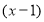
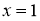
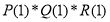
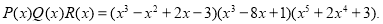
Следовательно
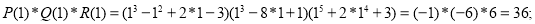
Задача 4. Найти число целых корней многочлена
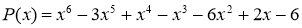
Решение:
Все решения ищутся среди делителей свободного члена согласно вышеизложенному. Тогда их легко проверить с помощью теоремы Безу:
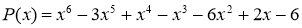
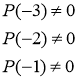
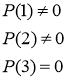
Следовательно по теореме Безу число 3 является единственным целым решением данного уравнения. В общем случае оно может быть кратным корнем.
По следствию теоремы Безу, если разделим данный многочлен на многочлен (x-3), то:
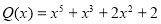
Снова используя теорему Безу, имеем
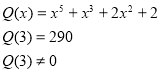
т. е. число 3 является корнем многочлена P(x).
Задача 4.
Существует ли многочлен
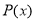
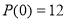
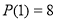
Решение.
Согласно теореме Безу остаток от деления многочлена
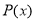
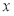
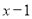
Пусть
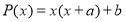
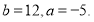
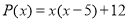
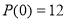
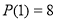
Ответ:
Да, существует. Например,
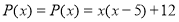
Задача 5. При каком значении параметра
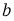
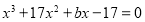
Решение.
Если ввести обозначение
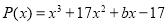
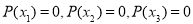
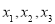
Для данной задачи решения должны быть целые числа. Поэтому мы находим целые делители свободного члена данного многочлена и проверяем, используя теорему Безу.
Здесь свободный член
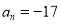
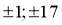
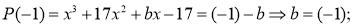
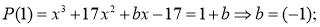
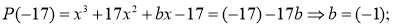
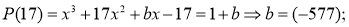
Здесь число 17 не является корнем. Потому что значение параметра
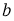
Замечание.
Уравнение не имело бы трех целочисленных решений, если бы количество значений, отличных друг от друга, было больше единицы, когда проверили возможные целые значения
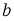
Следствие 2.
Напомним, что остаток от деления многочлена
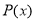
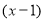
Сумму коэффициентов
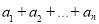
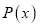
Задача 6.
Найти сумму коэффициентов многочлена
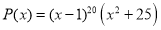
Решение.
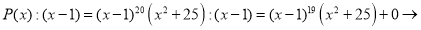
Данный многочлен делится на
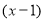
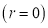
Литература:
- Andrzej Trybulec. On the sets inhabited by numbers. Formalized Mathematics, 11(4):341–347, 2003.
- Винберг Э. Б. Курс алгебры, — М.: Издательство «Факториал Пресс», 2002, ISBN 5–88688–060–7.
- Piotr Rudnicki (2004). «Little Bézout Theorem (Factor Theorem)" Formalized Mathematics. 12 (1): 49–58.







