В статье рассмотрены основные приемы решения элементарных и комбинированных комбинаторных задач.
Ключевые слова: комбинаторика, приемы решения.
Каждая комбинаторная задача индивидуальна, и не существует единого метода, пригодного для любой из них. Всегда приходится думать, искать пути решения. Вместе с тем многие задачи, хотя и отличаются по содержанию, сходны по подходу к их решению, позволяют использовать аналогичные приемы рассуждений. Это дает возможность обратить внимание на ряд типичных ситуаций, дать некий набор «ключей», которые можно попробовать, чтобы «открыть» задачу. Хотя, конечно, без гарантии успеха: к иной нешаблонной задаче может не подойти ни один ключ из имеющего набора, и придется «изготовлять» новый.
Задачи можно разделить на элементарные и комбинированные. Элементарные — это те, которые решаются в одно действие; для их решения достаточно подобрать соответствующую формулу и провести вычисления. В этих задачах самое главное — проанализировать условие и правильно определить тип комбинаций [2].
В комбинированных задачах размещения, перестановки, сочетания оказываются компонентами более сложных комбинаций. Обычный подход в комбинированных задачах — расчленить их на элементарные, найти ответ в каждой такой части, а затем искать способ подсчета тех более сложных комбинаций, которые отвечают условию задачи.
Принцип суммы и произведения
На заключительном этапе решения комбинаторных задач часто возникают следующие ситуации:
— для осуществления сложной комбинации нужно, чтобы имела место каждая из образующих ее элементарных ситуаций;
— для осуществления сложной комбинации достаточно, чтобы имела место хотя бы одна из образующих ее элементарных комбинаций.
Рассмотрим пример, который вместе с тем позволит обнаружить закономерности, возникающие в каждой из отмеченных ситуаций.
Имеются три яблока и две груши, причем каждый плод имеет свои отличия. Первый вопрос: сколькими способами можно выбрать яблоко и грушу? Второй вопрос: сколькими способами можно выбрать яблоко или грушу?
В первом случае рассуждаем так: поскольку очередность выбора значения не имеет, то предположим, что сначала выбираем яблоко. Это можно сделать тремя способами. К каждому из выбранных яблок можно присоединить любую из двух груш. Каждый выбор яблока приводит к образованию 2 пар «яблоко-груша», а таких выборов 3, значит, всех способов выбрать яблоко и грушу будет
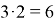
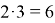
Во втором случае начинаем с того, что яблоко можно выбрать тремя способами, а грушу двумя. Но теперь нам нужно выбрать яблоко или грушу, т. е. один плод. Ясно, что способов это сделать будет
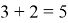
Аналогичные соображения позволяют в общем случае сформулировать правила, которые обычно называют принцип произведения и принцип суммы.
Принцип произведения:
если комбинацию А можно осуществить
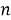
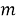
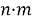
Действительно, в каждом из
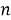
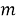
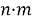
Полезны и другие формулировки принципа произведения:
— если выбор объекта А можно сделать
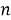
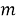
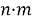
— если какой-либо объект А может находиться в
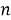
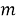
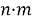
Ради простоты принцип произведения сформулирован для двух комбинаций (объектов), но ясно, что он справедлив и для любого их числа.
Принцип суммы:
если комбинацию А можно осуществить
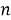
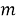
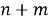
Важным частным случаем использования принципа суммы является применение его к так называемой «полной системе событий».
Если условию задачи удовлетворяет одно и только одно из событий
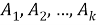
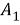
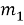
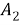

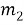
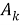
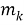
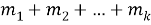
На рисунке 1 представлен учебный алгоритм для решения комбинаторных задач (рисунок 1) [1].
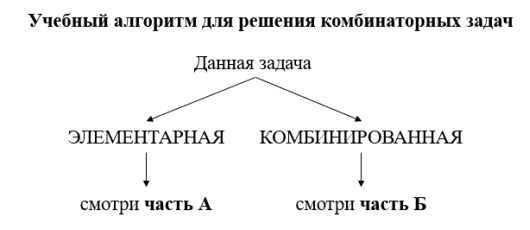
Рис. 1. Учебный алгоритм для решения комбинаторных задач
На рисунках 2 и 3 представлены алгоритмы решения элементарных и комбинированных задач.

Рис. 2. Алгоритм решения элементарных задач

Рис. 3. Алгоритм решения комбинированных задач
Типичный ход мысли в задачах по комбинаторике представлен в виде учебного алгоритма. Заметим при этом, что нашему мышлению свойственно как бы «проскакивать» отдельные этапы, получать выводы, не фиксируя каждый шаг поиска. Разумеется, это хорошо, но чтобы процесс мышления был осознанным и не свелся к действиям наугад, полезно, особенно, на первых порах, отдавать себе время от времени отчет, почему и как мы пришли к тому или иному заключению. Учебный алгоритм помогает организовать мышление, направить его в нужное русло, в случае необходимости внести коррективы. Таким путем учитель получает возможность в известной мере управлять процессом мышления учащегося в ходе его поисковой деятельности при решении комбинаторных задач.
Литература:
- Василенко Ю. К. Начала комбинаторики. Как преподавать их учащимся. — Белгород.: БелГУ, 1993.
- Виленкин Н. В. Индукция. Комбинаторика. — М.: Просвещение, 1976.







