Техника приближенных операций с комплексными числами в инженерной практике



В статье рассмотрены вопросы формирования навыков приближенных операций с комплексными числами в инженерной практике, а именно для оценки влияния комплексных компонент на тот или иной показатель решаемой инженерно-технической задачи. Приведены примеры приближенного выполнения элементарных операций с комплексными числами на основе приемов интерполяции и навыков устного счета в четырехзначном диапазоне. Предложена упрощенная форма записи комплексного числа в полярном виде без мнимой единицы для более наглядного представления числа в комплексной плоскости.

Представленная методика быстрых оценочных операций с комплексными числами может быть востребована при решении ряда инженерно-технически задач, где навыки операций с комплексными числами могут существенно сократить время обработки информации и повысить качество принимаемых решений. По мнению авторов, изложенный материал позволит студентам и даже школьникам старших классов глубже погрузиться в мир комплексных чисел, так как основан на приемах обычной арифметики и не использует сложных математических выкладок.

Ключевые слова : комплексные числа, мнимая единица, полярный вид, комплексная плоскость, устный счет, четырехзначная арифметика, линейная интерполяция, тригонометрические функции, приближенные вычисления, погрешность, калькулятор комплексных чисел.

Введение. Уникальные свойства комплексных чисел предоставляют широкие возможности для решения многих инженерных задач, однако на практике обычно используются лишь в качестве технического приема для упрощения математических преобразований. Конечный результат таких преобразований стараются снова перевести в вещественную форму. Экспериментальные (измеряемые) величины тоже представляются с помощью вещественной части. Мнимую часть либо отбрасывают, как ненаблюдаемую, либо вводят новую характеристику с ее представлением в вещественном виде. Между тем многие физические процессы лежат чисто в поле комплексных чисел (движение космических объектов, характеристики цепей переменного тока, навигация, теория колебаний, электромагнетизм, обработка сигналов, квантовые процессы и т. п.).

Сложившаяся практика во многом объясняется проблемами слабого среднего образования, где формируются базовые математические понятия [1]. В частности, из-за отсутствия навыков вычислительных операций с комплексными числами студентам технических вузов трудно дается такой раздел математики, как теория функций комплексных переменных, что негативно сказывается на качестве подготовки специалистов и подтверждает актуальность исследований техники операций в поле комплексных чисел.

Цель работы — сформулировать набор приемов, позволяющих устно, без калькулятора быстро производить приближенные операции в поле комплексных чисел, образующихся при измерении физических величин или при обработке экспериментальных данных.

В инженерной практике обычно не требуется высокой точности вычислений. Для принятия решений, в частности при вариантном проектировании, бывает достаточно результатов оценочных вычислений с двумя-тремя верными десятичными знаками. Опытные инженеры уверенно владеют техникой таких вычислений с действительными числами, чего нельзя сказать про комплексные числа. Предлагаемая техника базируется на гипотезе расширения навыков устной арифметики на поле комплексных чисел.

Общие положения. Комплексные числа (см. рис. 1) отличаются от обычных наличием мнимой части b , традиционно записываемой в виде произведения bi , где i — мнимая единица, численно равная i = . Комплексное число принято записывать в одной из трех форм [2]:

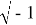
алгебраическая a + bi , (1)

тригонометрическая r ( cos φ + i sin φ) , (2)

показательная . (3)

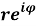
Тригонометрическая и показательная форма связаны между собой формулой Эйлера [2], = cos φ + i sin φ (4)

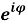
из которой следует известная формула Муавра для возведения в степень комплексных чисел z ⁿ = r ⁿ ⋅ [ cos (n φ ) + i sin (n φ )] (5)

В этих формулах a и b — соответственно действительная ( Re ) и мнимая ( Im ) часть комплексного числа; r = — модуль; φ — аргумент; e ≈ 2,71828 — число Эйлера (основание натурального логарифма).

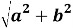
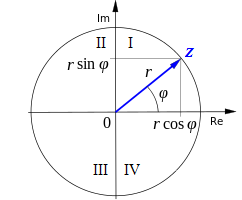
Рис. 1. Геометрическая интерпретация комплексного числа

Формулы (1–4) наиболее востребованы при математическом моделировании, поскольку существенно облегчают решение различных уравнений в комплексной области, однако довольно сложны для восприятия не только школьникам, но и зачастую студентам младших курсов по целому ряду причин. В частности, термин « мнимый » ассоциируется как нереальный, т. е. лишенный всяческого смысла; мнимую единицу i часто путают с силой тока в физике или с переменной цикла в информатике. Сложилось устойчивое восприятие комплексного числа как «пары действительных чисел, взятых в определенном порядке» — такое определение можно увидеть в весьма уважаемых пособиях по теории функций комплексной переменной, например, [3]. Заметим, что комплексное число является именно одним числом [2], а не алгебраической парой или произведением модуля на аргумент, как это представляется из формул (1–4). Ведь запись вещественного числа 7,75 в алгебраической форме 7 применяют лишь в исключительных случаях, чтобы подчеркнуть, что это число точное, а не приближенное. Цифры после десятичной запятой как бы уточняют число 7 на величину 0,75. Нам представляется логичным использовать этот же прием и для записи комплексного числа в полярном виде [4], отделяя апострофом[1] аргумент комплексного числа в градусной мере:

≡ r ’φ

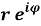
Упростив запись, мы как бы подчеркиваем сущность комплексного числа именно как единого числа, а не формы его математического представления. Например, в записи 7,75’38 ⁰ значение 38 ⁰ после апострофа уточняет положение числа Z на комплексной плоскости (см. рис. 1). При необходимости комплексное число, записанное в полярном виде, по формулам (1–4) легко преобразуется в любую из трех принятых форм.

Сразу обратим внимание, что комплексное число в полярном виде всегда положительно. Знак минуса перед таким числом не имеет смысла, т. к. модуль r всегда положителен по определению. Во избежание путаницы также условимся задавать аргумент φ положительным значением угла против часовой стрелки в диапазоне от 0 ⁰ до 360 ⁰ . Например, отрицательному действительному числу -7,75 эквивалентно комплексное число в полярном виде 7,75’180 ⁰ . Таким образом в комплексной плоскости все отрицательные числа — суть положительные, но противоположного направления.

Преобразование чисел и приемы устных операций. Приближенные значения модуля и аргумента комплексного числа из его алгебраической формы можно получить с помощью теоремы Пифагора и тригонометрических функций . Для этого вполне подойдет техника приближенных вычислений с действительными числами [5], основанная на приемах устных операций и интерполяции в диапазоне четырехзначной арифметики.

1. Четырехзначная арифметика

Упрощение вычислений достигается применением следующих формул:

а) произведение одинаковых чисел (возведение в квадрат):

a ² = ( a + c ) ∙ ( a - c ) + c ²

б) произведение разных чисел:

a ∙ b = ( a + c )∙ b — c ∙ b

a ∙ b = ( a - c )∙ b + c ∙ b

Число с выбирается таким образом, чтобы полученная сумма ( a + c ) или разность ( a - c ) было числом, удобным для получения произведения или возведения в квадрат с точностью до 4-х знаков.

2. Интерполяционная решетка

Приближенный результат Y обратных операций (деление и извлечение корня) удобно находить линейной интерполяцией внутри заранее подобранного интервала ( x ₂ ; x ₁ ) с известными граничными значениями функции ( y ₂ ; y ₁ ), см. рис. 2а, б. Иногда вместо вычислений проще подобрать или «угадать» результат Y в интервале значений функции ( y ₂ ; y ₁ ) по «интерполяционной решетке» (см. рис. 2в, предложена М. Нартовой [5, с. 3]). При интерполировании в границах четырехзначной арифметики следует стремиться к тому, чтобы целочисленные значения границ интервала y ₂ - y ₁ отличались друг от друга на одну единицу, что упростит вычисления и снизит погрешность.

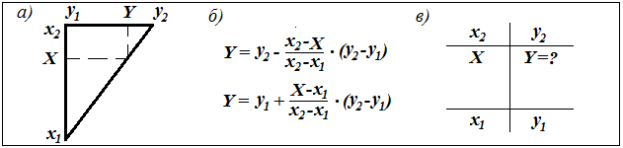
Рис. 2. Схема интерполяции

а) треугольник подобия; б) рабочие формулы; в) интерполяционная решётка

3. Тригонометрические функции

Тригонометрические функции удобно находить, мысленно представляя перед собой изображение тригонометрического круга и помня значения синуса и тангенса для углов через каждые 15 ⁰ (рис. 3).

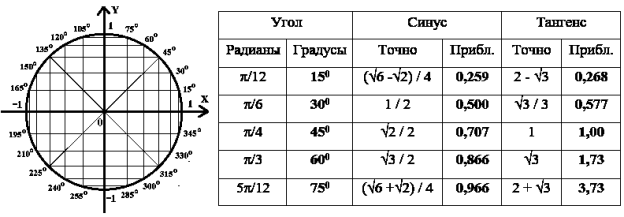
Рис. 3. Тригонометрический круг и значения функций через 15 ^о

Значения синуса и тангенса для промежуточных углов определяются интерполяцией. Тангенс угла более 45 ⁰ и синус угла более 60 ⁰ следует находить с учетом нелинейности (выпуклости) функций.

Приближенно синус малого угла (< 10 ⁰ ) примерно равен его тангенсу и самому углу в радианах — погрешность не превышает 1 %.

Формулы для повышения точности нахождения тангенса при α > 45 ⁰ :

ctg a = ; arctg a = arcctg .

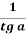
Формулы для повышения точности нахождения синуса и косинуса для углов, близких 0 ⁰ или к 90 ⁰ :

cos a = ; sin a = .

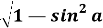
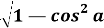
Приближенная формула А. Рыбака [8, с. 54], устанавливающая связь между константами e и π :

π ⁴ + π ⁵ = e ⁶

Пример 1. Покажем ход устных рассуждений (с фиксацией промежуточных результатов) при преобразовании комплексного числа 6,11 + 4,77 i в полярный вид:

6,11 ² ≈ 10– ² ∙ 61 ² = 10– ² ∙ (50∙72 + 11 ² = 3600 + 121 = 3721) ≈ 37,21

4,77 ² ≈ 10– ² ∙ 48 ² = 10– ² ∙ (50∙46 + 2 ² = 2300 + 4 = 2304) ≈ 23,04

r = ( = 7,7; =7,8) ≈ 7,75

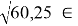
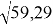
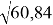
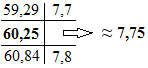
tg φ = 4,77/6,11 ≈ 10– ² ∙(4770/61 78; 80) ≈ 0,782 (I кв.)

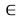
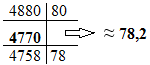
φ = arctg 0,782 (30 ⁰ ; 45 ⁰ ) ≈ 37,5 ⁰

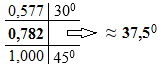
Ответ[2]: 6,11 + 4,77 i ≈ 7,75’37,5 ⁰ / 0,0 %; 0 ⁰

Пример 2. Преобразуем число (- 6,11–4,77 i ) с помощью тригонометрических функций. Внимательно следим за знаками согласно рис.1.

tg φ = (-4,77)/(-6,11) ≈ 0,782 (III кв.) φ =180 ⁰ + arctg 0,782

(30 ⁰ ; 45 ⁰ ) ≈ 217,5 ⁰

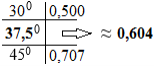
sin 217,5 ⁰ = - sin 37,5 ⁰ (-0,5; -0,707) ≈ - 0,604

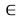
r = (-4,77)/(-0,604) ≈ 10– ¹ ∙ (4770/60,4 ≈ 60,4∙79/60,4 ≈ 79) ≈ 7,9

Ответ: - 6,11–4,77 i ≈ 7,9’217,5 ⁰ / 1,9 %; 0 ⁰

Как видно из примера 2, применение двойной интерполяции по тригонометрическим функциям вместо теоремы Пифагора увеличило погрешность нахождения модуля почти на 2 %.

Пример 3. Обратное преобразование числа 14’337,5 ⁰ .

Re. cos 337,5 ⁰ ∙ 14 = sin 67,5 ⁰ ∙ 14 ≈ 0,92 ∙ 14 ≈ 12,9 (IV кв),

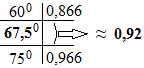
учтена выпуклость функции sin для угла больше 60 ⁰ .

Im. sin 337,5 ⁰ ∙ 14 = — sin 22,5 ⁰ ∙ 14 ≈ - 0,38 ∙ 14 ≈ -5,32

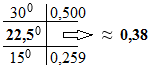
Ответ: 14’337,5 ⁰ ≈ 12,9–5,32 i / -0,3 %; -0,7 %

Сложение и вычитание. При сложении/вычитании комплексных чисел соответственно складываются/вычитаются их алгебраические компоненты . Неудобство таких операций с числами в полярном виде заключается в необходимости перевода исходных значений в алгебраическую форму и обратное преобразование результата сложения/вычитания компонент.

Пример 4. Найти разность комплексных чисел 14’337,5 ⁰ и 7,75’37,5 ⁰ .

С учетом ранее сделанных преобразований (см. примеры 1, 3), и не загромождая текст интерполяционными решетками, запишем:

14’337,5 ^0– 7,75’37,5 ⁰ = (12,9–5,32i) — (6,11 + 4,77i) = 6,79–10,09i (IV кв)

6,79 ² ≈ 7,0 ∙ 6,6 + 0,2 ² ≈ 39,64; 10,09 ² ≈ 10 ∙ 10,18 + 0,09 ² ≈ 101,81

r = = ( = 11; = 12) ≈ 11,9

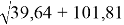
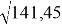
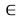
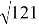
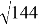
tg φ = (-10,09)/(+6,79) ≈ 10– ¹ ∙ (-1009/68 -15; -14) ≈ - 1,48

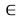
φ = arctg (-1,48) (360 ^0– 45 ⁰ ; 360 ^0– 60 ⁰ ) ≈ 360 ^0– 55 ⁰ ≈ 305 ⁰

Ответ[3]: 14’337,5 ^0– 7,75’37,5 ⁰ ≈ 11,9’305 ⁰ / -2 %; 1,0 ⁰

Задача 1. Катер, имея запас топлива 140 л., вышел из Тамани в Ейск маршрутом: 12 км по азимуту 315 ⁰ , 180 км — азимут 28 ⁰ , 42 км — азимут 90 ⁰ . Катер имеет на борту радиостанцию с дальностью уверенного приема 200 км. Определить риск потери связи с Таманью на маршруте и запас топлива при среднем расходе 50 л на 100 км пути.

Решение. Запишем маршрут в комплексных числах, совместив ось Re с направлением на Север с учетом того, что угол азимута измеряется по часовой стрелке, а аргумент φ — против: 12’45 ⁰ ; 180’332 ⁰ ; 42’270 ⁰ . Для того, чтобы просуммировать данные числа, переведем их в алгебраическую форму:

12’45 ⁰ = 12 (cos 45 ⁰ + i sin 45 ⁰ ) ≈ 12 (0,707 + i 0,707) ≈ 8,5 + 8,5i

180’332 ⁰ ≈ 180 (cos -28 ⁰ + i sin -28 ⁰ ) ≈ 180 (0,89 — i 0,47) ≈ 160–85i

42’270 ⁰ ≈ 42 (cos -90 ⁰ + i sin -90 ⁰ ) ≈ 42 (0,0 — i 1,0) ≈ 0–42i

12’45 ⁰ + 180’332 ⁰ + 42’270 ⁰ ≈ 168,5–118,5 i ≈ 170–120 i;

r : = ( = 200; = 210) ≈ 207

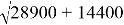
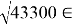
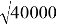
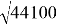
tg φ = (-120)/(+170) ≈ 10– ² ∙ (1200/17 70; 71) ≈ — 0,705

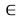
φ = arctg (-0,705) (-30 ⁰ ; -45 ⁰ ) + 360 ⁰ ≈ -35 ⁰ + 360 ⁰ ≈ 325 ⁰

12 ’45 ⁰ + 180 ’332 ⁰ + 42 ’270 ⁰ ≈ 170–120 i ≈ 207’325 ⁰ / 0,5 %; 0,2 ⁰

Ответ: Запас топлива: 140–50 ∙ (12+180+42) = 140–117 = 23 л ( 15 %).

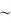
На последнем этапе маршрута имеется риск потери связи с Таманью (превышение дальности на 3,5 %, 207 > 200 км). Антенну радиостанции следует настроить на азимут 215 ⁰ ( φ = 325 ⁰ ), ориентир — ЮЮЗ.

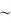
Умножение и деление. При умножении/делении комплексных чисел ум ножаются/делятся их модули и складываются/вычитаются аргументы .

Пример 5. 14’202,5 ⁰ ∙ 7,75’37,5 ⁰ = (14 ∙ 7,75)’(202,5 + 37,5) ⁰ = 108,5’240 ⁰

Пример 6. 14’202,5 ⁰ / 7,75’37,5 ⁰ = (14 / 7,75)’(202,5–37,5) ⁰ ≈ 1,80’165 ⁰

Пример 7. 108,5’240 ⁰ ∙ 1,80’165 ⁰ = (108,5 ∙ 1,8)’(240 + 165) ⁰ ≈

≈ (110∙1,8–1,5∙1,8)’(405–360) ⁰ ≈ 195’45 ⁰ / -0,2 %; 0 ⁰

Задача 2. Электродвигатель подключен по схеме «звезда» (см. рис. 4а) к трехфазной сети переменного тока частотой f = 50 Гц и напряжением 380 В. Определить активную мощность Р, потребляемую электродвигателем, если при активном сопротивлении каждой обмотки R = 20 Ом её индуктивность составляет L = 0,045 Гн.

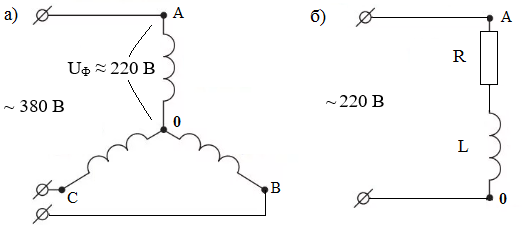
Рис. 4. Подключение трехфазного двигателя к сети 380 В

а) схема «звезда»; б) схема электрической цепи обмотки

Решение . В силу симметрии нагрузки обмоток по схеме «звезда» проведем расчет для одной обмотки. Электрическую цепь обмотки А можно представить в виде последовательного соединения активного сопротивления R = 20 Ом и индуктивности L = 0,045 Гн (рис. 4б).

Действующее фазовое напряжение: U _A = ∙ 380 ≈ 220 В.

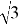
Комплексное сопротивление обмотки Z [6, с. 231]складывается из активного сопротивления R = 20 Ом и индуктивного (мнимого) R _L = 2π∙f∙L = 2π∙ 50∙0,045 ≈ 14,1 Ом. Преобразуем число Z = 20 + 14,1 i в полярный вид:

r = ≈ ( = 24; =25) ≈ 24,5

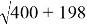
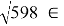
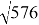
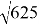
tg φ = 14,1/20 = 0,705 ;

φ = arctg 0,705 ( arctg 0,577 ≈ 30 ⁰ ; arctg 1 = 45 ⁰ ) ≈ 35 ⁰

Z = 20 + 14,1 i ≈ 24,5’35 ⁰

Ток I _A = U _A / Z = 220’0 ⁰ / 24,5’35 ⁰ = (220/24,5)’(0 ^0– 35 ⁰ +360 ⁰ ) ≈ 9,0’325 ⁰

Комплексная мощность S _A = U _A ∙I _A = 220’0 ⁰ ∙ 9,0’325 ⁰ = 1980’325 ⁰

Активная мощность, потребляемая тремя обмотками электродвигателя:

P = 3∙|S _A |∙ cos φ ≈ 3∙1980 ∙ cos 325 ⁰ ≈ 5940 ∙ sin 55 ⁰

sin 55 ⁰ ( sin 45 ⁰ ≈ 0,707; sin 60 ⁰ ≈ 0,866) ≈ 0,82

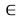
P ≈ 5940 ∙ 0,82 ≈ (5940–0,18∙5940) ≈ 4870 Вт / 0,6 %

Ответ: Активная потребляемая мощность P ≈ 4,87 кВт, коэффициент мощности (косинус угла сдвига между током и напряжением) cos 35 ⁰ ≈ 0,82.

Возведение в степень. Потребность в осмыслении комплексных чисел возникает еще в школе на этапе знакомства с графиками степенной функции, см. рис. 5).

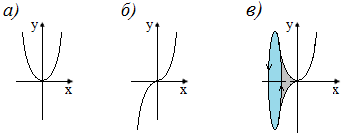
Рис. 5. Графики степенной функции

а) параболы четной степени, б) параболы нечетной степени; в) трансформация парабол при изменении четности степени

У школьников возникает вопрос, почему при переходе к нечетной степени (рис. 5 а, б) левая ветвь параболы скачком перемещается в нижнюю полуплоскость, и как будет выглядеть график при промежуточном значении показателя степени? Ответить на этот вопрос, не затрагивая понятие комплексных чисел, весьма затруднительно. Хотя на самом деле ответ очень прост. При плавном переходе, например, от квадратичной параболы к параболе 4-й степени левая ветвь совершает полный оборот в комплексной плоскости Re-Im (схематично — см. рис. 5 в), перпендикулярной плоскости x-y .

Такое наглядное пояснение расширяет пытливому школьнику путь в мир комплексных чисел. Трансформацию параболы рассмотрим подробнее на графике функции y = x ⁿ в диапазоне изменения x от -1,2 до +1,2 и n от 2 до 4.

Для наглядности (см. рис. 6) ось y совместим с осью Re . Произведя необходимые вычисления[4], результат отобразим в виде двух проекций: в плоскости действительных чисел ( n = 2; 7/3; 3; 4 — рис. 6а) и в комплексной плоскости (x = 0,75; 1,0; 1,2 при 2 ≤ n ≤ 4 — рис. 6б). На рис. 6 видно, что результату возведения числа -1,2 в степень 7/3 соответствует комплексное число Z = (-1,2) ^7/3 ≈ 0,77–1,33 i ≈ 1,53’60 ⁰ , расположенное на левой ветви параболы под углом 60 ⁰ к плоскости действительных чисел. Причем модуль числа r = 1,53 в точности соответствует результату возведения положительного числа 1,2 в степень 7/3.

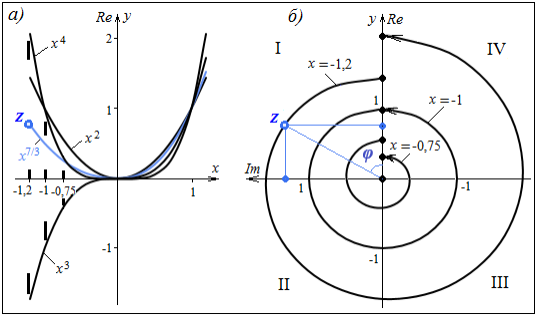
Рис. 6. Вращение левой ветви параболы

а) в действительной плоскости; б) в комплексной плоскости

Однако вернемся к вопросу техники приближенного возведения комплексных чисел в вещественную степень. С учетом введенных ранее ограничений для представления приближенных комплексных чисел в полярном виде (модуль — рациональное число r > 0, аргумент — угол в градусах 0 < φ < 360 ⁰ ), из формулы Муавра (5) следует, что для возведения в степень комплексного числа, нужно отдельно возвести в степень модуль исходного числа, а его аргумент умножить на показатель степени .

Пример 8. Покажем ход устных рассуждений на примере приближенного возведения комплексного числа 1,2’180 ⁰ (эквивалентно отрицательному числу -1,2) в степень 2,33. Поскольку 1,2 ² = 1,44; 1,2 ³ = 1,728, то линейная интерполяция дает результат r = 1,2 ^2,33 ≈ 1,54. Вычислим аргумент: 180 ⁰ ∙ 2,33 ≈ 420 ⁰ , т. е. с учетом вышеупомянутых ограничений φ ≈ 420 ^0– 360 ⁰ ≈ 60 ⁰ .

Окончательно: ( 1,2’180 ⁰ ) ^2,33 ≈ 1,54’60 ⁰ / -1,5 %; 0,6 ⁰

Пример 9. Возвести комплексное число 7,75’37,5 ⁰ встепень 1/3. Если показатель степени n < 1, то в результате нужно учесть столько значений произведений показателя степени n на расширенный аргумент φ + k ∙ 360 ⁰ , сколько помещается в интервале 0 < φ < 360 ⁰ , начиная с k=0 . В нашем случае:

1) (7,75’37,5 ⁰ ) ^(1/3) = (7,75 ^1/3 )’(37,5 ⁰ /3+0∙360 ⁰ /3) ≈ 2’12,5 ⁰ ; / 1,1 %; 0 ⁰

2) (7,75’37,5 ⁰ ) ^(1/3) = (7,75 ^1/3 )’(37,5 ⁰ /3+1∙360 ⁰ /3) ≈ 2’132,5 ⁰ ; / 1,1 %; 0 ⁰

3) (7,75’37,5 ⁰ ) ^(1/3) = (7,75 ^1/3 )’(37,5 ⁰ /3+2∙360 ⁰ /3) ≈ 2’252,5 ⁰ ; / 1,1 %; 0 ⁰

Пример 10. (7,75’37,5 ⁰ ) ^0,1 = (7,75 ^0,1 )’(0,1∙37,5 ⁰ + 0,1∙k∙360 ⁰ ) ≈

1) 1,2’3,75 ⁰ ; 2) 1,2’39,75 ⁰ ; 3) 1,2’75,75 ⁰ ; 4) 1,2’111,75 ⁰ ; 5) 1,2’147,75 ⁰ ;

6) 1,2’183,75 ⁰ ; 7) 1,2’219,75 ⁰ ; 8) 1,2’255,75 ⁰ ; 9) 1,2’291,75 ⁰ ; 10) 1,2’327,75 ⁰ .

В данном примере мы имеем десять приближенных решений, причем в качестве 1-го и 6-го можно ориентироваться на действительные числа +1,2 = 1,2’0 ⁰ и -1,2 = 1,2’180 ⁰ , т. к. относительная погрешность вычисления аргумента (1,0 %) в этих случаях не превышает погрешности вычисления модуля (-2,2 %).

Комплексный калькулятор. Показанныевыше приемы вычислительных операций с комплексными числами хороши для приближенных оценочных вычислений, т. к. позволяют избежать грубых ошибок. Для применения в инженерной практике хотелось бы иметь удобный калькулятор комплексных чисел. В ходе настоящей работы опробовано несколько различных калькуляторов. Общим недостатком просмотренных калькуляторов, затрудняющим их практическое применение, является их ориентация на представление комплексных чисел в стандартных формах — см. формулы (1–3). Такое представление влечет за собой необходимость выбора специального интерфейса, отличного от интерфейса стандартного калькулятора. Так, например, калькулятор [7] очень удобен для математических операций с комплексными числами, но трудоемок для инженерных вычислений, где доля операций с комплексными числами невелика. Поэтому в данной работе пришлось остановить свой выбор на программе Microsoft Excel, что также неудобно из-за двухкомпонентного представления чисел в алгебраическая форме.

От этих недостатков можно уйти, если оперировать с комплексным числом в полярном виде, как с одним числом. Используя интерфейс стандартного калькулятора, к десятичному числу можно добавить аргумент φ в градусах после повторного ввода десятичной запятой, которая отобразится на экране особым символом, например, апострофом — признаком аргумента.

В инженерной практике в основном нам приходится работать с приближенными числами, поэтому предлагается указывать аргумент φ в градусной мере. Благодаря этому будет соблюдаться условие кратности между φ и полным углом в 360 ⁰ , позволяющее избежать многозначности корней степенных уравнений, связанной с иррациональностью аргумента при его представлении в радианной мере.

На рис. 7 показан внешний вид (прототип) такого калькулятора, на основе поставляемого компанией Xiaomi Communications Co. Ltd в составе смартфонов Redmi. Исходное значение аргумента φ = 60 ^о указано после повторного нажатия клавиши десятичной запятой. На экране зафиксирован результат сложения единицы с комплексным числом 1,5’60 ^o , путем последовательного нажатия интуитивно понятных клавиш 1+1,5,60=. Заметим, что для выполнения данной операции на калькуляторе [7] необходимо ввести более сложную конструкцию вида 1+1,5*(cos(π/3)+i sin(π/3)).

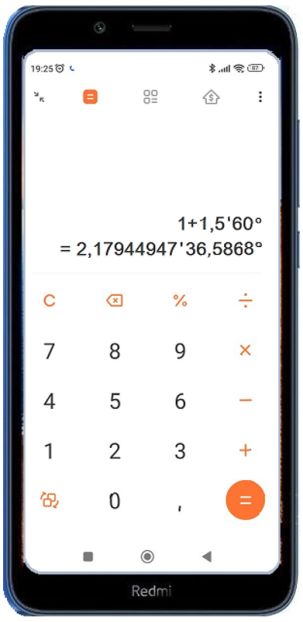
Рис. 7. Комплексный калькулятор

Заключение. Врезультате проделанной работы можно отметить, что:

— Вычислительные приемы на основе навыков четырёхзначной арифметики и линейной интерполяции, изложенные в [5], могут быть успешно применены и для приближенных (оценочных) операций с комплексными числами.

— Представление комплексных чисел в полярном виде очень удобно в инженерной практике благодаря очевидной связи с физическими процессами через соответствующие производные от модуля и аргумента: линейная и угловая скорость, ускорение, инерция, мощность и другие.

— Приближенные, в том числе устные операции с комплексными числами более сложны по сравнению с аналогичными операциями в поле действительных чисел вследствие роста вычислительной цепочки. Если в операциях умножения/деления или возведения в степень комплексных чисел усложнение и рост погрешности незначителен, то ручные операции сложения/вычитания в полярном виде достаточно громоздки, поскольку предполагают преобразование чисел из тригонометрической формы (полярного вида) в алгебраическую и наоборот.

— Предложенный способ представления комплексных чисел в полярном виде позволит использовать интерфейс стандартного калькулятора для операций с действительными и комплексными числами в привычной среде для широкого круга пользователей.

Отметим, что все вычислительные приемы, представленные в настоящей работе, в принципе не выходят за рамки школьной программы и доступны к освоению в инженерной практике.

Литература:

1. Виноградова Ю. А., Господинова А. Г., Иванова О. К., Яновская Е. А. Повышение уровня математического образования школьников, как основа развивающего пространства технологического университета. // Наука и образование: Новое время, 2016. — № 5. — стр. 208–214.
2. Комплексное число. Материал из Википедии — свободной энциклопедии. — URL: https://ru.wikipedia.org/wiki/Комплексное_число.
3. Терещенко А. М. Теория функций комплексной переменной: Учебное пособие. — М.: МИЭТ, 2006. — 123 с.
4. Polar Form and Rectangular Form Notation for Complex Numbers — URL: https://www.allaboutcircuits.com/textbook/alternating-current/chpt-2/polar-rectangular-notation (дата обращения: 10.07.2023).
5. Порядин А. И., Техника приближенных вычислений при решении инженерных и экономических задач / Порядин А. И., Красовская М. С., Нартова М. А., Трубникова М. А. // Молодой ученый, — 2021. — № 29 (371). — стр. 1–10. — URL: https://moluch.ru/archive/371/83230.
6. Теоретические основы электротехники: Учебник для вузов. Том 1. — 4-е изд. / К. С. Демирчян, Л. Р. Нейман, Н. В. Коровкин, В. Л. Чечурин. — СПб.: Питер, 2003.— 463 с.
7. Калькулятор комплексных чисел. Вычисление выражений с комплексными числами. — URL: https://programforyou.ru/calculators/complex-calculator (дата обращения: 10.07.2023).
8. Соловьев Ю. П. Комплексные числа. // Квант, 1991. — № 7. — стр. 47–54. — URL: https://kvant.ras.ru/1991/07/kompleksnye_chisla.htm.

---

[1] Применяется в MS Excel в качестве признака комплексного числа

[2] Здесь и далее после косой черты (/) указана относительная погрешность вычисления по модулю в процентах и абсолютная погрешность по аргументу в градусах

[3] При работе с тригонометрическими функциями нужно внимательно следить за положением числа на комплексной плоскости

[4] Вычислено с помощью MS Excel