В статье описаны результаты создания онлайн-помощника, посредством которого обучающиеся смогут строить графики функций, изучать их свойства, генерировать задания на сравнение выражений на основе монотонности, определять роль функций в окружающем мире.
Ключевые слова: функция, аргумент, система программирования, элементарные математические функции, график функции, свойства функций.
При изучении различных явлений человек имеет дело с переменными величинами, которые связаны между собой так, что значения одних независимых переменных определяют значения других зависимых переменных или функций. Ни один процесс в окружающем мире не может быть изучен без математического описания, в том числе, с помощью функций и их свойств, что необходимо для понимания их сути, предсказания хода развития и управления ими.
Инструментом для реализации авторского проекта выбрана система программирования Microsoft Visual Basic, так как является мощным средством разработки разнообразных приложений, баз данных, программ, работающих под управлением операционных систем семейства Microsoft Windows [1].
В математике функция — это зависимость между двумя множествами x и y, по которой каждому элементу х из множества Х соответствует единственный элемент у из множества Y. При этом переменную x называют независимой переменной или аргумент, а переменную у — зависимой переменной или функцией [2]. Множество точек плоскости, координаты которых удовлетворяют условию ( x , f ( x )), называется графиком функции y = f ( x ). Графическое представление функции удобно для непосредственного восприятия ее особенностей, описания свойств [2].
Среди всего многообразия функций выделяются функции, отличающиеся своей простотой и наиболее широкой областью применения. Это простейшие элементарные функции, основное значение которых состоит в том, что они составляют базу для изучения более сложных функций, являясь в большинстве своем составными элементами последних. Знание основных элементарных функций, их свойств и графиков не менее важно, чем знание таблицы умножения. Они как фундамент, на них все основано, из них все строится и к ним все сводится [2].
В проекте представлены функции: степенная, показательная, логарифмическая, тригонометрические и обратные тригонометрические. Выбор конкретной функции осуществляется с помощью элемента CheckBox. Для изучения выбранной функции в текстовое поле нужно ввести конкретное значение, щелкнуть по кнопке Функция, в окне PictureBox появится изображение графика, в таблице MSFlexGrid отобразятся свойства функции, в других двух таблицах сгенерируются задания на сравнение выражений, и в элементе RichTextBox выведется информация о применении соответствующих функций.
Например, степенная функция y =x n , где nR. При этом в зависимости от n рассматриваются различные виды степенной функции (Рис. 1).
Для каждого вида функции представлена информация о применении в окружающей действительности. Приведем примеры применения для степенной функции.
- Линейная функция . Длина l тела рассматривается как линейная функция его температуры: l(t)=l0(1+t) . Равномерное движение точки S ( t )= vt + S 0 . Зависимость расстояния на местности от расстояния на карте (масштабирование) S=10000К. Зависимость длины окружности от её радиуса. Плотность нефти от температуры, стоимость товара от количества и др. [5, 7].
- Гипербола. Выигрыш в силе, получаемый с помощью рычага, определяется отношением плеч приложенных сил. Во сколько раз выигрываешь в силе, во столько раз проигрываешь в расстоянии [2].
- Гиперболические навигационные системы. Штурман на борту самолёта или морского судна принимал радиосигналы от двух пар станций на берегу. Используя разность времени между моментами приема сигналов от обеих станций, штурман строил две гиперболы, пересечение которых на карте позволяло определить место, где он находился. Зависимость между объемом инвестиций и ставкой процента. Гиперболоид вращения (Шуховские башни) [5, 7].
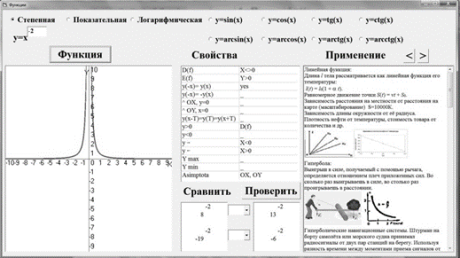
Рис. 1. Степенная функция
- Парабола. Траектория камня, брошенного под углом к горизонту, мяча, струи воды, выпущенной из шланга, парашютиста, выпрыгнувшего из горизонтально летящего самолета, артиллерийского снаряда, это парабола [5, 7].
Свойство параболических зеркал используют при конструировании солнечных печей, солнечных электростанций, отражательных телескопов — рефлекторов, прожекторов или фар автомобилей [5, 7].
В архитектуре и технике, например, параболическая антенна, свод моста, арка.
-
Зависимость интенсивности основного обмена от веса животного
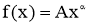
- График таяния льда при комнатной температуре. С мороза в комнату внесли банку со льдом. С течение времени температура таяния льда, а затем нагревания воды изменяется по законам степенной функции [5,7].
- Обратно пропорциональная квадратичная функция у=х-2 описывает процесс затухания волн и ослабления сил в зависимости от расстояния. Например, так затихает звук по мере удаления от источника [7].
- Инженер, производя расчеты на прочность, имеет дело с четвертыми степенями, и даже с шестыми степенями (например, при вычислении диаметра паропровода [6].
- Гидротехник при исследовании сил, с которой текучая вода увлекает камни, также встречается с функцией шестой степени: если скорость течения в одной реке в четыре раза больше, чем в другой, то быстрая река способна перекатывать по своему ложу камни в 46 раза более тяжелые, чем медленная [6].
- Общая яркость раскаленного тела — например, нити накала в электрической лампочке от температуры, растет при белом калении с двенадцатой степенью температуры, а при красном — с тридцатой степенью температуры [6].
Для показательной и логарифмической функций, предусмотрена проверка вводимых в текстовое поле данных, с учетом того, что основание больше нуля и не равно 1. Если введены не корректные данные, то на форму выводится текст «Введите значение, а>0» и кнопка «Функция» будет не активна, до тех пор, пока не ввести верные значения.
Свойства функций перечисляются по пунктам из Таблицы 1.
Таблица 1
Пункты свойств функций
|
Обозначение |
Название пункта |
|
«D(f)" |
Область определения |
|
«E(f)" |
Множество значений |
|
«y(-x)= y(x)" |
Четность |
|
«y(-x)= -y(x)" |
Нечетность |
|
"^ OX, y=0" |
Пересечение с осью ОХ |
|
"^ OY, x=0" |
Пересечение с осью ОУ |
|
y(T)=y(x+T) |
Периодичность |
|
«y>0" |
Промежутки, на которых функция положительна |
|
«y<0" |
Промежутки, на которых функция отрицательна |
|
«y " |
Возрастание функции |
|
«y " |
Убывание функции |
|
«Y max» |
Наибольшее значение функции |
|
«Y min» |
Наименьшее значение функции |
|
«Asimptota» |
Асимптоты |
Для закрепления свойства монотонности функций, в программе предусмотрены задания на сравнение выражений. Выбор знака сравнения осуществляется с помощью элемента ComboBox. После, нужно щелкнуть по кнопке «Проверить» и отобразится информация о правильности выполнения задания.
Описанный в статье проект способствует повышению интереса к математике, реализует интерактивность информационного взаимодействия между преподавателем и обучающимися, визуализацию учебного материала, автоматизацию поиска информации и контроль уровня знаний и умений.
Программное приложение «Элементарные математические функции» может быть использовано:
— преподавателями математики и обучающимися при изучении, закреплении, обобщении: понятия функции, виды, свойства и графики, применении функций, взаимно-обратные функции, при решении различных уравнений, неравенств на основе свойств функций.
— преподавателями информатики, алгоритмизации и программирования для демонстрации возможностей компьютера, знакомства с элементами системы программирования VisualBasic, алгоритмическими конструкциями, подпрограммами.
Литература:
- Берман Н. Д. Использование графики в Visual Basic: методические указания и задания к выполнению лабораторной работы по информатике / Н. Д. Берман. — Хабаровск: Изд-во Тихоокеан. гос. ун-та, 2013. — 24 c.
- Гриншпон, И. Э. Элементарные функции и их графики: учеб. пособие / И. Э. Гриншпон, Я. С. Гриншпон. — Томск: Изд-во Томск. гос. ун-та систем упр. и радиоэлектроники, 2017. — 98 c.
- Зуфарова А. С. Программирование в VisualBasic: учебное пособие / А. С. Зуфарова. — Хабаровск: Издательство ТОГУ, 2014. — 84 c.
- Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10–11 классы: учеб. для общеобразоват. организаций: базовый и углубленный. уровни / Ш. А. Алимов и др.-М.: Просвещение, 2021. — 463 с.
- Вербицкая Е. В. Математические функции в жизни / Е. В. Вербицкая // Инфоурок: [сайт]. — URL: https://infourok.ru/matematicheskie-funkcii-v-zhizni-1534920.html
- Перельман Я. И. Занимательная алгебра/Я. И. Перельман. — М. Олма Медиа Групп, 2013. — 125 с.
- Саблина С. А. Применение математических функций в жизни человека и в математике / С. А. Саблина // Инфоурок: [сайт]. — URL: https://infourok.ru/primenenie-matematicheskih-funkciy-v-zhizni-cheloveka-i-v-matematike-2240586.html







