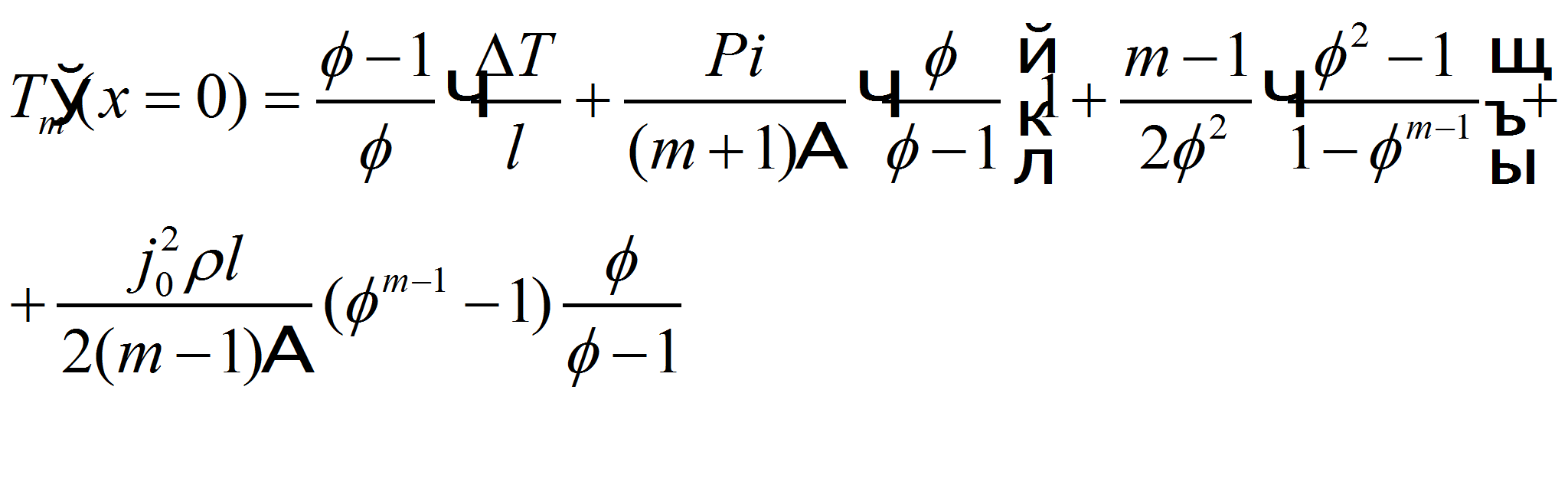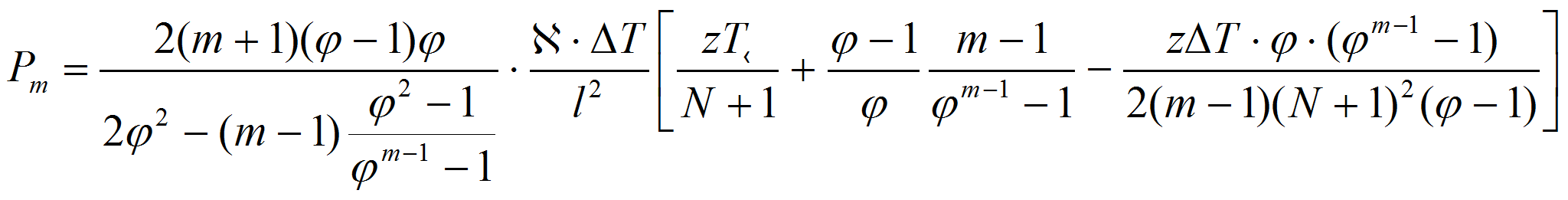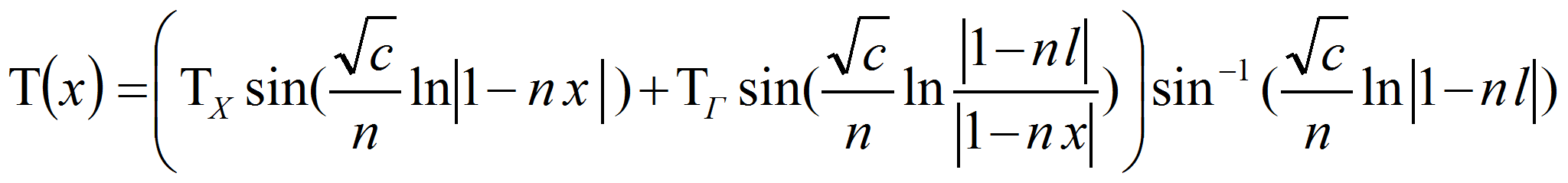Теория эффекта формы полупроводниковых термоэлементов

В ряде работ (см., например, библиографию [1]) для конкретных слу­чаев, теоретически рассмотрен эффект формы термоэлементов с внутренним тепловыделением (ТЭВТ), где в объеме происходит непрерывное тепловыде­ление. В качестве ТЭВТ может служить радиоизотоп [2] и статическая смесь измельченных компонентов термоэлектрических и тепловыделяющих веществ [3]. Ниже не будем останавливаться о преимуществах ТЭВТ по сравнению с обычными термоэлементами, поскольку этот вопрос более подробно ос­ве­щен в [1], и в дальнейшем задачу об эффекте формы в ТЭВТ длиной и площадью поперечного сечения S(x) решим в общем виде

, (1)

где , , , и - радиусы ТЭВТ на горячем и холодном спаях соответственно, - произвольная постоянная ().

Урав­­нение теплопроводности в одномерном случае напишем в виде [4]

, (2)

Здесь - температура , - удельная мощность тепловыделения , - коэф­фициент теплопроводности, - удельное сопротивление образца ТЭВТ, - амплитудное значение плотности тока. Решение уравнения (2), ко­торое описывает распределение температуры по направлению изменения по­перечного сечения ТЭВТ и зависит от постоянной , представим в виде

, (3)
где и - постоянные интегрирования, определяемые из граничных ус­ло­­вий ; . Теперь определим выражение для гради­ен­та температуры в горячем спае

, (5)

откуда, для , сразу получаем формулу (5) [5] Для определения вы­ражения для удельной мощности тепловыделения запишем уравнение теп­лового баланса на горячем спае в виде [5]

, (6)

где , , - сопротивление нагрузки, - внутреннее сопро­тивление ТЭВТ, и с учетом последних двух соотношений имеем:

. (7)

Здесь - нагрузочный коэффициент, - термоэлектрическая добротность, - коэффициент термоЭДС. Тогда коэффициент полезного дей­с­твия (КПД) ТЭВТ определим по формуле

, (8)

где - мощность ТЭВТ: , - объем: 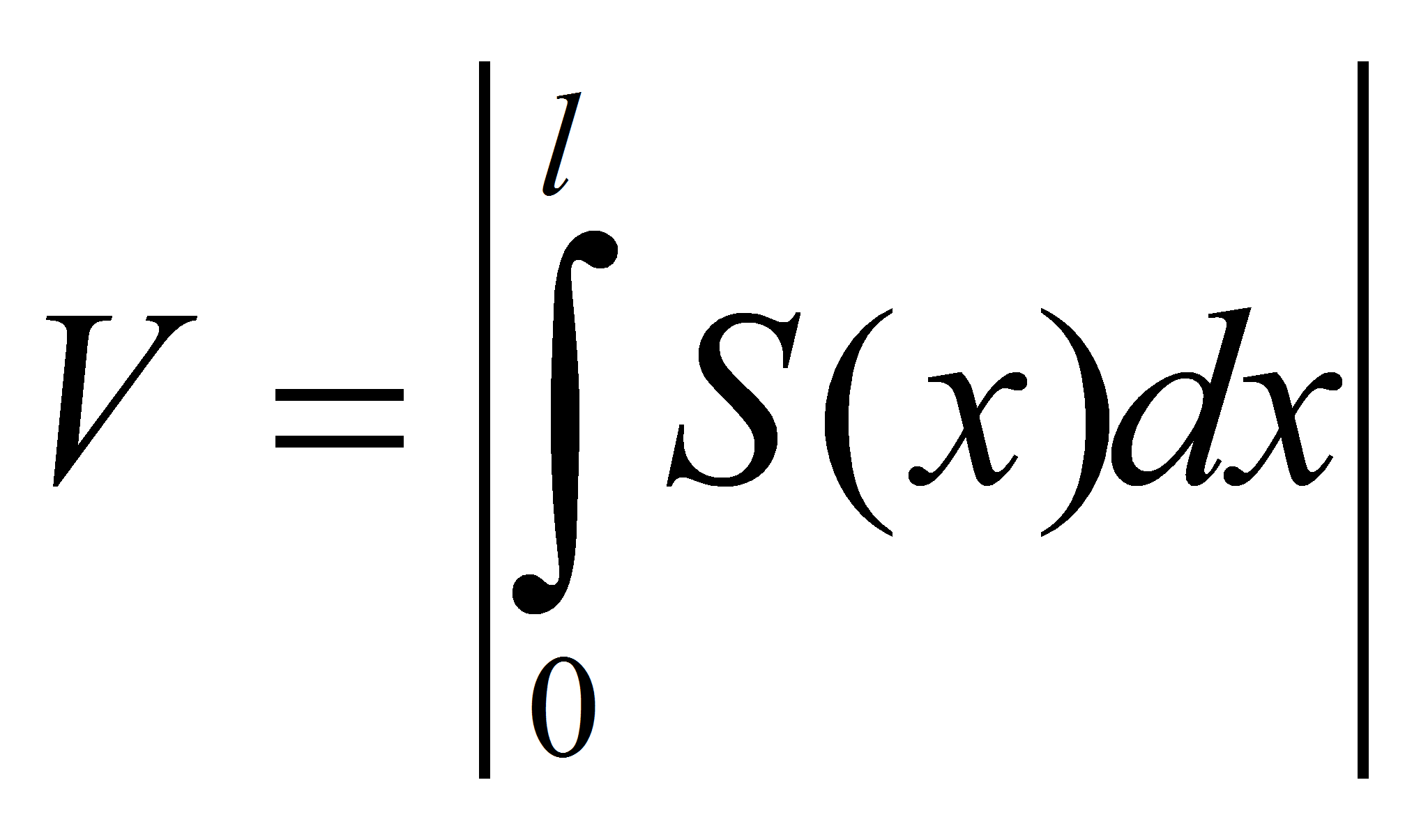. Подставляя (7) в (8) с учетом (1) нетрудно получить функцио­наль­ную зависимость для ТЭВТ с известными пара­мет­рами.

Отметим, что полученные результаты для m=1 непосредствен­но не при­менимы. Поэтому этот случай рассмотрен отдельно в приближение [6]. Не прибегая к конкретным расчетам приведем решение (2) для m=1 :

, (9)

где , - константа, определяемая механизмом электрон – фо­нон­­ного взаимодействия [7]. Ниже приведены численные результаты, рас­считанные по Serpik Graphs для различных значений . Эти расчеты пока­зывают, что при определенных значений возникает нестабильность прос­транственного распре­де­ления температур. Численные значения Т(х) для величин: Т_Х/Т_Г =0,5 и nl=0,5 приведены на таблице 1. Отметим, что в пространственном распре­де­ле­ние Т(х) нулевое значение этой функции встречается при х=0,96 при = 0,1 (экстре­мумы фукции : Т_max =0.79T_Г при х= 0.5 и Т_min = 0.99 T_Г при х=-0.5); а при = 0,01 – встречается при х= 0.47; 0.72; 0.85; 0.92; 0.96; 0.98; 0.99. При тех же значениях величин экстремальные значения Т(х): T_max= 0.27 T_Г при х= 0.5; T_min = 0.61 T_Г при х= -0.5; T_max = 0.79 T_Г при х=0.5; T_min= 0.89 T_Г при х=-0.5; T_max = 0.94 T_Г при х= 0.5; T_min= 0.97 T_Г при х=-0.5; T_max= 0.98 T_Г при х=0.5; T_min= 0.99 T_Г при х= -0.5. Как указано в [147], КПД классического термоэлемента опи­сы­вается формулой

, (9)

Таблица 1

Численные значения Т(х) (при значениях величин: Т_Х/Т_Г =0,5 и nl=0,5)

где для термоэлемента постоянного сечения , (10a)

а для конического термоэлемента [A22] . (10b).

Таким образом установили, что коэффициент полезного действия тер­мо­эле­мен­та зависит не только от температуры термоэлемента, но и от разн­ости темпе­ра­тур горячего и холодного спаев, от геометрических размеров по­пе­реч­ного сечения ТЭВТ и от сопротивлений внешних и внутренних нагрузок.

Литература:

1. Иорданишвили Е.К., Бабин В.П.. Нестационарные процессы в термоэлектрических и термомагнитных системах преобразования энергии. М.: 1983. 216 с.2,

2. Охотин А.С., Ефремов А.А., Охотин В.С., Пушкарский А.С.. Термоэлектрические генераторы. М.: Атомиздат.1976.

3. Патенты США. Кл. 62-3. № 3256696-3256702 , РЖЭЭ. 8А88-8А94П. 1967.

4. Михеев М.А., Михеева И.Н.. Основы теплопередачи. М.: Энергия. 1977.

5. Бабин В.П., Иорданишвили Е.К. // ФТП. 1981. Т.15.В.6.С.1218-1220.

6. Набиева М.Б., Олимов Х., Р.Я., Кодиров А. //ИФЖ. 1998. Т.71. В.3. С.542

7. Ансельм А.И. Введение в теорию полупроводников. М.: Наука. 1978.-616 с.