Разбивка осей сооружений способом линейной засечки



В данной статье рассматривается один из способов разбивки осей зданий и сооружений — способ линейной засечки. Также приведены теоретические основы по определению точности и погрешности способа линейной засечки.

Ключевые слова: разбивка, засечка, погрешность.

Для вынесения в натуру осей сооружений применяется ряд способов разбивки, в том числе линейной засечки (рис.1).

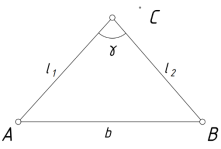
Рис. 1. Схема линейной засечки

В этом способе положение точки С определяется пересечением проектных отрезков и , отложенных от исходных пунктов А и В. Способ линейной засечки простой по выполнению и обеспечивает необходимую точность разбивки на ровной площадке и вблизи пунктов исходной геодезической сети. Отложение отрезков выполняют металлической рулеткой с соблюдением необходимых мер обеспечения точности (компарирования рулетки, натяжения, уложения в створ, многократности построения).

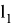
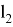
Разбивку осей объекта выполняют в два этапа:

 выносят, от пунктов П1 и П2 исходной основы, точку пересечения осей А (рис.2) отложением проектных (разбивочных) отрезков и (также точку В);

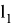
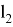
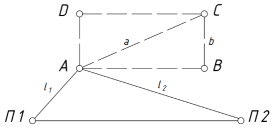
Рис. 2. Разбивка осей сооружения

 от точек А и В, отложением длин отрезков a и b (длины диагонали а и оси b) разбивают точку С, а затем — D. Для контроля измеряют длины линий АВ и CD.

Точность способа линейной засечки определяется рядом погрешностей:

– собственно засечки (геометрия фигуры и точность отложения отрезков и ;

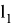
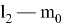
– исходных данных, погрешность положения пунктов П1 и П2, А и В — ;

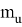
– закрепление точки — .

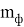
Определяем степень влияния собственно засечки на положение точки С

, (1)

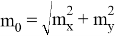
где и — средние квадратические погрешности СКП определения координат точки С.

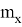
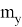
В соответствии с теорией погрешностей запишем

; (2)

. (3)

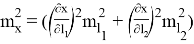
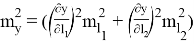
Вычислив частные производные в скобках — формулы (2) и (3), и выполнив некоторые преобразования, запишем

, (4)

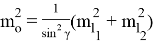
где — угол при вершине С, и — СКП отложения отрезков

и от исходной основы.

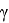
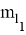
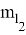
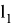
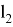
Принимая точность построения отрезков и равными, = = , получим

. (5)

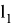
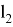
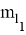
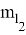
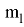
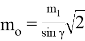
Погрешности в положении пунктов П1 и П2 геодезической сети приведут к смещению точки С (применительно к рис. 2, точке А) относительно проектного положения. Средняя квадратическая погрешность исходных данных вычисляется по формуле

. (6)

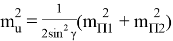
Принимая, = = , получим

. (7)

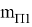
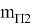
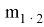
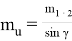
Погрешности фиксации точки зависит от способа закрепления (нанесения) точки, при кернении на металле она составляет 0,5 мм.

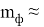
Таким образом, СКП положения точки А на местности можно вычислить по формуле

. (8)

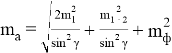
Применяя формулу (8) можно установить:

– минимальный и максимальный угол засечки;

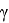
– длины проектных (разбивочных) отрезков и ;

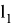
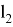
– СКП отложения линий.

Инструктивными материалами определены СКП погрешности разбивки точки оси, они не должны превышать значений:

– в районах многоэтажной застройки — 25 мм;

– в районах малоэтажной застройки — 40 мм;

– на незастроенной территории — 50 мм.

Следовательно, погрешность 0,5 мм, можно считать малой величиной и её можно не учитывать.

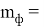
В этом случае формула (8), в общем виде запишется

. (9)

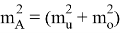
Значение зависит от точности исходной основы, погрешности положения пунктов П1 и П2, обычно полигонометрии 1 или 2 разряда, с относительной погрешностью хода и взаимного положения — 1:20000 и 1:10000 соответственно, а такие длины стороны, в данном случае (рис.2) b.

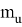
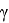
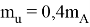
Рассмотрим определение угла на примере — исходная сеть (полигонометрия 1 разряда), длина исходной стороны 200 м. На основе формулы (7) и (9), получим

(10)

и

. (11)

Для случая многоэтажной застройки 25 мм, и 10 мм, угол 0,6. Из этого следует, что угол засечки должен быть не менее 54° и не более 126°.

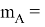
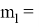
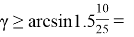
Для вычисления длины разбивочного отрезка формулу (10) запишем в виде

, (12)

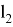
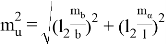
где — первый член формулы выражает влияние погрешности исходной стороны хода; а второй — погрешность определения дирекционного угла этой стороны .

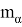
Исходя из формул (10) и (12), запишем

, (13)

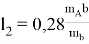
Для тех же условий, что и при выполнении , получим 142 м.

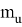
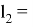
Формула (13) дает возможность устанавливать длины линий в зависимости от территории разбивки и точности обоснования в каждом конкретном случае.

Составив разбивочный чертеж, и по значениям , и можно определить СКП отложения линии по формуле

, (14)

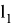
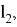
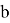
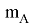
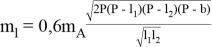
где — полупериметр разбивочного треугольника.

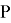
По значению можно разработать методику линейных измерений, обеспечивающую необходимую точность построения разбивочных элементов.

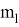
Литература:

1. Авакян В. В. Прикладная геодезия. Технологии инженерно-геодезических работ. 3-е изд. перераб. и доп. — Инфро — инженерия, 2019. — 590 с.