Quantum «Fool» game



The fool is a card game popular on post-USSR area. In classic game the goal of a player is run out cards totally by beating the cards of opponent. We offer a quantum variant of this game to show how quantum mechanics works. The analogies with tunneling effect, Schroedinger function, Heisenberg principle, phase space are founded.

Keywords: quantum mechanics, particle, card rank, classical game, forbidden state, analogue of quantum mechanics.

The modeling of quantum analogies of table games is a useful process. It can describe the quantum processes in system of particles with example from macroworld. The quantum analogies of tic-tac toe have been offered already some years ago [1]. In this article we suggest a type of card game «fool» based on quantum mechanics principles.

The rules of classical fool are simple. The quantity of players is from two to five people. The quantity of cards in deck is usually 36 from 6 to ace. The gradation of rank in card deck is 6 7 8 9 10 J Q K A. Every card can be beaten by trump card of any rank. But trump card can not beat a trump card of higher rank. The player who has a card of least rank starts a game. The attacker put any card face up and defender has to beat this card by trump card or any card of higher rank.

Example 1: The attacker put a 8♥ and trump cards The defender can choose any card ♥ from 9 and higher or use trump. If he is not able to beat he has to take an attacker’s card. The game continues until then only one player has cards in hands.

The rules of quantum game

The every card in a game is a particle in four-dimension Hilbert area of four (♠, ♥, ♣, ♦)

The nominal of every card can be determined as a energy level connected with a pulse. The every card is given with a normalized vector . For example, for any card of ♥ is

, for this card of ♠ is , for ♣ is , for ♦ is . These are clear states and in the classical fool the clear states are met only.

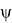
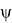
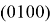
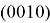
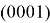
The difference between quantum and classical fool is in nature of states. The quantum state is not determined and can be mixed. For example, the vector means that card «ten» (2+1+3+4) consists of two ♥, one ♠, three ♣ and four ♦.

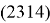
The cards of high ranks are the aces, kings, queens, jacks. These types of cards are considered to exist in a quantum hole with infinite walls. These additional rules mean that card can consist out of one or two suits.

In classical fool we use four queens. The «average» queen is fourth spade, fourth heart and etc.

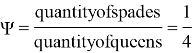
The choice in quantum fool is much bigger. We have 10 queens now(!) Four states are clear and six states are mixed (for example, spade-heart queen pic.1).

The «average» queen, king, jack and ace in quantum and classical fool are similar.

It is possible to calculate all combinations for quantum fool. The number of cards of highest rank are 16 and number of highest cards in quantum fool are 40! (pic.2)

There are 4 cards of every rank in a classical deck. The number of «non-clear» states is different for every card and depends of rank. The russian deck of «fool» consists out of 36 cards but it is allowed to play fool using 52 cards (with or without jokers). The classical card «two» has 4 variants. The quantum card «two» has 10 variants. The quantum «three» has 20 variations (Table 1). The sum of elements in every vector is a rank of card.

Fig. 1. Spade-heart queen

2

Table 1

3♠	3♥	3♣	3♦
(3 0 0 0)	(0 3 0 0)	(0 0 3 0)	(0 0 0 3)

Classical fool: «three»

3♠	3♥	3♣	3♦
(3 0 0 0)	(0 3 0 0)	(0 0 3 0)	(0 0 0 3)
2♠+1♥	2♥+1♠	2♣+1♠	2♦+1♠
(2 1 0 0)	(1 2 0 0)	(1 0 2 0)	(1 0 0 2)
2♠+1♣	2♥+1♣	2♣+1♥	2♦+1♣
(2 0 1 0)	(0 2 1 0)	(0 1 2 0)	(0 0 1 2)
2♠+1♦	2♥+1♦	2♣+1♦	2♦+1♥
(2 0 0 1)	(0 2 0 1)	(0 0 2 1)	(1 0 0 2)
1♠+1♥+1♣	1♥+1♦+1♣	1♥+1♠+1♦	1♠+1♣+1♦
(1 1 1 0)	(0 1 1 1)	(1 1 0 1)	(1 0 1 1)

To make calculations more simple we offer to consider a modified deck with cards

2 3 4 5 6 J Q K A . The probability to win does not depend on consistence of a deck. Decks 6 7 8 9 10 J Q K A and 2 3 4 5 6 J Q K A are similar.

Table 2

The other variant of fool with forbidden state «1»

Rank	Number of cards in a classical deck	Number of cards in a quantum deck
2	4	10
3	4	20
4	4	34
5	4	52
6	4	80
Jack	4	10
Queen	4	10
King	4	10
Ace	4	10
Total number of cards in deck:	36	236

The difference between classical deck and quantum deck is shown in Table 2

The formula for receiving quantity cards of every rank in quantum fool is:

(1)

is an amount of ways to create a natural number as a sum of natural numbers.

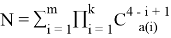
For example: 3= 3, 2+1, 1+1+1. (3)=3.

is an amount of groups of subtrahends. For 2+1 is 2 (2+1, 1+2), for 1+1+1 is 1

is a quantity of similar subtrahends. For 1+1+1 is 3.

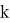
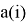
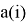
The number «1» in every term could be analog of forbidden state, because rank «one» does not exist in deck. The deck 6 7 8 9 10 J Q K A with least element 2 of vector is shown in Table 3. The rank 6 is presented in this case by three ways only:

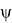
6=4+2( =2)=3+3( =1)=2+2+2( =1) ( =3). The players may use any variants of game with «1» or without «1». The choice of game is not a problem of quantum mechanics and we end this part of article. (Table 3)

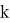
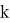
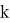
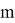
Table 3

The other variant of fool with forbidden state «1»

Rank	Number of cards in a classical deck, N	Number of cards in a quantum deck, N
6	4	26
7	4	40
8	4	47
9	4	72
10	4	100
Jack	4	10
Queen	4	10
King	4	10
Ace	4	10
Total number of cards in deck, Q:	36	325

The game

A rank of card could be named analog of energy level of particle. The quantum mechanics is known to exist a commutation of operators.

(2)

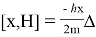
The coordinate and Hamiltonian are not determined at the same time. The suit and rank are not determined at the same time in quantum fool because the player knows only rank of card but suit could be mixed. The absence of determined suit is analogue of electron cloud in atom. Given the fact the atom is a quantum well, numerized energy levels (ranks), we suppose a card to be in any potential field in a quantum well.

A card is an analogue of particle and it owns a wave function for every rank.

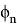
This function is defined as: { (3)

{

are amounts of signs of spades, hearts, diamonds and clubs in card of every rank, is a rank, is total amounts of cards in deck,

is quantity of cards given rank(clear states with one suit only are included too). are orthogonal functions because of equality to zero in some volume of four-dimension suit area. Example: For card «7» (deck from Table 3) The particle inside of quantum well with infinite walls owns a zero wave function outside this well. The authors suggest to imagine every card in quantum fool to be in well with these walls because of zero wave function presence.

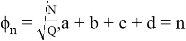
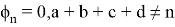
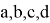
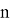
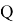
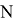
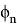
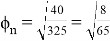
The quantum laws manifest them in beating of card. The particle with small energy is able to penetrate through high energy barrier. It is known as a tunneling effect. In quantum fool a player can beat a card of higher rank by one or more card of little rank. For example, an attacker put a card 7 (2♦+2♥+3♠). The defender can beat 2♦ it by 5♦, 2♥ by 6(3♥+3♠) and 3♠ by card 6 (for example, 4♠+2♣ or every other card 6 and higher).

Also authors suggest to watch other situation: an attacker put 8 (5♠+3♥), the defender beat it with jack(♠+♥). Roughly speaking, the participants are playing at the same time two games. In first universe jack of spades beats a five of spades. In second universe jack of hearts beats three of hearts. (pic.2).

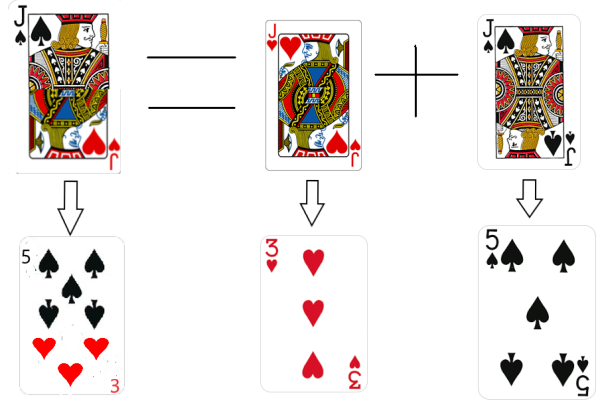
Fig. 2. The example of card superposition

Is Heisenberg uncertainty principle correct for situation with cards? The principle is right in this case but not completely. In classical fool player looking at number of card and one sign from its face can compute the suit of card. In quantum fool the observer had to look at card completely to solve the proportion of every suit in card. The average proportion of every suit in card of every rank is equal to 0.25 as in classical fool.

Looking at situation jack(♠+♥) against 5♠+3♥ we made some interesting conclusions. When defender beats a 5♠ by jack of spades, this pair of cards «annihilates» and system of cards changes the position in suit area turning into (3♥, jack of hearts) only. The game can go on. In this game we do not consider a changing of suit signs on card.

Conclusions

The quantum laws were applied in situation with card set. The difference between classical and quantum fool lies in suits. In quantum card game it is possible to be a few suits on one card simultaneously. There were described analogues of tunneling effect (beating by one card other card of higher rank), wave functions, determined as square roots from probability finding the rank in a deck. The suits create four dimension space, analogue of coordinate space but it is able to model a game version with suits as quantum numbers (spades are equivalent of magnetic quantum number and etc.). The rules for game were not developed completely. However it was not a purpose of this article. Authors wanted to tell about quantum mechanics principles with help of usual stuff. This article could be useful for teaching and it may be useful in entertainment.

References:

1. Goff. Quantum tic-tac toe: A teaching metaphore for superposition in quantum mechanics.: Am. J. Phys. 74, 962 (2006)