1. Введение
В предыдущей работе [1] были описаны действие на основе суммы цифр разрядов (далее СЦР) и свойства, связанные с ней. Однако есть одна неточность, которая не была упомянута. Там, где указана принадлежность к отрезку [0;9], требуется дополнительное уточнение: данный отрезок принадлежит множеству целых чисел.
В данной работе действие СЦР будет рассмотрено как функция, а также будут рассмотрены уравнения, связанные с СЦР, и способы их решения. Далее они будут обозначаться как кси-уравнения и кси-функции.
2. Кси-уравнения
В предыдущей работе было описано действие СЦР. Для удобства разбора кси-уравнения будут рассматриваться на основе КСЦР, так как КСЦР имеет удобную форму. Также введем множество цифр, далее обозначим его как:
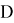
2.1
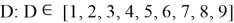
Уравнение будем называть кси-уравнением, если оно будет иметь следующий вид:
2.2
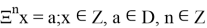
Так как рассматривается КСЦР, то решать можно в общем виде. Распишем общий вид КСЦР:
2.3

Где
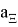
Для решения уравнения 2.2 можно воспользоваться формулой 2.3, однако поменять начальные условия 2.2:
2.4
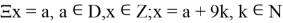
Уравнение 2.4 будем называть каноническим кси-уравнением. А его решение каноническим решением.
Рассмотрим другой вариант уравнения 2.3:
2.5
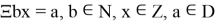
Чтобы решить данное уравнение, воспользуемся каноническим решением 2.4. Тогда решение уравнения будет выглядеть:
2.6
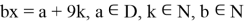
Так как решение требуется в целых числах, то просто поделить на b нельзя, но можно вывести общее решение. Из 9k вычтем столько порядков t, чтобы выражение
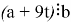
2.7
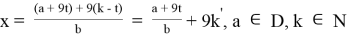
У этого уравнения есть следующие ограничения:
b
≠3
n
и
a
≠3
k
, так как в таком случае уравнение или не имеет решений, или a= 3
k’
. Так как период КСЦР равен 9, то и все числа, кратные 9, имеют КСЦР равный 9. С числами вида 3k(3n), КСЦР будет менять свое значение на
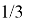
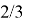
Как и с любым видом уравнений, из кси-уравнений можно составлять другие уравнения или системы уравнений. Примеры таких уравнений:
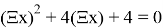
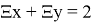
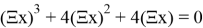
Представленные уравнения легко решаются методом замены: Ξ x = t. Как только находятся значения замены, уравнение решается как каноническое.
3. Кси-функции
На основе кси-уравнений можно составить функции и исследовать их. В качестве примера возьмем функцию на основе канонической формы 2.4 на множестве целых чисел:
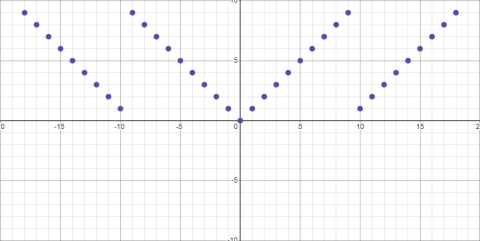
Как видно из графика выше, функция принимает нулевое значение только в точке ноль, дальше каждое значение 1+9 k функция принимает локальный минимум, на каждом 9 k — максимум.
Все переменные, которые будут указываться далее, относятся к натуральным числам.
Стоит отметить, что во множестве натуральных чисел функция неразрывна. На множестве действительных чисел картина не изменится, а для расширения на действительные числа требуется вводить ПСЦР.
Отдельно стоит рассмотреть функцию, которая будет ссылаться на формулу 2.5. Рассмотрим функция с параметром b =2:
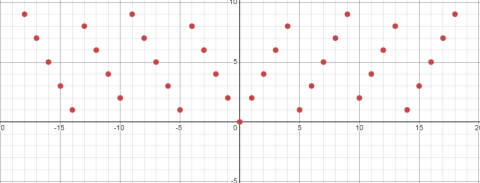
Как видно из графика, точки сместились, и функция стала уже. Однако максимумы и минимумы не изменились, они теперь повторяются каждые 18 k раз.
Отдельного внимания стоит функция с параметрами b, равными 3,6 и 9:
b =3
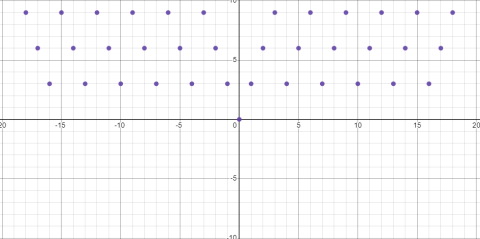
b =6
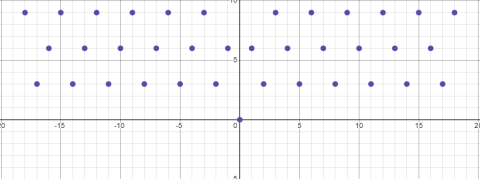
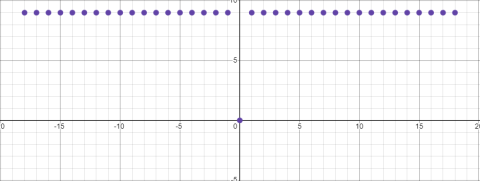
b =9
Для случаев, когда b равно 3 и 6, минимумы смещаются на значение 3 и чередуются каждые 3 k и 6 k значений соответственно.
Для случая b =9, функция превращается в прямую y =9, исключая точку 0. В точке 0 функция принимает значение 0 для любого значения b .
Также из кси-функции можно создавать составные функции:
3.1

Ниже представлен график функции 3.1 при условии
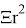
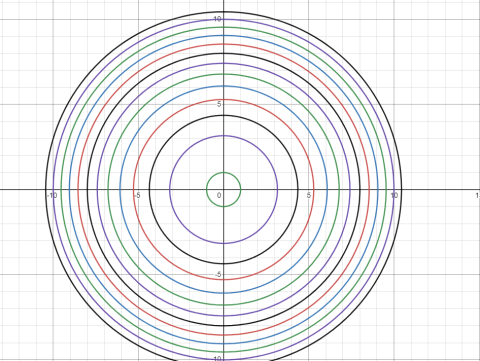
График представляет собой множество окружностей, квадрат радиуса которых является решением уравнения
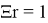
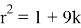
Рассмотрим другую похожую функцию:
3.2

Зададим условие
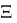
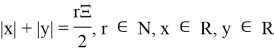
Таким образом, больше линий поместится на экран:
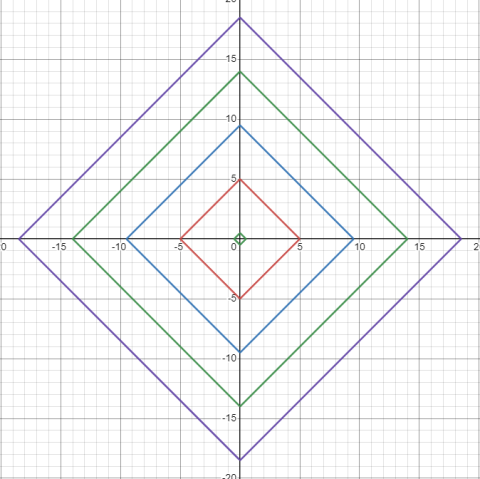
4. Вывод
Эта работа графически представила действие КСЦР. Введены определения функций и уравнения на основе КСЦР и СЦР — кси-функции и кси-уравнения. Выведены и показаны основные виды функций и уравнений. Это позволит разбирать эти определения с помощью элементов математического анализа.
Литература:
- Шаповал, А. Н. Сумма цифр разрядов и её свойства / А. Н. Шаповал. — Текст: непосредственный // Молодой ученый. — 2023. — № 29 (476). — С. 1–5
- Графики функции построены на свободном ресурсе в интернете — desmos.com







