Предлагаемая нами методика изучения явления интерференции строится на основе метода, который может являться общим для исследования полей физических величин, — метода компьютерной визуализации. Использование метода компьютерной визуализации при обучении физике опирается на общедидактические принципы научности, системности, доступности и наглядности. Кроме этого, можно сформулировать частнодидактические принципы применения метода компьютерной визуализации полей физических величин при обучении физике. Они могут быть следующими.
Принцип освоения и использования учителем. Формирование понятия поля физической величины будет полным, если при изучении полей учитель будет систематически применять метод компьютерной визуализации, как универсальный метод исследования полей физических величин.
Принцип изучения и использования учащимися. Метод визуализации относится к общефизическим методам исследования, поэтому обучаемые должны не только понимать его сущность, но и реально уметь его применять в своих исследованиях.
Принцип компьютерного сканирования. Количественное сканирование целесообразно реализовать в полуавтоматическом варианте, когда обучаемым демонстрируют значение физической величины в различных областях пространства исследуемого поля. При этом картина поля должна быть максимально проста и доступна для понимания. В случае необходимости осуществляется снижение размерности картины пространственного распределения физической величины.
Сканированием мы называем метод поточечного исследования поля физической величины, в результате которого получается визуализированное изображение определенной области поля или графическое изображение зависимости физической величины от координат точек этой области.
Принцип доступности и надежности программного обеспечения. Программа для компьютерной визуализации должна отличаться простотой в обращении, надежностью полученных результатов и быть доступной обучаемым для понимания.
Дидактические материалы технических средств обучения должны соответствовать определенным требованиям [1, с. 159]. Компьютерные визуализирующие программы должны:
иметь конкретное дидактическое назначение;
соответствовать определенному этапу обучения;
соответствовать научному уровню учебного материала и его логическому построению;
учитывать преемственность знаний и опираться на ранее полученные обучаемыми знания;
обеспечивать научные и методические связи между структурными элементами учебного материала;
создавать условия для решения комплекса образовательных, воспитательных и развивающих задач;
содержать в себе программу управления познавательной деятельностью обучаемых;
учитывать уровень подготовленности обучаемых;
использовать выразительные средства для передачи информации различного вида.
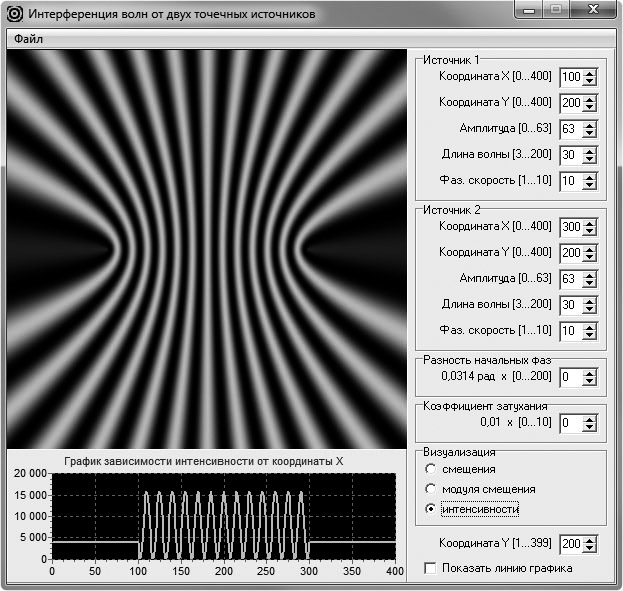
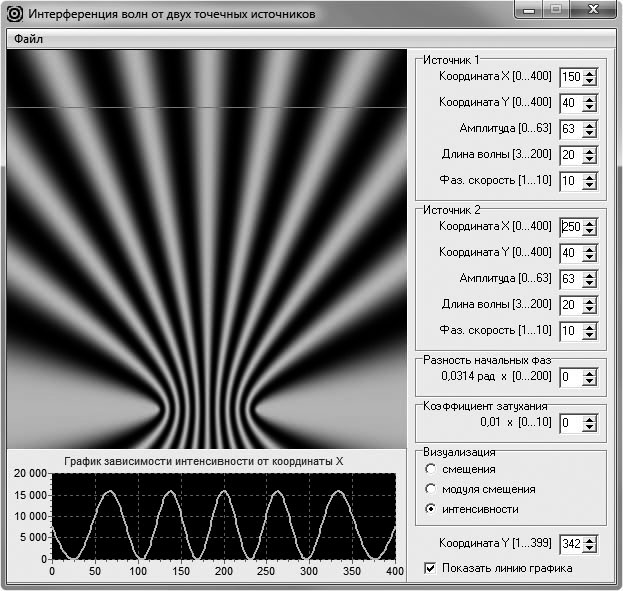
Рассмотрим, каким образом может быть организовано теоретическое изучение явления интерференции волн от двух точечных источников с помощью метода компьютерной визуализации, которое может происходить в сочетании с экспериментальным исследованием, описанным нами в статье [2]. Для этого разработана компьютерная программа, моделирующая картину пространственного распределения смещения, модуля смещения или интенсивности результирующей волны, образующейся при интерференции волн, распространяющихся от двух точечных источников. Программирование графики осуществлялось с применением библиотеки DirectX (модуля DirectXGraphics среды программирования Borland Delphi). Основное окно приложения содержит два вида распределений (двумерное и одномерное), которые находятся в его левой части. В правой части расположены элементы управления условиями виртуального эксперимента. Возможно изменение координат источников волн, значений амплитуд, фазовых скоростей и длин испускаемых ими волн. Кроме того, пользователю программы предоставляется возможность изменения разности начальных фаз волн и коэффициента затухания. Также он может выбрать, какой вид распределения будет выводиться на экран: распределение смещения волны, модуля этого смещения или распределение интенсивности волны. В программе предусмотрен выбор позиции размещения прямой, вдоль которой проводится сканирование двумерного распределения для получения одномерного распределения, являющегося более привычным для обучаемых, так как именно такого вида распределения (линейные графики) они чаще всего могут видеть на страницах учебников.
Известно, что при интерференции двух одинаковых сферических волн поверхностями равных разностей фаз будут являться гиперболоиды вращения с фокусами в точках расположения источников волн. Иными словами, распределения выбранных нами характеристик результирующей волны будут четырехмерными (каждой точке распределения будут соответствовать три пространственные координаты и четвертый параметр — характеристика волны в этой точке). В таком виде визуализация распределений для учебных целей невозможна. В этом случае, как правило, используют такой известный прием, как снижение размерности. Избавимся от одной из пространственных координат. В этом случае мы получим множество трехмерных распределений, каждое из которых соответствует определенному значению третьей, исключенной нами координате. Однако и трехмерная картина распределения является достаточно сложной для восприятия и анализа обучаемыми. Поступим следующим образом. Будем представлять распределение на координатной плоскости, сопоставив значению характеристики интерферируемой волны соответствующий оттенок одного цвета, например, зеленого. Такое распределение можно изобразить на плоскости, и оно будет более понятным для обучаемых.
При демонстрации компьютерной модели следует обратить внимание обучаемых на то, что согласно современным представлениям область пространства, в каждой точке которой существует физическая величина, называют полем физической величины. В общем случае поле является трехмерным, однако можно упростить задачу и рассматривать двумерные и одномерные поля. Таким образом, для формирования понятия волнового поля учителю целесообразно применять демонстрации, которые предоставляют обучаемым возможность установить связь между физической величиной, характеризующей поле в данной точке пространства, и координатами этой точки. Ясно, что такую связь (или зависимость значения физической величины от координат точек пространства) можно визуализировать, используя математическую модель изучаемого физического явления и графические возможности компьютера.
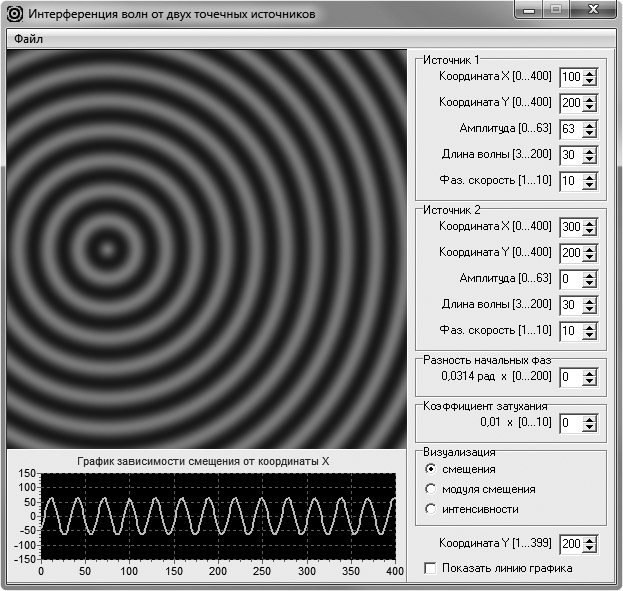
Перейдем к описанию методики изучения интерференции с помощью ее компьютерной модели. Сначала обучаемым демонстрируют поле смещения волны одного из источников (рис. 1). Указывают на то, что данная волна является сферической, так как обучаемые видят двумерное распределение, где линии равных фаз представляют собой окружности с центром в точке расположения источника волны. С помощью одномерного распределения (графика зависимости смещения от пространственной координаты) учащиеся могут легко убедиться, что данная волна является гармонической.
Рис. 1
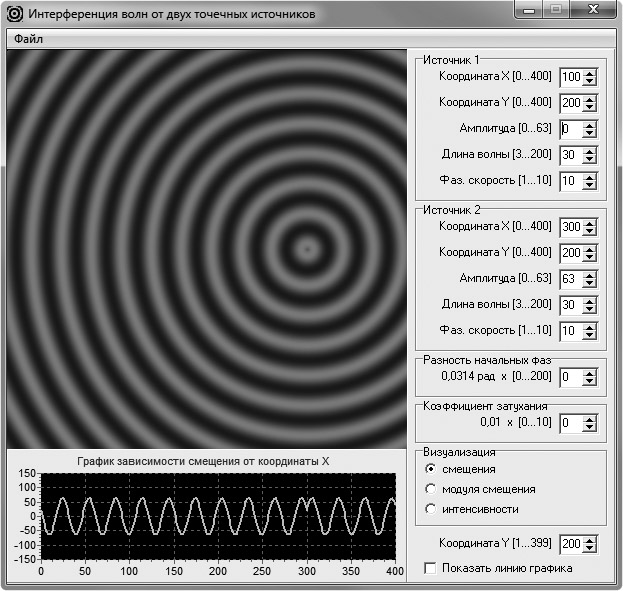
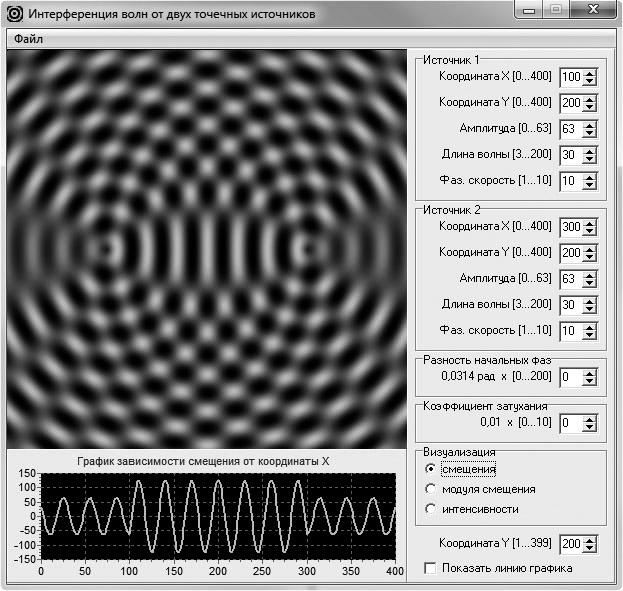
После этого демонстрируется поле смещения уединенной волны, распространяющейся от второго источника (рис. 2). Она обладает такими же характеристиками. Обращают внимание обучаемых на то, что продемонстрированные им волны являются когерентными. Затем учитель может создать проблемную ситуацию, задав вопрос о том, что будет наблюдаться, если обе волны будут распространяться в пространстве одновременно. После запланированной дискуссии демонстрируется результат наложения волн (рис. 3). Обращают внимание обучаемых на то, что между источниками возникла стоячая волна. Наблюдаемые картины распределений позволяют учителю сформировать у обучаемых наглядный образ явления интерференции.
Рис. 2
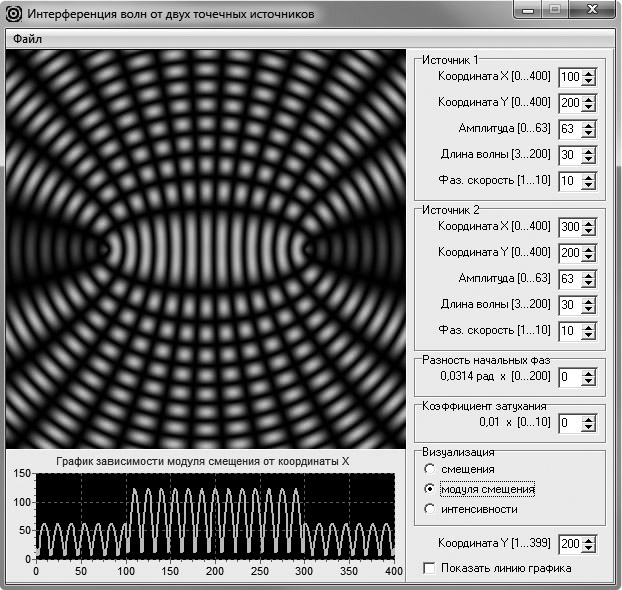
Следующий этап — это визуализация математического поля модуля смещения интерферируемой волны. Демонстрация распределения модуля смещения (рис. 4) необходима из дидактических соображений. При наличии этой демонстрации логический переход от распределения смещения (рис. 3) к распределению интенсивности (рис. 5) при изучении интерференции волн становится более очевидным. Это помогает сформировать понятие интенсивности волны, как некоторой усредненной характеристики, так как обучаемые видят, что в случае демонстрации распределения интенсивности волны картина поля становится статичной. На этом же этапе формируется понятие максимумов и минимумов интерференционной картины.
Рис. 3
Рис. 4
Рис. 5
Рис. 6.
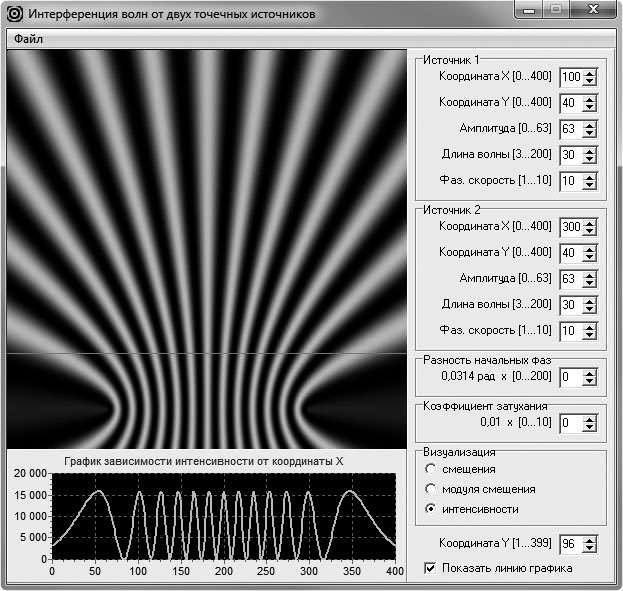
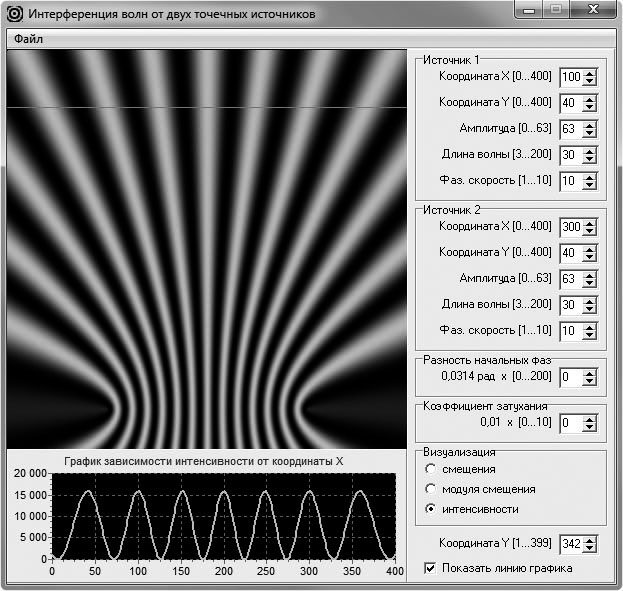
Далее исследуют зависимость интерференционной картины (распределения интенсивности) от условий виртуального эксперимента. Для этого помещают источники волн в нижнюю часть (или верхнюю часть) окна для вывода двумерного распределения и размещают прямую, вдоль которой получается одномерное распределение, недалеко от источников (рис. 6). Указывают на то, что наблюдаемая интерференционная картина отличается от приведенных в учебниках. Это объясняется тем, что картины, изображенные в учебниках, получены аналитическим путем, когда считалось, что расстояние от источников до наблюдаемой интерференционной картины является «очень большим». Предлагают обучаемым запомнить картину распределения, после чего отодвигают прямую сканирования от источников. Замечают изменение картины одномерного распределения, которое заключается в том, что максимумы интерференционной картины стали шире, и расстояния между ними стали больше (рис. 7). При этом картина одномерного распределения стала больше похожа на картины в учебниках, которые были получены аналитически.
Рис. 7
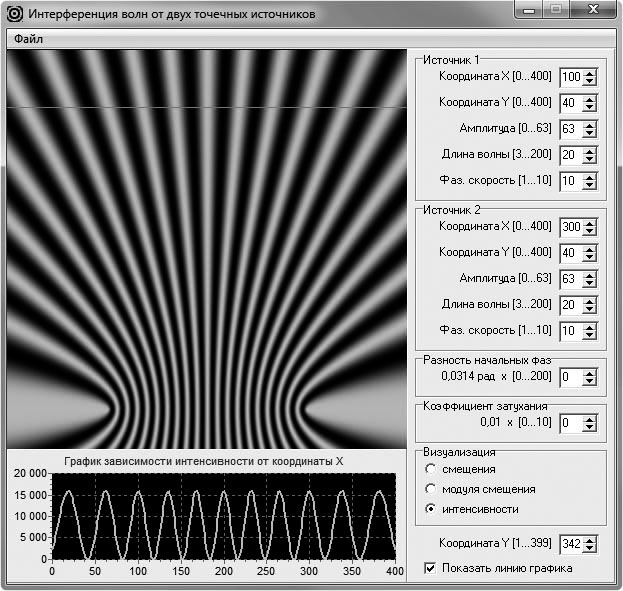
Затем, не меняя расположения прямой, вдоль которой наблюдают одномерное распределение, существенно изменяют длины обеих волн (например, уменьшают их в два раза). При этом наблюдают изменение распределения интенсивности, которое заключается в том, что ширина максимумов и расстояния между ними также уменьшаются в два раза (рис. 8). Многократно синхронно изменяя длины волн, демонстрируют, что увеличение длин волн приводит к расширению максимумов интерференционной картины, а их уменьшение — к сжатию.
Рис. 8
Следующая демонстрация вновь происходит без изменения расположения прямой, вдоль которой получается одномерное распределение интенсивности результирующей волны. Сначала демонстрируются распределения с одним расстоянием между источниками волн (рис. 8), а затем — с другим (рис. 9). Убеждаются, что при уменьшении этого расстояния максимумы картины распределения становятся шире, а расстояния между ними — больше; и наоборот, при увеличении расстояния максимумы сужаются, и расстояния между ними уменьшаются.
Рис. 9
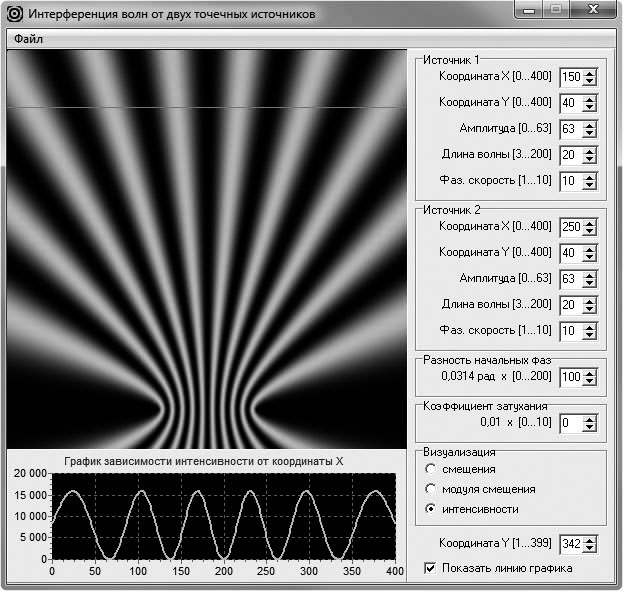
На заключительном этапе демонстрируют зависимость интерференционной картины от разности начальных фаз волн, испускаемых источниками. Сначала показывают картину распределения, когда эта разность равна 0 (рис. 9). Затем получают распределения интенсивности при разности фаз, равной π (рис. 10). При этом наблюдают, что первоначально в центре картины наблюдался максимум, а во втором случае — минимум интенсивности.
В заключении отметим, что эта серия демонстраций может быть использована в школьных условиях, если учитель, владея соответствующей теорией, умеет на доступном обучаемым уровне объяснять все наблюдаемые явления. Действия учителя при демонстрациях заключаются в следующем. Учитель создает исследуемое волновое поле, задавая характеристики волн, и размещает нужным образом прямую, вдоль которой проводится сканирование для получения графика зависимости характеристики волны в точке от координаты этой точки. Вместе с обучаемыми он анализирует полученные картины распределений. Затем учитель изменяет условия виртуального эксперимента, и компьютерное моделирование поля осуществляется заново. Сравниваются полученные результаты, высказываются догадки, строятся предположения, планируется и проводится новое моделирование. Поскольку распределение на экране появляется практически мгновенно, то исследование волнового поля на уроке происходит динамично, и при этом в процессе активно принимают участие обучаемые.
Рис. 10.
Созданная компьютерная программа, соответствующая указанным выше дидактическим принципам, обеспечивает:
проведение моделирования волнового поля в режиме реального времени;
проведение поточечного сканирования поля;
осуществление количественного графического представления результатов;
проведение сравнения результатов различных виртуальных экспериментов.
Опыт использования этой программы при обучении позволяет говорить о том, что метод компьютерной визуализации может быть с успехом использован непосредственно на уроках физики. При этом не только формируется обобщенное понятие волнового поля, но и обеспечивается формирование у обучаемых умений постановки и анализа численного эксперимента с использованием компьютерных технологий. Используя данное приложение, можно осуществить полный познавательный цикл, при котором сначала строится теоретическая модель; из нее выводятся следствия, из которых вытекают условия виртуального эксперимента, и определяется его результат; проводится анализ результата, который укладывается в рамки теоретической модели или противоречит ей. В этом цикле наиболее трудоемкий и времязатратный процесс сбора и обработки данных выполняет компьютер. Учитель и учащиеся в течение относительно небольшого промежутка времени могут исследовать сложное волновое поле. Кроме того, у них появляется возможность сопоставить условия умозрительных задач из учебника с условиями компьютерного моделирования.
Литература:
Коджаспирова Г. М. Технические средства обучения и методика их использования: Учеб. пособие для студ. высш. учеб. заведений / Г. М. Коджаспирова, К. В. Петров. — М.: Издательский центр «Академия», 2003. — 256 с.
Майер В. В. Исследование волновых полей методом компьютерного сканирования / В. В. Майер, О. Е. Данилов // Учебная физика. — 2005. — № 1. — С. 153–186.