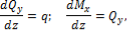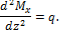Для студентов средних специальных учебных заведений строительных специальностей, как и для других технических, крайне необходимым является усвоение цикла естественно-научных дисциплин, в частности математики.[1]
Общие вопросы необходимости должного уровня математического образования в средних специальных учебных заведениях в литературе были освещены многими авторами, такими как Л. Н. Кашинцева [3], И. Б. Невзорова [4], И. В. Николаева [5], М. И. Башмаков [2], О. А. Арюкова [1] и др. Однако авторами зачастую не приводится конкретики, т. е. не показано на примерах, где и в какой форме необходимы знания математики и умения их применять.
Все авторы сходятся во мнении, что математика для техников необходима, и этому существует множество причин. Но одна из причин является наиболее очевидной: без знания математики решение многих практических задач в рамках специальных дисциплин становится недоступным.
Рассмотрим статический расчет строительных конструкций, получивших очень широкое распространение, — балок. Данный расчет содержится в практических работах в рамках дисциплины ОП.02 «Техническая механика» для специальности 08.02.01 «Строительство и эксплуатация зданий и сооружений». [8]
Для студентов умение производить статический расчет балки практически равно успешно освоенной дисциплине, части это расчета представлены в целых 19 практических работах (Практическая работа № 1 — № 19), из общего количества — 25 работ на всю дисциплину. [7]
Статический расчет сводится к грамотному определению внутренних усилий в балке и построению эпюр поперечных сил и изгибающих моментов, возникающих в результате приложения различного рода нагрузок. На рисунках 1 и 2 приведены случаи плоского и чистого изгибов.
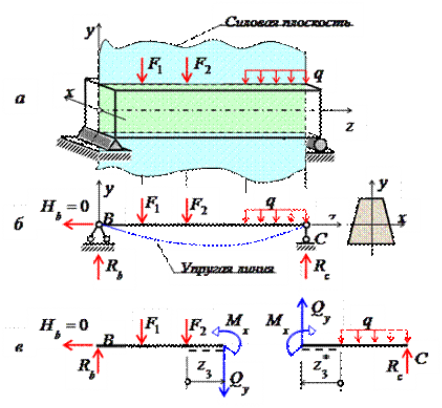
Рис. 1. Плоский или прямой изгиб
При плоском поперечном изгибе в балке возникают два вида внутренних усилий (рисунок 1, в): поперечная сила Q y , где y — ось симметрии (главная центральная ось) и изгибающий момент M x ., где x — другая главная центральная ось сечения, нормальная к оси симметрии.
Если изгибающий момент M x является единственным внутренним силовым фактором, то такой изгиб называется чистым (рисунок 2). При наличии поперечной силы Q y изгиб называется поперечным.

Рис. 2. Чистый изгиб
Непосредственная связь с математикой сразу прослеживается. Приступая к изучению теоретической стороны вопроса, студенты сталкиваются со следующим определением: «Эпюра внутренней силы — график, показывающий изменение этой силы по длине балки». А следом с понятием «Основные дифференциальные соотношения теории изгиба». А далее с фразами: «Правила построения эпюр поперечных сил и изгибающих моментов являются следствием дифференциальных и интегральных зависимостей»[2], «В сечении, где поперечная сила равна нулю, изгибающий момент достигает экстремального значения (максимального или минимального)».
Каждая из вышеперечисленных фраз мысленно отсылает студентов к одному очень важному и довольно сложному для них разделу Дисциплины «Математика» [8] — «Основы дифференциального и интегрального исчисления». [6]
Дифференциальные зависимости при изгибе, существующие в виде теоремы Журавского (теоремы Шведлера)[3] позволяют установить особенности эпюр поперечных сил и изгибающих моментов. Всего таких особенностей около десяти. Некоторые из них:
— В тех сечениях балки, где Q = 0, изгибающий момент экстремален по величине ( М max , M min ).
— Эпюра Q представляет собой диаграмму производной от эпюры M . Значит, ординаты Q пропорциональны тангенсу угла наклона касательной к эпюре M.
— Приращение функции изгибающего момента на рассматриваемом участке численно равно площади эпюры поперечных сил на этом участке с соответствующим знаком.
Статический расчет балки довольно сильно связан с вопросами дифференциального и интегрального исчисления. Поэтому успех освоения технической механики связан с успехом освоения математики курсом ранее.
Преподавателям математики следует уделять особое внимание тем темам и разделам дисциплины, которые особенным образом коррелируют со специальными дисциплинами. Ведь от этого зависит общий уровень подготовки выпускников средних специальных учебных заведений.
Литература:
- Арюкова О. А. Математика в формировании профессиональной компетенции специалиста в учреждениях СПО// International Journal of Humanities and Natural Sciences. — vol.10–1. — С.37–39.
- Башмаков, М. И. Примерная программа учебной дисциплины «Математика для профессий начального профессионального образования и специальностей среднего профессионального образования» [Электронный ресурс]/ М. И. Башмаков, А. Г. Луканкин. М.: ФГУ «ФИРО» Минобрнауки России, 2008. http://www.morb.ru/professional/spo/prog/mat.doc — 24с.
- Кашинцева Л. Н. О проблемах математической подготовки студентов технического колледжа // Национальная ассоциация ученых (НАУ). — 2015. — № VII (12).
- Невзорова И. Б. Особенности подготовки будущих техников-программистов к профессиональной деятельности в процессе обучения математике в контексте компетентностного подхода// Евразийский Союз Ученых (ЕСУ) — 2015. — № 8 (17).
- Николаева И. В., Крылов Д. А. Модель формирования математической компетентности студентов колледжа // Вестник Марийского государственного университета. — 2017. — Т.11. — № 3. — С.33.
- Рабочая программа учебной дисциплины ЕН.01 Математика «Краснодарский колледж управления, техники и технологий» специальность 08.02.01 Строительство и эксплуатация зданий и сооружений.
- Рабочая программа учебной дисциплины ОП. 02 Техническая механика «Краснодарский колледж управления, техники и технологий» специальность 08.02.01 Строительство и эксплуатация зданий и сооружений.
- Учебный план среднего профессионального образования НА 2022–2023 уч. год «Краснодарский колледж управления, техники и технологий» по специальности среднего профессионального образования базовой подготовки 08.02.01 Строительство и эксплуатация зданий и сооружений.
[1] ЕН 01. Математика (в рамках ЕН.00 Математический и общий естественнонаучный цикл)
[2] Дифференциальные зависимости между q, Qz и Мy.
[3]