Формула Маклорена характеристического многочлена для квадратной матрицы размерности 5



В статье получена формула Маклорена характеристического многочлена для квадратной числовой матрицы размерности 5.

Ключевые слова: формула Маклорена, квадратная матрица размерности 5.

Рассмотрим числовую матрицу

Ее характеристическим многочленом называется

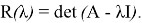
Цель работы: получить формулу Маклорена разложения этого многочлена по степеням .

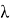
Этот результат может применяться, например, при решении систем дифференциальных уравнений.

Введем функции, построенные с помощью определителя от скалярных функций , :

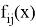
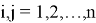
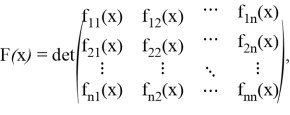
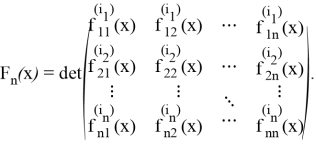
Обозначим полиномиальный коэффициент. Для него справедливо следующее полиномиальное тождество, которое проверяется непосредственно.

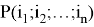
Утверждение 1.

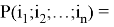
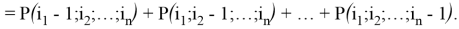
Далее, имеет место следующая формула производной.

Далее, пусть

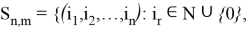
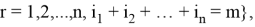
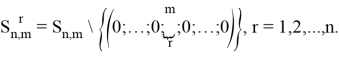
Утверждение 2 .

(1)

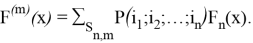
Доказательство. Докажем формулу (1) методом математической индукции по m .

При она верна (см., напр., [1]).

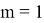
Пусть она справедлива для . Тогда для имеем:

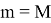
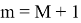
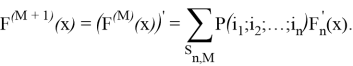
Раскроем скобки; в первой сумме вынесем слагаемое по набору , во второй сумме — слагаемое по набору и так далее, в последней сумме — слагаемое по набору ; сделаем замены: в первой сумме заменив на , во второй сумме на и так далее, в последней на ; применим утверждение 1. Получим:

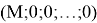
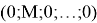
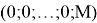
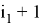
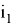
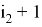
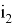
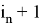
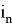
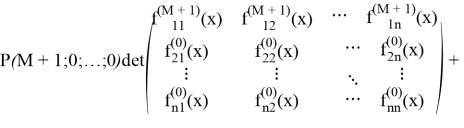
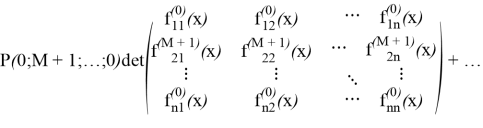
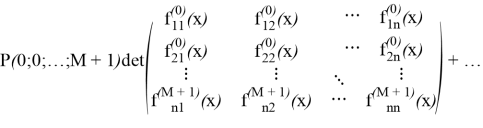
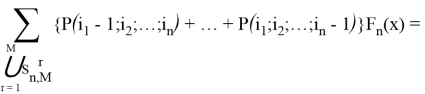
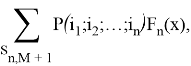
что и требовалось доказать.

Теперь пусть — определитель матрицы, полученной из матрицы A последовательным исключением строки и столбца, затем строки и столбца и так далее до строки и столбца включительно.

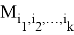
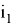
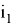
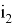
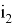
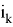
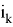
Справедлива следующая формула Маклорена.

Утверждение 2.

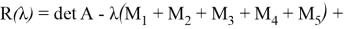
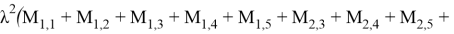
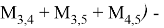
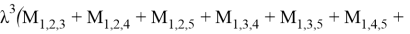
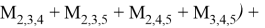
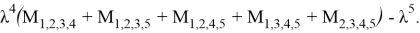
Доказательство. Формула Маклорена для — это (см. [2])

(2)

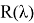
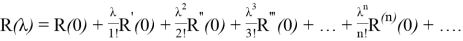
Заметим, что . Далее, в силу утверждения 1 при

,

(3)

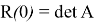
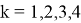
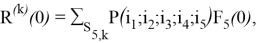
где

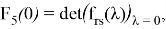
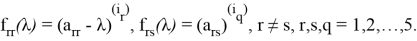
Нетрудно видеть, что , , при . Следовательно, определители по всем наборам, содержащим компоненту больше или равную 2, равны 0, так как содержат целиком нулевую строку. Значит, в сумме останутся слагаемые по наборам, содержащим только единицы.

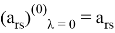
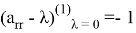
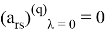
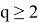
Рассмотрим сумму (3) при . Имеем:

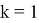
Раскрыв -й определитель по -й строке и -му столбцу, получим

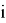
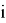
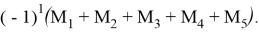
При в определителях будут две строки, содержащие (-1) и четыре 0. Раскрыв каждый определитель по этим строкам и столбцам, приходим к

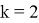
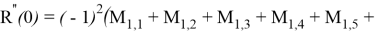
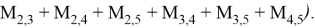
Аналогично получим выражения при и .

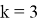
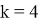
При

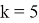
При каждый набор

содержит как минимум 2, поэтому определитель по ним равен 0.

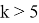
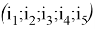
Подставив полученные выражения в (2), получим искомое утверждение.

Литература:

1. poivs.tsput.ru/ru/Math/Analysis/DifferentialEquations/FormulaLiouvilleOstrogradsky (дата обращения: 29.10.2023).

2. Кудрявцев Л. Д. Курс математического анализа в 3-х томах. Том 1: учебник для бакалавров. — 6-е изд., перераб. и доп. — М.: Изд-во Юрайт, 2023. — 703 с.