Векторы в геометрических задачах



В настоящей работе излагаются методы решения геометрических задач с использованием аппарата векторной алгебры. В отличие от большинства имеющихся задач, где основной акцент сделан на изучении и закреплении формальных операций над векторами, в данной работе основным является развитие у учащегося технических навыков на основе решения содержательных геометрических задач.

Задача 1 : Доказать, что медианы треугольника пересекаются в одной точке, которая делит каждую из медиан в отношении 2:1, считая от вершины.

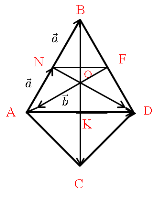
Доказательство:

В треугольнике точки F и N-середины сторон BD и AB соответственно, O-точка пересечения медиан AF и DN.

Введя , докажем, что ξ=η=2. Пусть = , тогда =2 , и = . По формуле деления отрезка DN точкой O в отношений ξ имеем

= . Следовательно, получим . Точка F делит отрезок DB в отношении 1:1, поэтому .Сравнивая полученные для вектора выражения, приходим к равенству

. В силу неколлинеарности векторов и отсюда следует, что .

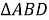
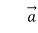
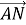
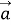
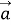
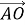
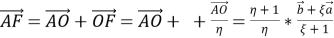
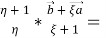
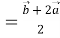
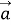
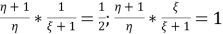
Разделив одно из этих равенств на другое, получим ξ=2. Следовательно , то есть η=2. Таким образом, доказано, что точка О, лежащая на медианк DN и делящая ее в отношении 2:1, лежит на медиане AF и делит ее в том же отношении. Аналогично можно установить, что та же самая точка O медианы DN лежит и на медиане BK и делит ее в отношении 2:1, считая от вершины B. Следовательно, все три медианы треугольника ABD пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.

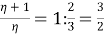
Задача 2: На сторонах CD и BC параллелограмма ABCD взяты точки N и K так, что , , где ξ и η — заданные положительные числа. Прямые ND и AK пересекаются в точке O. Найти отношение

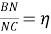
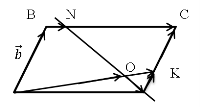
Решение :

Пусть ,

.

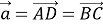
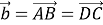
Тогда из равенств

находим, что .

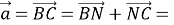
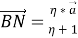
Аналогично имеем, . Таким образом, ; . Рассмотрим цикл AODA. По правилу цикла . (1)

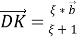
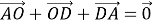
Здесь, векторы и неизвестны. Однако они коллинеарный векторам и соответственно, поэтому существуют такие неизвестные числа , что ; . Подставляя полученные выражения в равенство (1), имеем . Так как векторы и неколлинеарны, то получаем систему уравнений

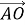
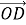
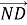
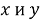
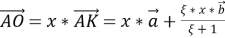
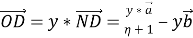
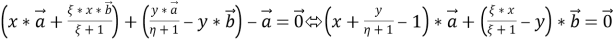
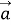
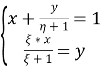
Решая ее, находим

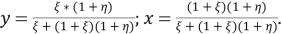
Таким образом

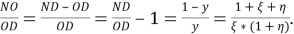
Задача 3: Доказать, что сумма квадратов длин диагоналей параллелограмма равна сумме квадратов длин всех его сторон.

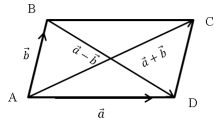
Доказательство :

Пусть и векторы сторон параллелограмма ABCD.

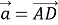
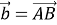
Тогда и есть векторы его диагоналей. Складывая почленно равенств ( и , получаем ( . (1) Поскольку и по формуле (1) получаем 2 2 2 2

2 2.

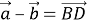
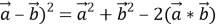
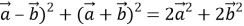
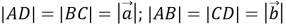
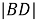
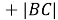
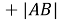
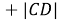
Задача 4: Выразите площадь треугольника через длины его сторон , , .

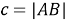
Решение:

Пусть , ,

, -площадь . По формуле имеем . Теперь, по формуле получил Следовательно .

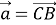
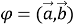
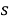
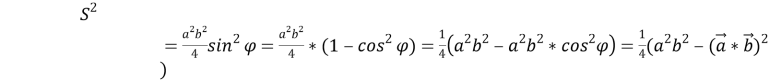
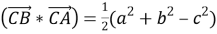
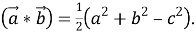
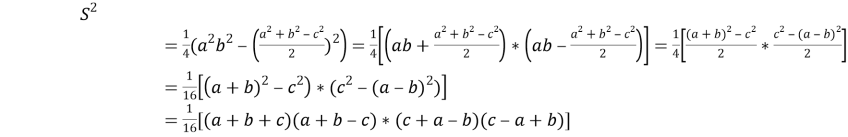
Здесь, если ввести обозначение , то получим Тогда имеем:

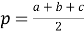
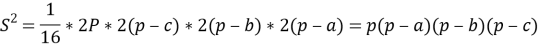
или т. е. получим формулу Герона, где — p полупериметр треугольника .

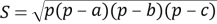
Задача 5: Доказать, что площадь трапеции равно , где и .

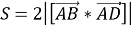
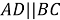
Доказательство :

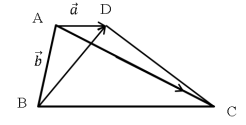
Обозначим . Тогда . Следовательно

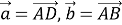
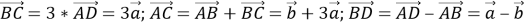
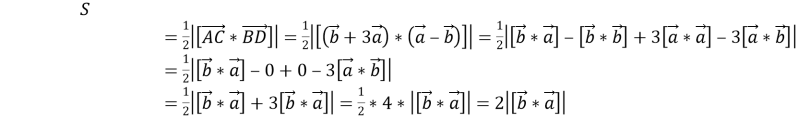
то есть получим

.

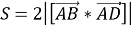
Литература:

1. Апанасов П. Т., Апанасов Н. П. Сборник математических задач с практическим содержанием: Книга для учителя. — М.: Просвещение, 1987г. — 110с.
2. Варданян С. С. Задачи по планиметрии с практическим содержанием: Книга для учащихся 6–8 кл. сред шк. /Под ред. В. А. Гусева — М.: Просвещение, 1989г. — 144с.
3. Киселев А. П. Элементарная геометрия. Книга для учителя. — Москва: Просвещение, 1980г. — 287с.