В статье автор рассматривает модель расслоения монодисперсной слабоконцентрированной эмульсии. Получена формула для оценки времени полного расслоения эмульсии на составляющие ее фазы.
Ключевые слова: эмульсия, расслоение, вязкость.
Эмульсии широко распространены во многих отраслях промышленности. В одних случаях необходимо, чтобы эмульсия не расслаивалась в течение длительного промежутка времени, в других, наоборот, требуется наискорейшее ее разрушение. Данное обстоятельство обуславливает необходимость разработки соответствующих математических моделей.
Будем характеризовать дисперсионную среду ее динамической вязкостью μ 1 , плотностью ρ 1 и объемом V 1 , а дисперсную фазу плотностью ρ 2 , размером капель d и объемом V 2 . Для определенности будем полагать, что дисперсная фаза — масло, а дисперсионная среда — вода, т. е. будем рассматривать прямую эмульсию. Геометрия сосуда определяется его высотой H и площадью поперечного сечения S (которая является постоянной).
Если принять, что все частицы имеют один размер, тогда общее число капель в эмульсии определяется из следующего соотношения:
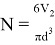
Предположение о равномерном распределении дисперсной фазы приводит к тому, что эмульсию можно рассматривать как множество кубических контейнеров, в каждом из которых находится капля и окружающая ее часть дисперсионной среды (рис. 1).
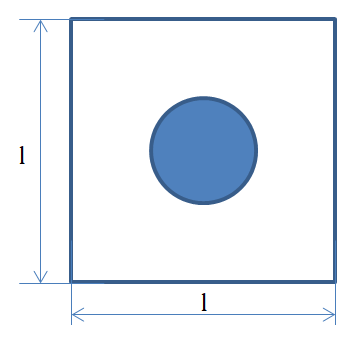
Рис. 1. Элементарная ячейка в эмульсии
Объемная концентрация дисперсной фазы с:
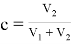
Тогда объем элементарной ячейки
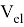
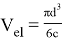
Следовательно, характерный линейный размер элементарной ячейки l:
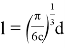
Тогда количество слоев в эмульсии N 1 =H/l, а количество ячеек в одном слое
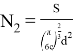
Рассмотрим случай, когда эмульсия не полностью заполняет сосуд, т. е. имеется воздушная прослойка (хотя ее наличие/отсутствие не влияет на разрушение эмульсии). В процессе расслоения прямой эмульсии будут сосуществовать три фазы: эмульсия, вода, масло (см. рис. 2).
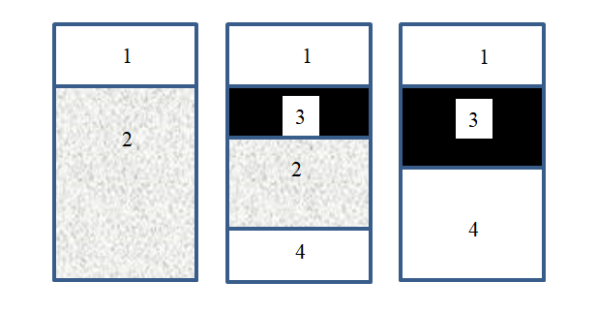
Рис. 2. Эмульсия в сосуде в разные моменты времени
(1 — воздух, 2 — эмульсия, 3 — масло, 4 — вода)
Коалесценция одного слоя капель приводит к увеличению слоя масла на величину h:
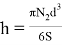
Примем, что коалесценция происходит, когда нижний край масляной капли достигнет границы раздела фаз. Следовательно, расстояние, которое пройдет самая первая капля, составит величину
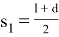
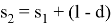
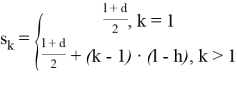
В формуле (6) k — номер слоя (максимальное значение N 1 ).
Время необходимое для коалесценции к-го слоя t k :
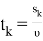
Скорость определяется из формулы Стокса
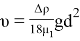
где g=9,8 м/с 2 , Δρ=ρ 1 -ρ 2 — разность плотностей.
Время полного расслоения эмульсии:
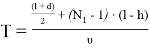
Полученное выражение отличается от простой оценки
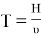
С целью удобства проведения расчетов объемы V 1 и V 2 можно выразить через объем всей эмульсии в начальный момент времени V и объемную концентрацию:
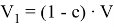
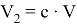
Полученные соотношения легко обобщить и на случай обратных эмульсий. Единственное отличие будет заключаться в том, что капли будут оседать, а не всплывать.
Поскольку наличие других частиц и влияние стенок сосуда вносят вклад в скорость всплытия [1] капель, то формула (8) будет справедлива для случая d<
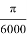
Таким образом, в представленной работе получена формула для оценки полного расслоения слабоконцентрированной эмульсии. Обобщение на более концентрированные системы требует введения поправок на скорость оседания/всплытия капель.
Литература:
1. Перепелкин К. Е., Матвеев В. С. Газовые эмульсии. — Химия. Ленингр. отд-ние, 1979.
2. Фридрихсберг Д. А. Курс коллоидной химии. — Рипол Классик, 1984.







