В работе [1] рассматривализадачи :
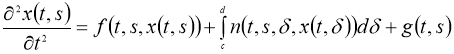

Доказали однозначную разрешимость.В данной работе рассматриваем следующую задачу:
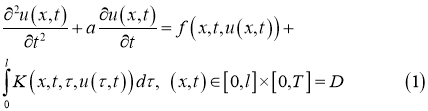
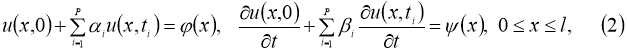
где
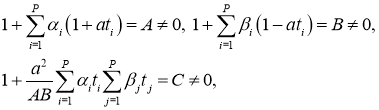
и находятся достаточные условия однозначной разрешимости.
- Задача однозначной разрешимости (1),(2)
Теорема 1.
Пустьфункции
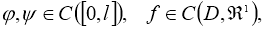
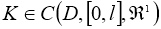
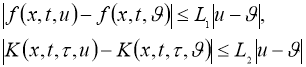
где L 1 ,L 2 = const ≥ 0,
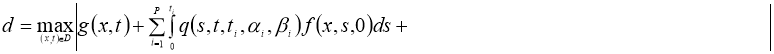
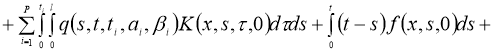

где
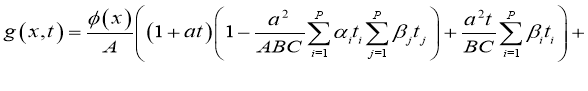
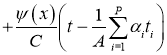
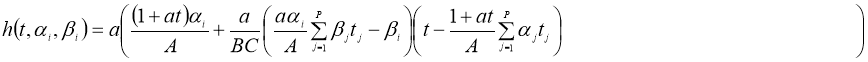
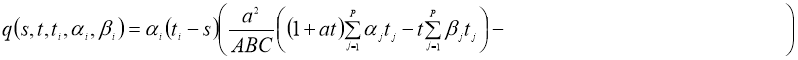
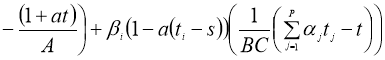
Если сушествует
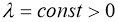
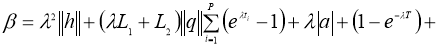

тогда задача (1), (2) имеет единственное решение U(x,t) в области D вместо непрерывной U tt
Доказательство . Легко можно доказать, что задача (1), (2) эквивалентна интегральному уравнению:
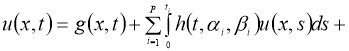
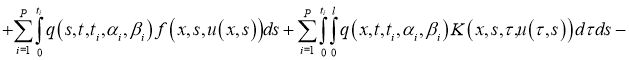
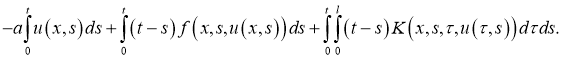
Правую часть этого уравнения обозначим через оператор Ф.
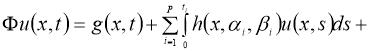
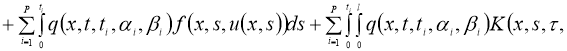
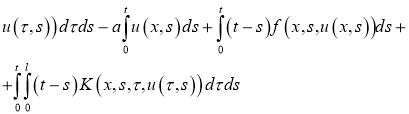
Очевидно, что
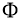
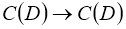
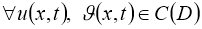
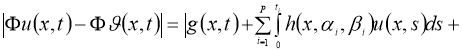
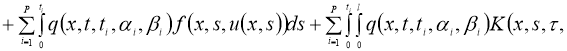
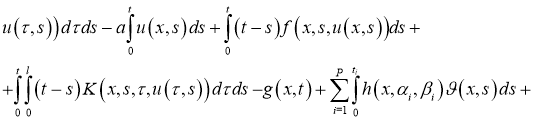
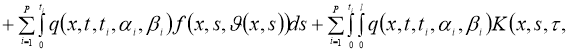
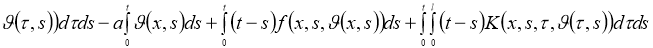
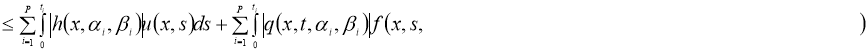
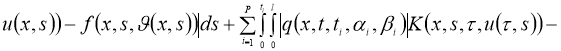
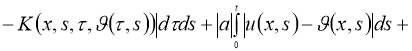
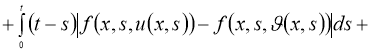
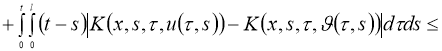
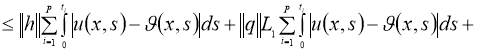
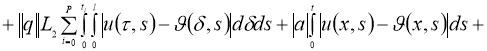
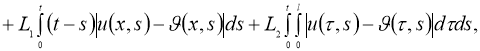
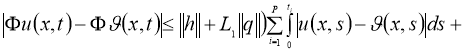
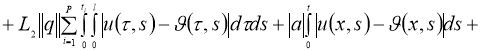
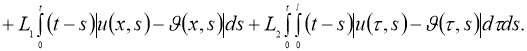
Используя норму
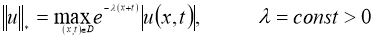
получим:
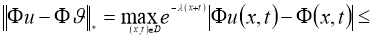
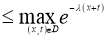
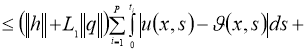
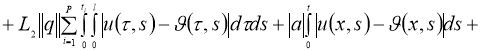
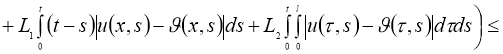
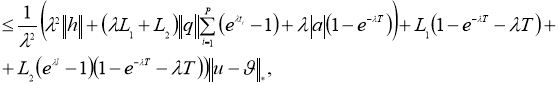
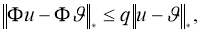
где
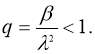
Доказательство теоремы следует из принципа сжимающих отображений.
- Непрерывная зависимость решения от параметров.
В этом пункте рассматривается следующая задача:
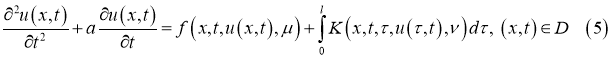
С условием (2), где
Теорема 2.
Пусть, функции
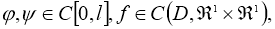
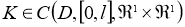
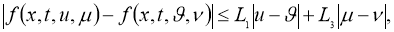
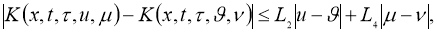
где
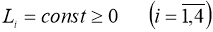
Если существует
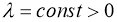
Доказательство . При фиксированных параметрах однозначной разрешимости задача (5), (2) доказана в теореме 1. Для доказательства теоремы 2 достаточно доказать непрерывную зависимость решения от параметров. Задача (5), (2) эквивалентна следующему интегральному уравнению:
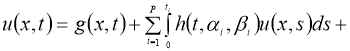
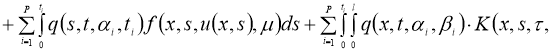
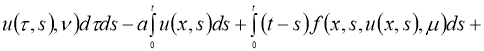

Обозначим через
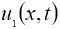
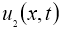
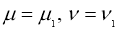
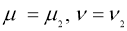
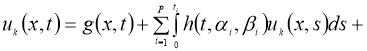
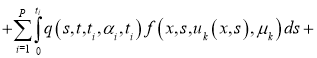
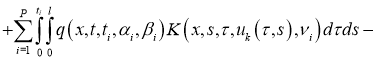
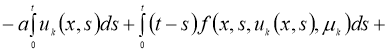
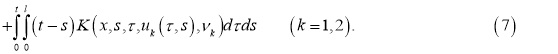
Используя условие теоремы 2, из (7) имеем:
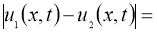
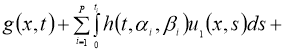
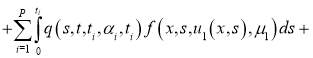
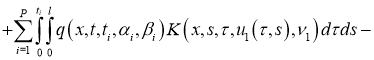
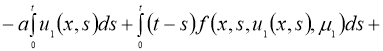
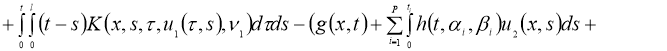
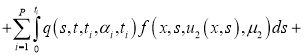
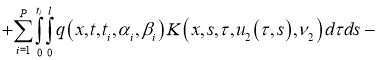
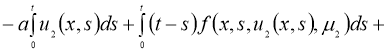
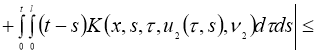
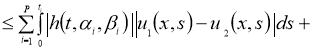
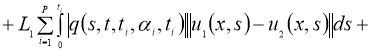
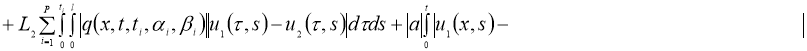
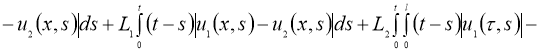
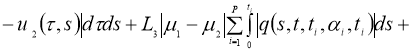
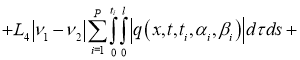
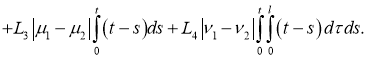
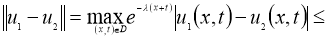

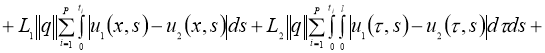
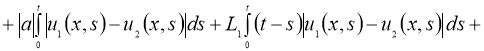
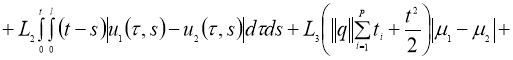
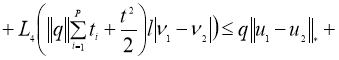
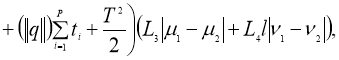
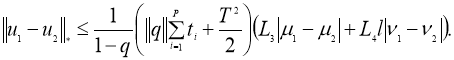
Отсюда следует утверждение теоремы 2.
Литература:
- Клатвин А. С., Клатвин В. А. Нелинейное интегро-дифференциальное уравнение Барвашина с частной производной второго порядка //Международная конференция ,,Современные методы и проблемы теории операторов и гармонического анализа и их приложения-VI” Ростов-на-Дону, 24–29 апреля 2016г.







