Данная статья посвящена численному исследованию собственных колебаний двухпролетных подтрибунных балок с неравными пролетами.
Ключевые слова: трибуны, балка переменного сечения, подтрибунные балки, балки-гребенки, шпангоуты, модальный анализ, собственные колебания, динамическая комфортность, оптимальное проектирование, стадион.
This article is devoted to the numerical study of natural vibrations of two-span under-tribune beams with unequal spans.
Keywords: stands, beam of variable section, sub-stand beams, ridge beams, frames, modal analysis, natural vibrations, dynamic comfort, optimal design, stadium.
Введение
Анализ проектов и литературы, посвященной проектированию стадионов [1÷16] показывает, что наиболее материало- и трудоемкими (как при проектировании, так и при выполнении строительных работ) элементами стадионов являются конструкции покрытия и трибуны.
В случае покрытий стадионов, как для стальных [1, 3], так и тентовых [4] конструкций, определяющими факторами являются снеговые и ветровые нагрузки.
В части конструкций трибун одним из определяющих факторов является снижение частот собственных колебаний конструкций, что достигается увеличением их изгибной жесткости, что так же приводит к увеличению их массы и расходу материалов. В ходе проектирования, с целью конструктивного оформления планировочных решений трибун (например, участки около лестничных клеток, перепадов по высоте поперечника стадиона и т. д.), не всегда удается обеспечить для конструкций подтрибунных балок наиболее рациональную схему работы [14]. Примером подобной ситуации является появление двухпролетных балок с разными пролетами, что предопределяет следующее:
- Сечение балки, подобранное по I и II группам предельных состояний, будет своим в каждом из пролетов.
- Одинаковые пролеты и жесткость сечения приводят к появлению одного «ведущего» пролета при определении частот и форм собственных колебаний.
Описание объекта исследования
Объектом исследования выбрана двухпролетная железобетонная подтрибунная балка с неравными пролетами.
Параметры (геометрия сечений и параметры материала) рассматриваемых балок принимаем аналогичными исследованию однопролетных балок [17]. Величина первого пролета составляет 4,725м, величина второго — варьируется. Так же варьируем следующие параметры:
— соотношение толщины плоской части балок к высоте ступеней: 1:1, 1.5:1; 2:1; 3:1; 4:1; 5:1; 6:1; 8:1; 10:1 (толщина плоской части от 135мм до 1350мм);
— соотношение пролетов балки к ширине «проступи» 7:1, 10:1; 15:1; 20:1; 27:1 (пролет балки от 2025мм до 8505мм);
— учет наличия ступеней в расчетной схеме заданием их в КЭ модели, либо только отдельной нагрузкой по верху балок.
В исследованиях двухпролетных балок постоянного сечения при действии сжимающей силы [19, 20] было установлено, что её наличие не оказывает существенного влияния на колебания балки. Таким образом, в данном исследовании влияние «скатной» составляющей собственного веса на частоты колебания балок так же опускаем. Расчетная схема принимается в виде горизонтальной двухпролетной неразрезной шарнирно опертой балки с неравными пролетами.
Описание численной модели
Построение КЭ схемы аналогично принятой в [17] для однопролетной балки, пример рассматриваемых КЭ моделей — рис. 1, рис. 2.

Рис. 1. КЭ схема двухпролетной подтрибунной балки пролетами 4,725м+2,205м с плоской частью толщиной 675мм (схема без учета ступеней, их вес задан отдельной нагрузкой)

Рис. 2. КЭ схема двухпролетной подтрибунной балки пролетами 4,725м+2,205м с плоской частью толщиной 675мм (схема с учетом ступеней)
Для дальнейшего анализа, как и в [17], используем безразмерный коэффициент K w . График зависимости коэффициента K w для различных толщин плоской части балок и величин пролетов балок приведен на рис. 3 и рис. 4.
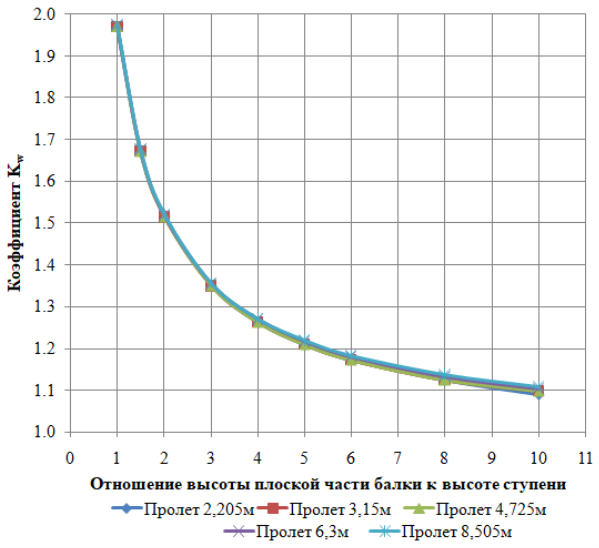
Рис. 3. Зависимость коэффициента K w от отношения высоты плоской части балки к высоте ступени
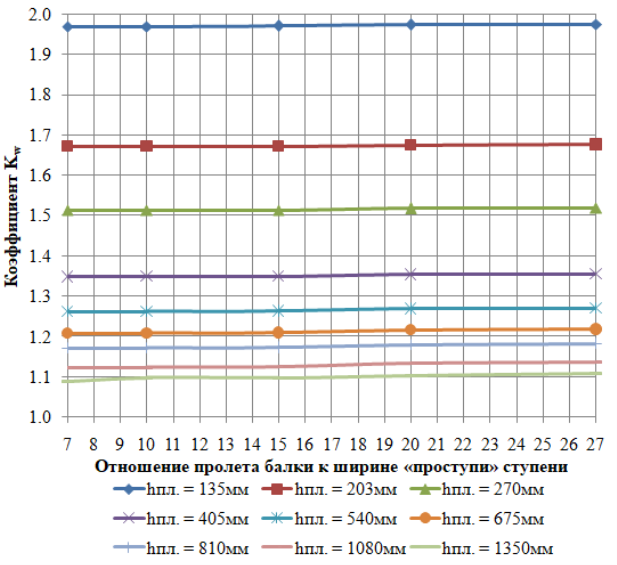
Рис. 4. Зависимость коэффициента K w от отношения пролета балки к ширине «проступи» ступени
Сравнение графиков рис. 3 и рис. 4 с аналогичными графиками для однопролетной балки [17] и однопролетной балки с консольным участком [18] показывает качественное сходство между рассматриваемыми зависимостями.
При этом, сравнение графиков зависимостей частоты собственных колебаний балок от отношения пролета балки к ширине «проступи» при одно- и двухпролетной схеме работы (см. рис. 5, рис. 6) показывает интересную закономерность.
![Зависимость частоты собственных колебаний однопролетной ступенчатой балки от отношения пролета балки к ширине «проступи» ступени (на основе данных [17])](https://moluch.ru/blmcbn/109341/109341.005.png)
Рис. 5. Зависимость частоты собственных колебаний однопролетной ступенчатой балки от отношения пролета балки к ширине «проступи» ступени (на основе данных [17])
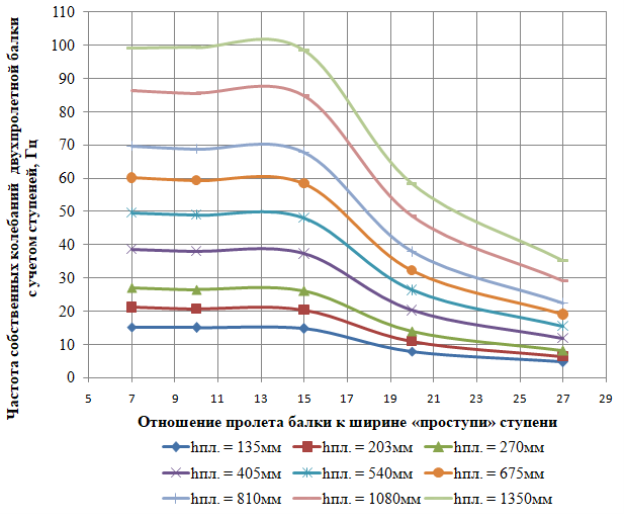
Рис. 6. Зависимость частоты собственных колебаний двухпролетной ступенчатой балки от отношения пролета балки к ширине «проступи» ступени
Как видно из рис. 6, для случая двухпролетной балки, при варьировании соотношения пролета балки к ширине проступи от 7 до 15, изменение частоты собственных колебаний почти не происходит, а при увеличении пролета, наблюдается вновь отчетливая нелинейная зависимость.
Выводы
- Произведен модальный анализ 90 расчетных схем двухпролетных подтрибунных балок с неравными пролетами для различных высот плоской части и пролетов при постоянных размерах ступеней.
- Для коэффициентов K w получены те же зависимости от геометрии балок, как и в случае однопролетных балок [17, 18].
- Выявлено, что при определенных соотношениях пролета балок к ширине проступи (от 7-ми до 15-ти кратной) частота собственных балок является практически одинаковой.
Литература:
1. Вариантное проектирование покрытия стадиона «ФИШТ» в городе Сочи / И. А. Порываев, А. А. Семенов, Р. Р. Шигапов [и др.] // Строительство уникальных зданий и сооружений. — 2016. — № 6(45). — С. 7–33. — EDN WEFRCT.
2. Испытание натурных узлов конструкции увеличения козырька покрытия БСА «Лужники» / М. И. Гукова, М. И. Фарфель, С. В. Гуров [и др.] // Строительная механика и расчет сооружений. — 2015. — № 3(260). — С. 63–69. — EDN UABYSB.
3. Поиск рациональной геометрической схемы пространственной металлической конструкции покрытия большепролетного спортивного сооружения / М. Р. Гарифуллин, С. А. Семенов, С. В. Беляева [и др.] // Строительство уникальных зданий и сооружений. — 2014. — № 2(17). — С. 107–124. — EDN RWGNQF.
4. Валеева, А. Р. Работа тентового покрытия в ветровом потоке / А. Р. Валеева // Тезисы докладов 70-й Международной научной конференции по проблемам архитектуры и строительства. — Казань: Издательство КГАСУ. — 2018. — С. 66.
5. Ганина, Т. С. Организация рабочего процесса проектирования объекта БСА «Лужники»/ Т. С. Ганина // АО «Казанский Гипронииавиапром» «Новое в архитектуре, проектировании строительных конструкций и реконструкции: материалы научно-практической конференции 2016, в честь 75-ти летия предприятия». — 2016 — С. 136–143.
6. Гранев, В. В. Особенности конструктивных решений футбольного стадиона на 45000 зрителей в Ростове-на-Дону / В. В. Гранев, Н. Г. Келасьев // Деловая слава России. — 2015. — № 50. — С. 28–30. — EDN VOBXCX.
7. Гранев, В. В. Научная и проектная деятельность ЦНИИПромзданий в области строительства многофункциональных комплексов / В. В. Гранев, Д. К. Лейкина // Промышленное и гражданское строительство. — 2009. — № 8. — С. 15–17. — EDN KUAFSV.
8. Келасьев, Н. Г. Опыт проектирования и строительства футбольного стадиона на 45 000 зрителей в г. Казани / Н. Г. Келасьев, И. В. Келасьева // Бетон и железобетон — взгляд в будущее: научные труды III Всероссийской (II Международной) конференции по бетону и железобетону: В семи томах, Москва, 12–16 мая 2014 года. Том 2. — Москва: Московский государственный строительный университет, 2014. — С. 287–295. — EDN UBXDRP.
9. Келасьев, Н. Г. Экспериментальные исследования сборных конструкций настила трибун футбольного стадиона на 45 000 зрителей в Ростове-на-Дону / Н. Г. Келасьев, К. В. Авдеев // Промышленное и гражданское строительство. — 2016. — № 6. — С. 20–24.– EDN WAIEIR.
10. Лейкина, Д. Проектирование стадионов для Чемпионата мира по футболу 2018 / Д. Лейкина // Архитектура. Строительство. Дизайн. — 2011. — № 1(62). — С. 30–33. — EDN NTKYAD.
11. Максутов, Т. Р. Опыт проектирования каркаса БСА «Лужники»/ Т. Р. Максутов // АО «Казанский Гипронииавиапром» «Новое в архитектуре, проектировании строительных конструкций и реконструкции: материалы научно-практической конференции 2016, в честь 75-ти летия предприятия». — 2016 — С. 85–95.
12. Назаров, Ю. П. Анализ динамической реакции трибун спортивных сооружений на согласованные действия зрителей / Ю. П. Назаров, Е. В. Позняк // Фундаментальные, поисковые и прикладные исследования РААСН по научному обеспечению развития архитектуры, градостроительства и строительной отрасли Российской Федерации в 2015 году: Сборник научных трудов РААСН / Российская академия архитектуры и строительных наук. — Москва: Издательство АСВ, 2016. — С. 543–547. — EDN ZBTEWI.
13. Нысанбаева, А. С. Стадиондардың сәулеттік-жоспарлау шешімдерін қалыптастыру ерекшеліктері / А. С. Нысанбаева // Актуальные научные исследования в современном мире. — 2021. — No. 3–5(71). — P. 34–39. — EDN XGTTWJ.
14. Трофимов, Д. П. Проектирование монолитных железобетонных балок-гребенок для установки трибун при реконструкции Большой спортивной арены «Лужники» к Чемпионату мира по футболу 2018г. / Д. П. Трофимов // Тезисы докладов 69-й Международной научной конференции по проблемам архитектуры и строительства. — Казань: Издательство КГАСУ. — 2017. — С. 26.
15. Фарфель, М. И. Обеспечение безаварийной эксплуатации уникального большепролетного покрытия Большой спортивной арены олимпийского стадиона «Лужники» / М. И. Фарфель // Строительная механика и расчет сооружений. — 2012. — № 6(245). — С. 56–61. — EDN PJQXZV.
16. Ярков, И. Д. Конструктивные особенности Олимпийского стадиона «Фишт» Г. Сочи / И. Д. Ярков // Дни студенческой науки: Сборник докладов научно-технической конференции по итогам научно-исследовательских работ студентов института строительства и архитектуры, Москва, 12–16 марта 2018 года / Министерство образования и науки Российской Федерации, Национальный исследовательский Московский государственный строительный университет. — Москва: Национальный исследовательский Московский государственный строительный университет, 2018. — С. 1474–1476. — EDN XTTGHR.
17. Трофимов, Д. П. Численное исследование собственных колебаний однопролетных подтрибунных балок / Д. П. Трофимов, Э. Р. Аджихай. — Текст: непосредственный // Молодой ученый. — 2022. — № 31 (426). — С. 19–24. — URL: https://moluch.ru/archive/426/94289/ (дата обращения: 17.12.2023). — EDN LPQAVB.
18. Трофимов, Д. П. Численное исследование собственных колебаний однопролетных подтрибунных балок с консольным участком / Д. П. Трофимов // Исследования молодых ученых: материалы XLV Международной научной конференции, Казань, 20–23 октября 2022 года. — Казань: Общество с ограниченной ответственностью «Издательство Молодой ученый», 2022. — С. 8–15. — URL: https://moluch.ru/conf/stud/archive/460/17461/ (дата обращения: 17.12.2023). — EDN ZAITSV.
19. Zingales U., Elishakoff I. Localization of the bending response in presence of axial load // International Journal of Solids and Structures. — 2000. — Volume 37, Issue 45. — p. 6739–6753. https://doi.org/10.1016/S0020–7683(99)00282–6.
20. Кельин, В. А. Свободные колебания сжатой двухпролетной балки в случае смещения внутренней упругой опоры / В. А. Кельин. — Текст: непосредственный // Сборник работ 70-ой научной конференции студентов и аспирантов Белорусского государственного университета, 15–18 мая 2013 г., В 3 ч. Ч. 1. — Минск: Изд. центр БГУ, 2012. — С. 109–110. — URL: https://elib.bsu.by/handle/123456789/95112 (дата обращения: 17.12.2023).







