Месторождение находится на территории Красноселькупского района Ямало-Ненецкого автономного округа Тюменской области. Характерной особенностью района работ является наличие вечной мерзлоты. Исследуемый участок относится к южной части Тазовской области массивно-островного и островного распространения ММП и талых пород с островами и перелётами. В географическом отношении месторождение расположено в северо-восточной части Западно-Сибирской равнины, в южной части Пурской низменности и представляет собой пологоволнистую равнину с абсолютными отметками рельефа от +50 м в долинах рек и до +180 м на водоразделах. Рельеф поверхности холмисто-увалистый.
Геологические модели представляют собой трехмерные массивы данных, характеризующие структурные, литологические, фильтрационные, емкостные характеристики, а также характер насыщения коллекторов продуктивных пластов.
Методологическая основа формирования трехмерных геологических моделей в работе принципиально не отличается от общепринятых правил геометризации геологических тел, определения фильтрационно-емкостных свойств коллекторов и характера их насыщения. Поэтому наиболее важными критериями адекватности компьютерных моделей реальным геологическим объектам служили их соответствия по распределениям основных геометрических, емкостных и фильтрационных характеристик, а также по средним значениям объемов, емкости, насыщенности и величине запасов нефти с аналогичными параметрами.
Для построения данной модели послужили результаты попластовой интерпретации данных ГИС и петрофизические зависимости, обоснованные на данных исследований керна.
Перед пространственным распределением параметра пористости на основе скважинных данных создавались двухмерные тренды.
Создание модели пористости выполнялось в 2 этапа. Поскольку область моделирования разбурена неплотной сеткой скважин, то в качестве алгоритма интерполяции использовался стохастический метод Sequential Gaussian Simulation. Распределение пористости осуществлялось в коллекторе, в неколлекторе задавался ноль. Использовались настройки моделирования, аналогичные параметру литологии. В качестве трендов использовались карты, построенные по скважинным данным и ГСР, объединенные в единый трендовый куб.
На первом этапе рассчитывалось 5 равновероятных реализаций с учетом указанных выше настроек и трендов. На втором этапе полученные реализации усреднялись в финальный куб пористости. Использование нескольких реализаций с последующим осреднением позволяет существенно уменьшить шум, свойственный всем стохастическим методам интерполяции. Выбор 5 реализаций позволяет в достаточной степени решить данную задачу. Использование заметно большего количества реализаций приводит к результату, близкому к получаемому при применении детерминистского метода Kriging, который рекомендуется использовать при плотной сетке скважин.
Коэффициенты корреляции между трендовыми картами пористости и картами, полученными с куба пористости, составили 0,95. На рисунках 1 и 2 приведены кросс-плоты сопоставления карт. Финальный куб пористости представлен на рисунке 3.
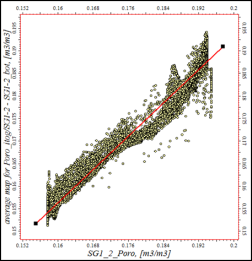
Рис. 1. Кросс-плот карт параметра пористости полученных с трехмерного куба и карты, использовавшейся в качестве тренда для пласта X
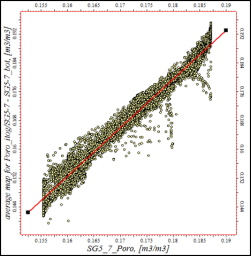
Рис. 2. Кросс-плот карт параметра пористости полученных с трехмерного куба карты, использовавшейся в качестве тренда для пласта Y
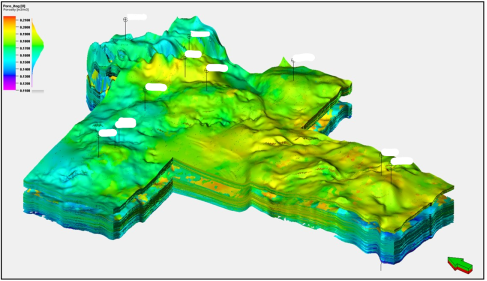
Рис. 3. Итоговый куб пористости для пластов X и Y
Модель проницаемости получена на основе петрофизической зависимости от пористости, созданной на основе стандартных исследований керна [1].
Построение модели нефтенасыщенности осуществлялось на основе данных попластовой интерпретации ГИС и модели переходной зоны, созданной на основе данных капиллярометрических исследований керна.
Для создания модели переходной зоны обобщены результаты капиллярометрических исследований по двум скважинам. J-функция Леверетта рассчитывалась по формуле:
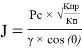
где:
Рс — величина капиллярного давления,
Kпр — коэффициент проницаемости,
Kп — коэффициент пористости,
γ — поверхностное натяжение углеводороды/пластовая вода,
θ — угол смачиваемости.
Все величины, участвующие в расчетах, переведены в систему СИ. Расчеты выполнялись в стандартных условиях. Поверхностное натяжение на границах раздела нефть-вода — константа и равна 45 дин/см. Угол смачиваемости θ=30. Результирующая зависимость водонасыщенности от J-функции Леверетта для пласта Х получилась:
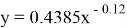
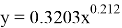
Далее с помощью полученной зависимости, с учетом параметров пористости, проницаемости и капиллярного давлении, восстанавливался куб водонасыщенности, расчет проводился для пластовых условий. Далее при распределении параметра нефтенасыщенности задавался трендовый куб, полученный как 1-Кв [2]. Итоговый куб нефтенасыщенности представлен на рисунке 4.
Таблица 1
Значения коэффициентов для расчета J−функции в пластовых условиях
|
Система нефть-вода |
|
|
Угол смачивания θ, град |
30 |
|
Межфазное натяжение, дин/cм |
30 |
|
γ ×cos θ |
26 |
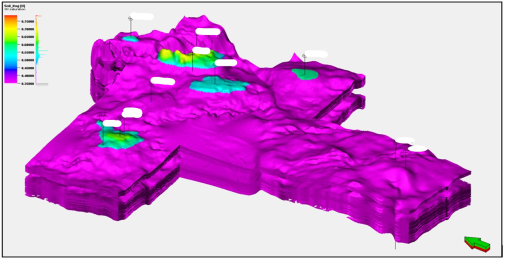
Рис. 4. Итоговый куб нефтенасыщенности для пластов X и Y
Полученный куб нефтенасыщенности позволил определить, что средняя нефтенасыщенность для пластов X и Y составляет порядка 0.5–0.6 д.ед. Вышеизложенная информация может помочь принять верное решение в оптимизации добычи углеводородного сырья.
Литература:
- Мищенко И. Т. Скважинная добыча нефти: Учебное пособие для вузов. — М.: ФГУП Изд-во «Нефть и газ» РГУ нефти и газа им. И. М. Губкина, 2013. — 816 с.
- Схема нефтегазогеологического районирования Западно-Сибирской нефтегазоносной провинции (под редакцией А. Э. Конторовича (2004 г.) с дополнениями А. В. Рылькова, Н. Х. Кулахметова, В. В. Потеряева)







