В данной статье рассмотрено применение известного из стереометрии метода объемов для решения практической задачи строительного проектирования — определения вертикального перемещения грунта, находящегося на бровке шпунтового ограждения котлована.
Ключевые слова: котлован, ограждение котлована, гибкая подпорная стена, шпунтовое ограждение, стереометрия, метод объемов.
This article discusses the use of the volume method, known from stereometry, to solve a practical problem in construction design — determining the vertical movement of soil located on the edge of the sheet piling of a pit.
Keywords: pit, pit fencing, flexible retaining wall, sheet piling, stereometry, volume method.
Рассматривается задача по проектированию котлована для устройства подземного резервуара. При этом, в зоне выполнения земляных работ расположена действующая железнодорожная линия. С целью сохранения железнодорожного пути, и возможности его использования в ходе строительных работ, ограждение ближней к пути стенки котлована было запроектировано в виде гибкой подпорной стенки из шпунта Ларсена (далее по тексту — шпунтовое ограждение). Основные параметры ограждения приведены на рис. 1 и рис. 2.
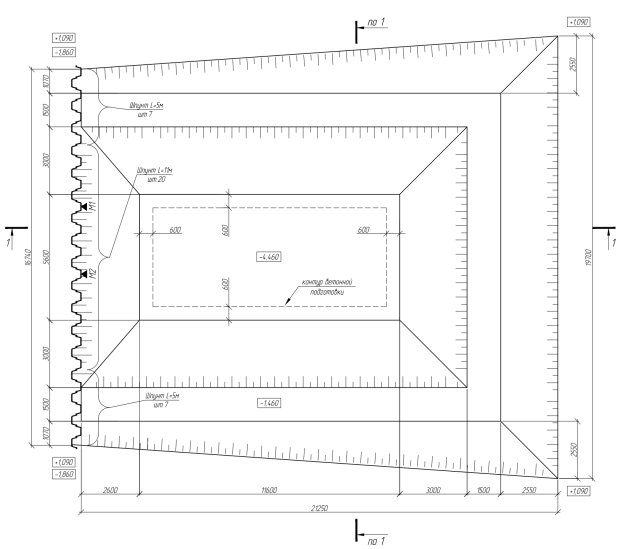
Рис. 1. Схема котлована и шпунтового ограждения (М1, М2 — марки геотехнического мониторинга)
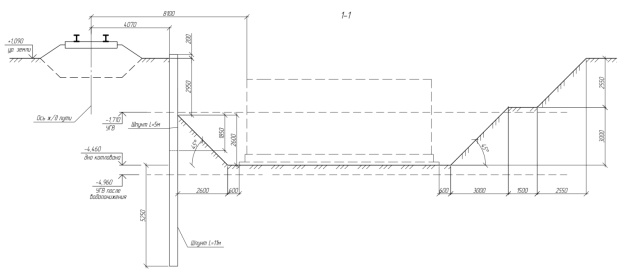
Рис. 2. Сечение по котловану и шпунтовому ограждению
Положение шпунтового ограждения в плане принято по указаниям [5, п. 6.23] и обеспечивает сохранность балластного слоя железнодорожного пути на весь период строительства. В соответствии с указаниями [2–5] был произведен сбор нагрузок, действующих на шпунтовое ограждение, и выполнен его расчет. По результатам расчета было определено сечение шпунта (тип Л5-У) и величина его заделки в грунт (см. рис. 2).
В ходе дальнейшего расчета было необходимо определить вертикальную деформацию земляного полотна пути и сравнить её с предельно допустимым значением. Из анализа требований [1, табл. 3], для рассматриваемого пути величина предельно деформации составила 3 мм.
При этом, нормативные и справочные документы по проектированию подпорных стен рассматривают и ограничивают лишь горизонтальное перемещение верха подпорных стен (например [5, п. 6.23]), но не рассматривают вертикальные деформации грунта в зоне бровки.
Точная оценка вертикальных деформаций грунта в зоне бровки подпорных стен требует геотехнического расчета. При этом, предварительную оценку деформаций можно провести, рассмотрев решение стереометрической задачи с помощью метода объемов [6, 7].
Для решения задачи, задаемся следующим условием: объем грунта, получающий горизонтальное перемещение от прогиба ограждения (получено из расчета шпунта и составляет 4мм), равен объему грунта, получающему при этом вертикальное перемещение (рис. 3).
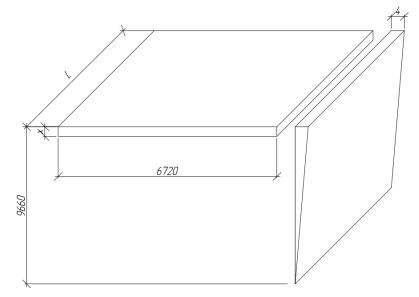
Рис. 3. Схема к определению вертикальных деформаций грунта в зоне бровки шпунтового ограждения (6720мм — ширина участка от грани шпунта до крайней точки балластного слоя; 9660мм — длина шпунта)
На основе рис. 3 составляется пропорция равных объемов параллелепипеда и призмы, из которой следует, что размер «x» (вертикальное перемещение балластного слоя вместе с ж/д полотном) при горизонтальном перемещении верха ограждения 4 мм составит 2,9 мм (при предельной — 3,0мм).
Таким образом, примененный метод объемов позволил без применения программ геотехнического расчета предварительно определить порядок величины вертикального перемещения (деформации) грунта в зоне бровки шпунтового ограждения.
Литература:
1. СП 238.1326000.2015. Железнодорожный путь. М.: Минтранс России, 2015.
2. СП 20.13330.2011 Нагрузки и воздействия Актуализированная редакция СНиП 2.01.07–85*
3. СП 43.13330.2012 Сооружения промышленных предприятий. Актуализированная редакция СНиП 2.09.03–85
4. СП 381.1325800.2018 Сооружения подпорные. Правила проектирования
5. Справочное пособие к СНиП 2.09.03–85 «Проектирование подпорных стен и стен подвалов» / ЦНИИпромзданий — М.: Стройиздат, 1990
6. Готман, Э. Г. Стереометрические задачи и методы их решения / Э. Г. Готман. — М.: МЦНМО, 2006. — 160 c.: ISBN: 5–94057–263–4
7. Любимова, В. В. Метод объёмов как удобный способ решения стереометрических задач / В. В. Любимова // Математика в школе. — 2019. — № 3. — С. 27–35. — EDN ZKHLDQ.







