Создание математических моделей, описывающих поведение высокопрочных бетонов и железобетонных элементов из них требует тщательной подготовки исходных данных. Кроме того, пространственная работа высокопрочного бетона выражается нелинейными функциями, от точности учета которых зависит конечный результат математического моделирования. В данной статье предлагается подход к моделированию элементов с использованием высокопрочного бетона через условное разрушение.
Ключевые слова: высокопрочный бетон, железобетон, прочность бетона, испытания высокопрочного бетона, математическое моделирование высокопрочного бетона.
The creation of mathematical models describing the behavior of high-strength concrete and reinforced concrete elements from them requires careful preparation of initial data. In addition, the spatial work of high-strength concrete is expressed by nonlinear functions, the accuracy of which determines the final result of mathematical modeling. This article proposes an approach to modeling elements using high-strength concrete through conditional destruction.
Keywords: HPC, reinforced concrete, concrete strength, testing of high-strength concrete, mathematical modeling of high-strength concrete.
Введение
Структурный анализ и верификация требуют уточнения параметров прочности материала. Эти параметры подвержены неопределенности, которую необходимо учитывать при анализе. Во многих случаях для учета этой неопределенности используется консервативное характерное значение [1, 2, 3].
При этом современные расчетные комплексы позволяют проводить глубокий анализ с учетом механики разрушения. Однако такой расчет требует достаточно больших вычислительных ресурсов, соответственно, использование моделей, поддерживающих механику разрушения целесообразно на лабораторных образцах. Для моделирование больших конструкций требуется упрощать расчетную модель.
Критерии условного разрушения
Высокопрочный бетон является нелинейным материалом, и для того, чтобы добиться точного моделирования поведения конструкции или её элементов проявление нелинейности требуется сохранить, однако полная механика разрушения (образование трещин и т. д.) требует большого количества элементов в расчетной модели, более качественной подготовки сетки и деления стадий расчета на большее количество итераций.
Как правило, эксперименты с бетоном или железобетоном предполагают доведение образца до разрушения. При этом, бетон сам по себе является сложным материалом, который во-первых анизотропен, во-вторых проявляет ярко выраженную нелинейность.
Таким образом моделирование объединяет в себе:
— экспериментальные данные;
— принятую модель материала;
— теоретические данные, полученные из нормативной документации.
В данной работе предлагается использование модели бетона Drucker-Prager в введение следующих критериев, которые можно считать началом разрушения:
— достижение предельных относительных деформаций при растяжении;
— достижение максимального нормального напряжения при сжатии.
С помощью такого подхода автором в рамках численного эксперимента были верифицированы данные физических экспериментов. Ниже показаны результаты испытаний стандартных образцов на сжатие, а также результаты, полученные при моделировании стандартного образца из высокопрочного бетона класса В100 (при этом в модели использованы нормативные данные соответствующие СП63.13330).
В ходе расчета установлено, что максимальное сжимающее напряжение в образце достигло своего пика -79 МПа, при этом результаты экспериментов устанавливают диапазон значений -75..-80 МПа. Относительная деформация при этом составляет: e b0 =0,4/150=0,00266. Т. е. разница между теоретическим значением и значением, полученным в результате эксперимента, составляет 9 %.
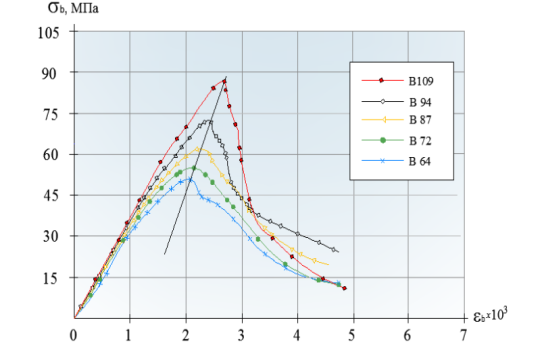
Рис. 1. Результаты испытаний стандартных образцов из высокопрочного бетона
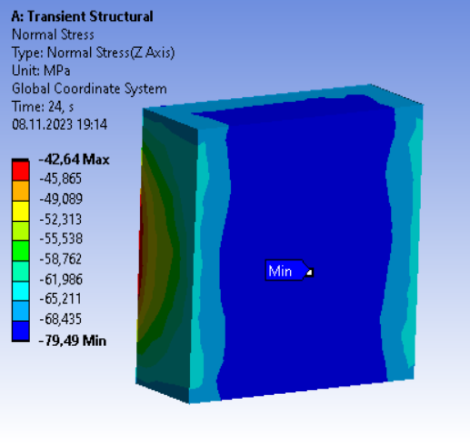
Рис. 2. НДС образца при пиковом напряжении, МПа
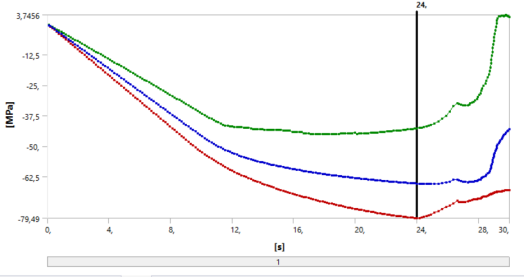
Рис. 3. Зависимость напряжения от величины нагрузки, МПа
В случае с растяжение данный подход позволяет в результате расчета определить область формирования трещин. Ниже показаны результаты численного эксперимента, повторяющего испытания балки на четырехточечный изгиб.
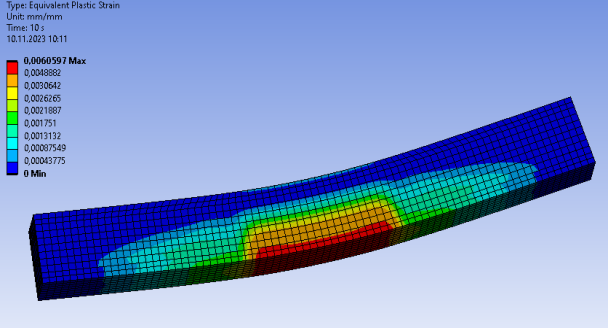
Рис. 4. Пластические деформации при максимальной нагрузке
В данном случае механика модели не предполагает образование трещин в виде отдельных структур, бетон с трещинами выключается из работы согласно графику разупрочнения с нарастанием пластических деформаций, образование и раскрытие трещин происходи в растянутой зоне с относительной деформацией более 0,000176.
Выводы
Предложенный подход с введением условных критериев разрушения и использование модели Drucker-Prager для моделирования железобетонных элементов из высокопрочного бетона способен привести к оптимизации расчетных моделей и при этом проводить расчеты до момента начала разрушения.
Литература:
- Aitcin, P. C. High Performance Concrete, 1998.
- Nawy, Edward G. Fundamentals of High Strength High Performance Concrete, 1996.
- Peterman, M.B. & Carrasquillo,R. L. Production of High Strength Concrete, 1986.
- Мкртчян А. М., Маилян Д. Р. Влияние разных факторов на работу железобетонных колонн из высокопрочных бетонов // Интернет-журнал Науковедение. 2013. № 5(18). С. 117.
- Мкртчян А. М., Аксенов В. Н. Аналитическое описание диаграммы деформирования высокопрочных бетонов // Инженерный вестник Дона. 2013. Т. 26. № 3(26). С. 127.
- Аксенов В. Н., Аксенов Н. Б., Блягоз А. М., Хутыз А. М. Особенности конструктивных свойств высокопрочных бетонов // https://cyberleninka.ru/article/n/osobennosti-konstruktivnyh-svoystv-vysokoprochnyh-betonov?ysclid=loq4omd2r0247260629







