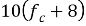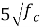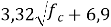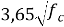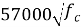Разработка технологий производства балок из высокопрочного бетона (HPC) с целью создания безопасного и долговечного материала тесно связана с численными моделями реальных объектов. В работе исследованы трехмерные нелинейные конечно-элементные модели армированных высокопрочных бетонных балок со сложной геометрией. Численный анализ выполнен с использованием конечно-элементного пакета ANSYS. Сравнение результатов свидетельствует о правильности критериев разрушения, принятых для высокопрочного бетона и стальной арматуры. Результаты численного моделирования чувствительны к модулю упругости и коэффициенту передачи сдвига для открытой трещины, присвоенному высокопрочному бетону. Полные нелинейные кривые нагрузки-прогиба в середине пролета балок, развитие деформации в сжимаемом бетоне и развитие деформации в растягивающем стержне хорошо согласуются с экспериментальными результатами.
Ключевые слова: высокопрочный бетон, метод конечных элементов, армированные высокопрочные бетонные балки, моделирование.
The development of technologies for the production of beams made of high-strength concrete (HPC) in order to create a safe and durable material is closely related to numerical models of real objects. The paper investigates three-dimensional nonlinear finite element models of reinforced high-strength concrete beams with complex geometry. The numerical analysis was performed using the ANSYS finite element package. A comparison of the results indicates the correctness of the fracture criteria adopted for high-strength concrete and steel reinforcement. The numerical simulation results are sensitive to the modulus of elasticity and shear transfer coefficient for an open crack assigned to high-strength concrete. The complete nonlinear load-deflection curves in the middle of the beam span, the development of deformation in compressible concrete and the development of deformation in a tensile rod are in good agreement with experimental results.
Keywords: HPC, finite element method, reinforced high-strength concrete beams, modeling.
Введение
Повышение производительности вычислительных систем и возможность их использования при проектировании инженерных сооружений стимулируют интенсивное развитие численных методов анализа статического и динамического поведения конструкций. Численные методы — единственный способ получить полезные решения для сложных пространственных конструкций, изготовленных из материалов, ведущих себя нелинейно, как бетон. Влияние прочности бетона на сжатие и изгиб влияние коэффициента усиления при растяжении на поведение при прогибе под нагрузкой и пластичность армированных высокопрочных бетонных балок было описано несколькими предыдущими исследователями [1–3]. Усиленные элементы HPC требовали не только экспериментальных испытаний, но и конечно-элементного моделирования поведения при разрушении. Немногие исследователи изучали конечно-элементное моделирование железобетонных балок [4–5] с использованием пакет конечных элементов ANSYS. Однако доступные публикации по исследованию методом конечных элементов армированных высокопрочных бетонных балок по-прежнему ограничены.
Описание предельного состояния бетона при статическом нагружении было предметом многочисленных публикаций. Уравнения предельной поверхности для бетона описаны в статье [3]. Предложенные уравнения предельной поверхности зависят от первого инварианта тензора напряжений и второго, и третий инвариант девиатора напряжений. Это описание позволяет наиболее точно аппроксимировать конкретные экспериментальные результаты в сложном напряженном состоянии. Сфокусируемся на уравнении предельной поверхности в зависимости от пяти параметров напряжений в соответствии с [4] и введем закон изменения предельной поверхности. Критерий разрушения бетона в сложном напряженном состоянии описывается следующим уравнением:
Fa / fc = Sa, a = 1,,4 (1)
в котором: Fa — функция условий нормальных напряжений σxp, σyp, σzp в направлении декартовой система координат xyz, Sa — поверхность разрушения, зависящая от главных напряжений σ1, σ2, σ3, где: σ1 = max(σxp, σyp, σzp), σ3 = min(σxp, σyp, σzp), σ1 ≥ σ2 ≥ σ3, и параметры прочности: fc — прочность на одноосное сжатие, вызывающее раздавливание, ft — предел прочности при одноосном растяжении, fcb — предельная прочность при двухосном сжатии, f1 — предел прочности при сжатии для состояния двухосного сжатия, наложенного в состоянии гидростатического напряжения σha, f2 — предел прочности при сжатии для состояния одноосного сжатия, наложенного в состоянии гидростатического напряжения σha.
Предельная поверхность с законом эволюции используется в качестве критерия разрушения бетона в соответствии со следующей интерпретацией. Материал поврежден, если выполняется уравнение 1. Состояние разрушения можно определить как состояние растрескивания, если какое-либо основное напряжение является растягивающим. В противном случае его можно определить как состояние разрушения, если все основные напряжения являются сжимающими. Эволюция предельной поверхности определяется предложенным законом твердения/размягчения, показанным на рисунке 1. Зависимость напряжения от деформации при одноосном сжатии подтверждается экспериментальными наблюдениями, показывающими гораздо большую предельную деформацию бетона в конструкции, чем в образце. Отметим, что использование соотношения напряжение-деформация, основанного на коде модели 90, приводит к значительному снижению предельного прогиба балки.
Более того, результаты экспериментов показали, что низкая пластичность высокопрочного бетона в конструктивных элементах не оправдано, поскольку деформации достигали 6–12‰ [6,7]. Предполагалось линейное соотношение напряжение-деформация для одноосного сжатия на уровне 0,3fc. Затем начинается область упругопластического упрочнения с линейным увеличением напряжения вплоть до предела прочности при одноосном сжатии fc. После этого напряжения в бетоне уменьшаются до 0,8fc при предельной деформации ecu. Предполагалась деформация ec1 = 6‰ при fc и предельные деформации сжатия ecu = 12‰. Кривая зависимости напряжения от деформации при растяжении бетона представляет собой линейный вплоть до предела прочности при растяжении ft (см. рис. 1б). Предполагается, что модуль упругости при растяжении равен модулю упругости при сжатии. После достижения ft растягивающее напряжение внезапно уменьшается до значения Tcft.
Параметр Tc следует выбирать из диапазона 0,6 ≤ Tc ≤ 1. Эффект придания жесткости показывает постепенное снижение предела прочности при растяжении до нуля и описывается деформацией, равной 0,8‰, если Tc = 0,6, или 1,4‰, если Tc = 1.
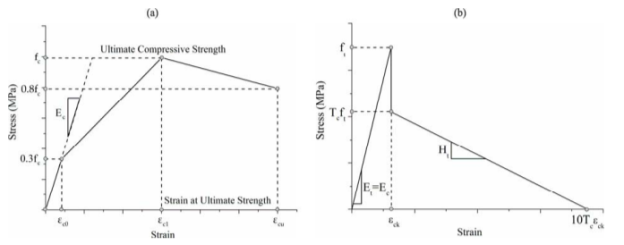
Рис. 1. Соотношение напряжение-деформация для HSC (а) одноосное сжатие, (б) одноосное растяжение
Для бетона были применены шестигранные элементы. Конечный элемент определяется изотропными свойствами материала, восемью узлами с тремя степенями свободы в каждом из них и перемещениями узлов в трехмерной ортогональной локальной системе координат. В каждом конечном элементе деформация и напряжение вычисляются во всех точках численного интегрирования. В состоянии растрескивания и раздавливания матрица жесткости конечного элемента адаптируется к состоянию повреждения. Параметр βt введен для уменьшения передачи сдвига, вызывающей скольжение в плоскости, перпендикулярной поверхности трещины.
Соотношение между напряжением и деформацией бетона с трещинами в одной плоскости описывается следующей матрицей жесткости
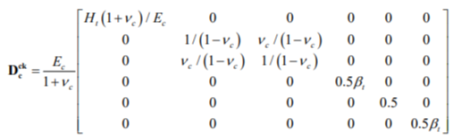
Графическая интерпретация параметра размягчения Ht и множителя Tc для растягивающего напряжения релаксация показана на рисунке 1б. Более подробную информацию можно найти в [2].
Моделирование стали. Упругопластическая модель с линейным упрочнением и таким же соотношением напряжение-деформация для растяжения и сжатия применяется для арматурных стержней, рис. 2.
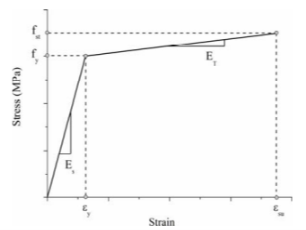
Рис. 2. Соотношение напряжений и деформаций для стальной арматуры
При моделировании стержней был применен пространственный лонжеронный элемент с двумя узлами и тремя степенями свободы в каждом из них. Кроме того, для стальных пластин, расположенных в точках опоры и нагружения, была принята линейно-упругая модель. Шестигранные элементы были применены к моделируемым стальным пластинам. Предполагается идеальное сцепление между материалами. Арматура соединена с узлами бетонной сетки. Таким образом, бетон и арматурная сетка имеют одни и те же узлы, и бетон занимает одни и те же области, захваченные арматурными стержнями.
Численные решения уравнений равновесия. Метод Ньютона-Рафсона представляет собой итерационный процесс решения нелинейных уравнений. Матрица жесткости и вектор восстанавливающих нагрузок рассчитываются на основе вектора перемещения. Матрица жесткости в Методе Ньютона-Рафсона с модификацией адаптивного спуска описывается как сумма двух матриц [5]
K Т t = xK S + (1-x) K T (3)
где: KS — матрица секущей жесткости, K T — матрица касательной жесткости, ξ — параметр адаптивного спуска.
Метод основан на согласовании параметра адаптивного спуска ξ в итерации равновесия. Матрица секущей жесткости генерируется численным методом как эффект нелинейной пластичности, жесткости при больших деформациях, дроблении бетона и релаксации напряжений после растрескивания.
Метод определения длины дуги. В методе определения длины дуги уравнение зависит от параметра нагрузки λ [16]
K i T Δu i = lF α — F nr i (4)
Вектор инкрементального смещения Δui состоит из двух составляющих
Δu i = Δlu i l +Δu ll i (5)
где: Δui / — вектор приращения смещения, вызванный параметром единичной нагрузки, Δui II — вектор приращения смещения в алгоритме Ньютона-Рафсона. Параметр приращения нагрузки Δλ ищется из уравнения дополнительных ограничений, основанного на обеспечении ортогональности. Было обнаружено, что сходимости решений при установке по умолчанию пределов допуска сходимости было трудно достичь из-за нелинейного поведения железобетона. Поэтому пределы допуска на смещение были увеличены до 5 %, чтобы получить сходимость решений.
Численные результаты и обсуждение. Размеры прямоугольных балок, протестированных в [6], были приняты для численных пространственных моделей балок. Размеры, усиление и расположение нагрузки/опоры показаны на рисунке 3.
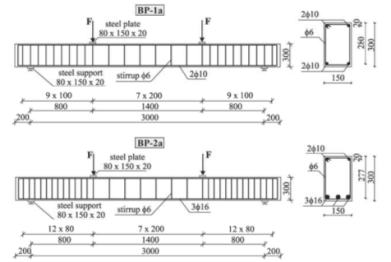
Рис. 3. Размеры балок с усилением и расположением нагрузки/опоры (единица измерения в мм)
Половина балки была смоделирована с учетом продольной симметрии. Стальные пластины на опоре были смоделированы как узловые, передающие усилия на ролики. Допускалось свободное вращение балки в плоскости изгиба. Внешнее усилие также прикладывается через стальную пластину. Предполагалось равномерное распределение усилий в узлах в направлении поперечной оси симметрии стальной пластины.
Влияние модуля упругости и коэффициента передачи сдвига на кривые зависимости нагрузки от прогиба. Прочность на сжатие необходима для определения других параметров нелинейной модели. Расчеты модельной балки, изготовленной из бетона с прочностью на сжатие 81,2 МПа, были выполнены для оценки влияния модуля упругости (Ec) и коэффициента передачи сдвига для открытой трещины (βt) на кривые зависимости нагрузки от прогиба. Различные соотношения между прочностью на сжатие и значения модуля упругости для высокопрочного бетона приведены в таблице 1. Можно отметить, что рассчитанные значения модуля упругости имеют большой разброс результатов.
Таблица 1
Уравнения для определения модуля упругости высокопрочного бетона (литературные данные)
|
Уравнения |
Ec (МПа) для fc = 81,2 МПа |
|
|
CEB-FIB |
Ec=
|
44681 |
|
CAN A23.3-M90 |
Ec=
|
45056 |
|
ACI 363 |
Ec=
|
36817 |
|
Проф. Кикидзаки [17] |
Ec=
|
32890 |
|
Проыф. Невилл [17] |
Ec=
|
42649 |
При анализе зависимости нагрузки от прогиба в середине пролета для балки, полученной в ходе экспериментальных испытаний и в МКЭ анализ для различных значений модуля упругости было обнаружено, что предложение по расчету модуля упругости в соответствии с ACI 363 дает кривую наилучшего соответствия. Численные расчеты анализа влияния коэффициента передачи сдвига для открытой трещины были выполнены с использованием метода Ньютона Рафсона с адаптивным спуском. Для коэффициента βt, равного 0,5, были получены результаты, аналогичные экспериментальным данным.
Выводы
Изменяемый шаг нагрузки и правильная настройка параметров обеспечивают более быстрое численное вычисление и, кроме того, гарантируют точные решения. Кроме того, стальные пластины, размещенные на опоре и в точке нагрузки, очень важны для отображения граничных условий во время экспериментальных испытаний. В этом исследовании полезность метода была проверена на пространственных моделях армированных высокопрочных бетонных балок. Результаты, полученные в результате численного и экспериментального анализа, сравниваются друг с другом. Видно, что поведение конечного элемента при отказе указывает на хорошее соответствие с поведением при тестировании.
Литература:
- V. Afroughsabet, T. and Ozbakkaloglu, “Mechanical and durability properties of high-strength concrete containing steel and polypropylene fibers,” Constr. Build. Mater., vol. 94, pp. 73–82, 2015.
- S. Teng, T. Y. D. Lim and B. S. Divsholi, “Durability and mechanical properties of high strength concrete incorporating ultra-fine ground granulated blast-furnace slag,” Constr. Build. Mater., vol. 40, pp. 875–881, 2013.
- M. Mazloom, A. A. Ramezanianpour, and J. J. Brooks, “Effect of silica fume on mechanical properties of high-strength concrete,” Cem. Concr. Compos., vol. 26, pp. 347–357, 2004.
- M. E. Kamińska, “High-strength concrete and steel interaction in RC members,” Cem. Concr. Compos., vol. 24, pp. 281–295, 2002.
- M. A. Rashid, and M. A. Mansur, “Reinforced high-strength concrete beams in flexure,” ACI Struct. J., vol. 102, pp. 462–471, 2005.
- D. M Özcan., A. Bayraktar, A. Şahin, T. Haktanir, and T. Türker, “Experimental and finite element analysis on the steel fiber-reinforced concrete (SFRC) beams ultimate behavior,” Constr. Build. Mater., vol. 23, pp. 1064–1077, 2009.
- M. Słowik, and P. Smarzewski, “Study of the scale effect on diagonal crack propagation in concrete beams,” Comp. Mater. Sci., vol. 64, pp. 216–220, 2012.
- A. Stolarski, “Dynamic strength criterion for concrete,” J. Eng. Mech.-ASCE, vol. 130, pp. 1428–1435, 2004.
- A. M. Neville, “Properties of Concrete,” 4th ed., Longman, England, p. 868, 2000.