Параметризация в задаче распознавания диктора по речевому образцу заключается в выделении наиболее информативных параметров речи и получение компактного описания речевого сигнала. Размерность пространства параметров измеряется десятками. Так, число кепстральных коэффициентов может варьироваться от 10 до 30. Обычно к ним добавляются первые и вторые разности по времени (дельтапараметры), так что размерность пространства признаков для каждого кадра находится в диапазоне от 30 до 90. В общем случае это число должно быть умножено на количество кадров в речевом высказывании, что приводит к размерностям в сотни параметров. Для аппроксимации параметров прибегают к кластерному анализу [1,с.52].
Кластерный анализ — задача разбиение заданной выборки объектов на подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались.
Существует множество методов кластеризации. Из методов вероятностного подхода наиболее используемыми являются метод k-means, k-medians, EM-алгоритм. Из методов на основе искусственного интеллекта часто применяют метод нейронных сетей Кохонена. [2,с. 8]
Наиболее надежным способом идентификации диктора в текстонезависимых системах является векторное квантование [3, с.124], основанное на кластеризации векторов признаков. Множество обучающих векторов преобразуется в множество кодовых слов (векторов), называемое кодовой книгой. Происходит сокращение избыточно большой исходной выборки обучающих параметров путем замены векторов в кластере на наиболее типичного представителя в каждом кластере. Обычно размер кодовой книги выбирается равным 256 или 512. Таким образом, метод векторного квантования применяется для конструирования аппроксимирующих акустических прототипов, используемых в качестве акустических моделей-эталонов.
При идентификации говорящего по поступающему речевому сообщению распределение кластеров оказывается похожим на эталонное для зарегистрированного пользователя, или отличающееся для злоумышленника. Классификация производится вычислением меры близости (сходства) пробных данных и уже известных, которая выражается расстоянием от вектора признаков пробного сигнала до вектора признаков уже классифицированного. В качестве меры близости для числовых атрибутов очень часто используется евклидово расстояние, которое представляет собой геометрическое расстояние в многомерном пространстве:
Распространённым методом построения кодовой книги является алгоритм k-средних.
Метод оперирует таким понятием как центроид. Центроид — центр масс кластера, координаты которого рассчитываются как среднее значений координат объектов кластера в пространстве данных.
Алгоритм k-средних разбивает исходное множество на k кластеров, где k — предварительно заданное число. Для этого сначала значения средних инициализируются некоторыми векторами из исходного множества. Затем на каждой итерации алгоритма происходит распределение векторов в ближайшие к ним кластеры (для этого вычисляется расстояние между вектором и текущими значениями средних) и перерасчёт среднего в каждом кластере. Для каждого полученного разбиения рассчитывается некоторая оценочная функция D — средняя ошибка квантования, distortion (англ. искажение) [4,с.13]:
Где N-количество обучающих векторов;
![]() -вектор
среднего;
-вектор
среднего;
![]() -
обучающий вектор, принадлежащий кластеру с центроидом
-
обучающий вектор, принадлежащий кластеру с центроидом
![]() .
.
Алгоритм k-means стремится минимизировать суммарное отклонение точек в кластере от центров кластеров.
Процесс вычисления средних и перераспределения объектов заканчивается тогда, когда кластерные центры стабилизировались, т. е. все наблюдения принадлежат кластеру, которому принадлежали до текущей итерации. Минимизация оценочной функции позволяет сделать результирующие кластеры настолько компактными и раздельными, насколько это возможно. Такое разбиение параметрического пространства является диктороспецифическим.
Полученные значения средних являются кодовыми векторами, используемыми для построения шаблона — кодовой книги.
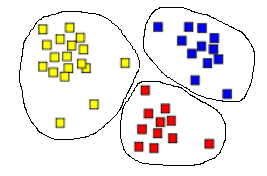
Разбиение параметрического пространства на 3 кластера методом k-means показано на рисунке 1.
Рис. 1.Результат кластеризации алгоритмом k-means (k=3)
Метод k-means хорошо работает, когда кластеры представляют собой значительно разделённые между собой компактные области. Он эффективен для обработки больших объёмов данных, однако не применим для обнаружения кластеров невыпуклой формы или сильно различающегося размера.
Литература:
X.Huang, A.Acero, H.Hon. Spoken Language Processing: A guide to theory, algorithm, and system development. Prentice Hall, 2001.
Lawrence R. Rabiner, Ronald W. Schafer Introduction to Digital Speech Processing, 2007
Аграновский А. В., Леднов Д. А. Теоретические аспекты алгоритмов обработки и классификации речевых сигналов Москва: Изд-во «Радио и связь», 2004. 164 с.
ETSI ES 202 050 V1.1.5 (2007–01) ETSI Standard Speech Processing, Transmission and Quality Aspects (STQ); Distributed speech recognition; Advanced front-end feature extraction algorithm; Compression algorithms