Исследование напряженно-деформированного состояния гнутых карнизных узлов рам

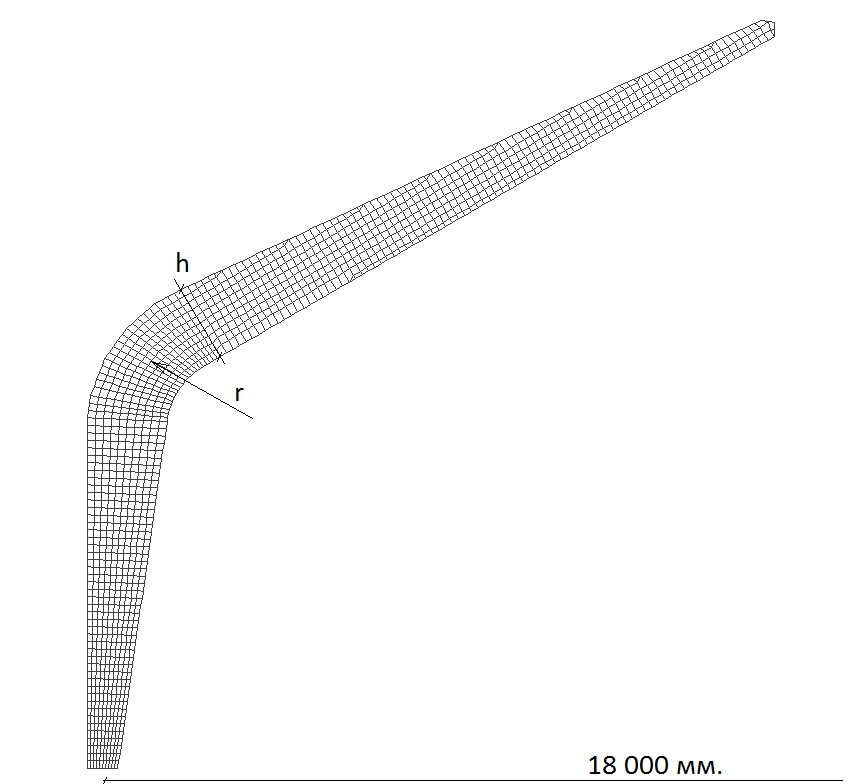
В настоящее время потребность в деревянных строительных конструкциях возрастает ежегодно. Значит, выбор наиболее оптимальных и экономически выгодных конструктивных схем является наиболее перспективных областей исследований в области деревянных конструкций. В настоящей статье будут рассматриваться гнуто карнизные узлы деревянных рам. Неблагоприятные условия в карнизном узле возникают в раме с трехшарнирным закреплением, поэтому для дальнейшего исследования выберем ее.

Методика построения конечно элементной модели

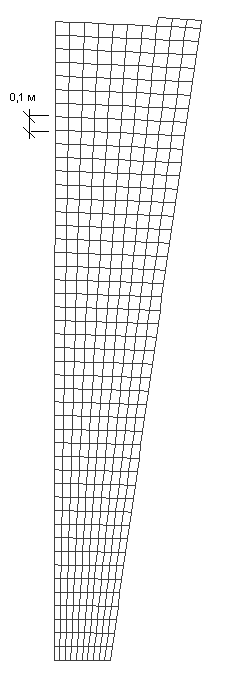
Схема была разбита вручную МКЭ в виде пластин. Для достижения более лучшей картины напряжений разработана сетка конечных элементов с шагом 0.1 метр. Конструкции гнутого узла, ригеля и стойки разрабатывались отдельно друг от друга.

Последовательность разбивки гнутого узла

1. По внешнему и внутреннему контуру радиуса узла были размещены точки с шагом 0.1 м (рис.1)

2. От точек внешнего контура рамы проводились прямые к точке построения радиуса (АО, ВО, СО и т. д.) и на пересечении этих элементов и элементов внутреннего контура отмечались точки пересечения(1,2,3,4, и т. д.).

3. В зависимости от высоты сечения, элемент по высоте разбивался на определенное количество точек с шагом 0.1 м.

4. На полученном поле точек с помощью функции «добавление пластины» строились элементы по четырем точкам.

Рис. 1. Последовательность моделирования узла

Площадь элементов уменьшается к точке построения радиуса.

Такая схема расположения пластин в пространстве была разработана и принята вследствие более точных результатов, правильной ориентации элементов, отсутствия элементов и нежелательных сопряжений дающих нечеткую картину исследуемых результатов.

Рис. 2. а) Ручная разбивка сетки б) Автоматическая разбивкаSCAD.

Последовательность разбивки ригеля:

1. После построения узла, в зависимости от количества горизонтальных точек верха ригеля, на такое же разбивается нижняя.

2. С помощью функции «задание контура» обозначается контур через четыре точки, из них две ближайшие верхние и соответствующие им нижние.

3. Производится разбивка контура на пластины. Задается шаг разбивки 0.1 м. Действие повторяется несколько раз.

Таким образом избегается перепад напряжений, появление нежелательных сопряжений и элементов других конфигураций. Улучшается эстетический вид.

Рис. 3. Последовательность моделирования ригеля

Граничные условия

Для реализации расчетной схемы в М. К. Э. необходимо было правильно задать условия, что становится проблематичным, так как рассчитываемая модель становится не стержневой, а плоской. В связи с этим был разработан шарнирный узел для пластинчатого конечного элемента.

Последовательность разработки:

1. От середины нижней части рамы была удаленна точка на 0,3 м. В ней были запрещены перемещения в направлениях Х YZ.

2. В крайней точке справа запрещены перемещения в направлении Х

3. с помощью команды «объединение перемещений» перемещения по направлениям Х YZUxUzUy в нижних точках рамы, и точки удаленной от рамы совмещаются, как показано на Рис.4

4. В верхней части моделируется шарнир, задаются ограничения в серединной точке по направлениям Х YUxUy. Точка показана на Рис.5

Рис. 4. Шарнирное закрепление рамы в нижней части

Рис. 5 .Шарнирное закрепление рамы в верхней части.

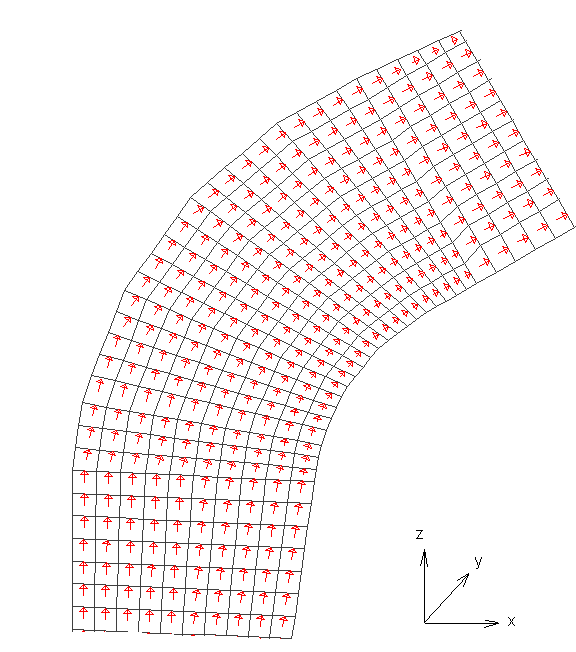
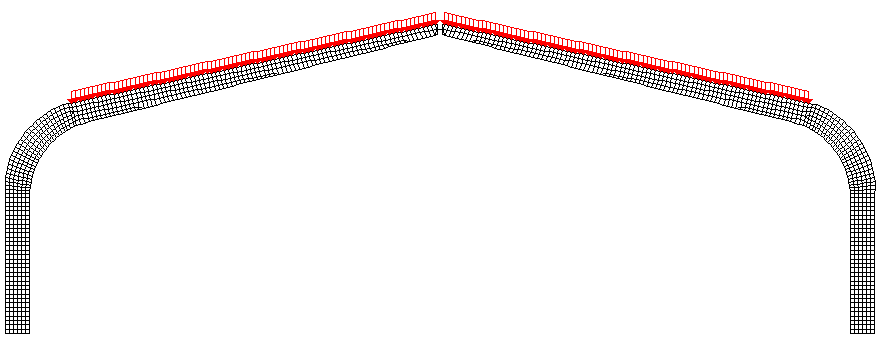
Все внутренние напряжения в каждом пластинчатом конечном элементе были выровнены по направлению вдоль волокон древесины, что предоставляет реальную картину происходящих процессов в исследуемой раме.

Рис. 6. Схема выдачи внутренних напряжений

Рис. 7 Общий вид рамы разбитой на конечные элементы

Исходные данные для расчетов

Параметры образцов, подвергаемых теоретическому расчету, назначались исходя из поставленных целей исследования. Изменчивыми параметрами являлись:

• радиус гнутья рамы, r

• высота сечения рамы h.

Не изменяемыми параметрами являлись:

• ширина пролета рамы 18 м;

• толщина балок -δ

Расчет производился при действии на образец силы равной q=1 т/м.

Было принято несколько видов образцов рамы, размеры которых описаны в табл.1.

Таблица 1

Основные характеристики образцов

Результаты расчета исследуемых рам представленны в научно-исследовательской работе Сащенко Е. О. [2]

Сравнение результатов с экспериментальными исследованиями

Цель сравнения данных

Целью исследований является подтвердить целесообразность выбора модели построенной рамы и точность получаемых результатов. Для этого было принято использовать на ранее проведенные экспериментальные исследования напряженно-деформированного состояния клееных рам и выявление их несущей способности при статических нагрузках, описанных в диссертации Табунова С. Ю. [1]

Разработка и моделирование проведенного эксперимента

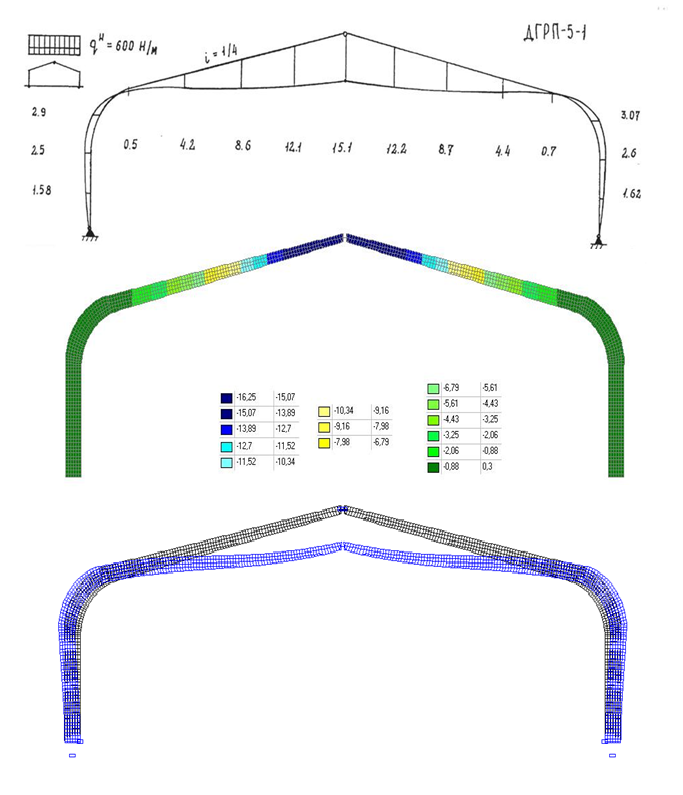
В программном комплексе SCAD были смоделированы две рамы с помощью принятой методике разбивки на конечные элементы, они же для экспериментальных исследований были изготовлены в диссертации. Рамы серии — пролетом 5 м моделировались по геометрической схеме с уклоном ригеля, принятым в типовых проектах (1:4), и с уклоном, принятым на основе предварительных технико-экономических расчетов. Размеры поперечных сечений назначались из расчета рам без учета дополнительного момента от нормальной силы. Расчетная нагрузка определялась из условия прочности по краевым напряжениям в карнизном узле и на скалывание у опоры. Основные размеры экспериментальной рамы [1] приведены в таблица 1. Схема испытательной установки и назначение модели рамы приведены на рис. 8, 9. Результаты эксперимента приведены на рис.10 и 11.

Рис. 8. Схема испытательной установки и расстановки приборов в раме [4]. П1-Прогибомеры типа 6ПАО; T — тензометры Н. Н. Аистова; индикаторы часового типа; 5–5 — сечения (оснащенные тензорезисторами)

Рис. 9. Схема расчетной модели рамы построенной в Программном комплексе SCAD 11.3

Анализ результатов

Рис. 10. Экспериментальные кривые перемещений осей рам серии ДГРП-5–1- при нормативной нагрузке: а) симметричная по данным Табунова С. Ю. [4]; б) по расчету в SCAD 11.3

Анализ результатов

Анализируя полученные результаты, следует отметить, что нормальные (тангенциальные) напряжения меняют свою форму от линейной в прямолинейных и переходных участках до близкой к гиперболической (с незначительным искажением в виде вогнутости вблизи растянутой кромки) в зоне биссектрисы. Такой характер отклонения в растянутой зоне объясняется влиянием анизотропии. Распределение касательных напряжений так же имеет специфический характер. Если в прямолинейном участке (сечение 9) эпюра имеет симметричную параболическую форму, то в переходном участке очертание эпюры изменяется, появляется асимметричность с местным увеличением вблизи растянутых кромок. Максимальные значения касательных напряжений смещаются в сторону сжатой зоны.

Выводы

1. Практика отечественного и зарубежного строительства показала экономическую и техническую целесообразность применения клееных деревянных рам в качестве несущего каркаса в зданиях общественного, спортивного, промышленного и других типов зданий. Рамы имеют существенных преимуществ: транспортабельность, легкость, надежность, эстетичность, экологичность и др.

2. Конструктивные расчеты показали, что наряду с трех шарнирными клееными рамами целесообразно и экономически выгодно применять одношарнирные статически неопределимые клееные рамы. Такие рамы более технологичны в изготовлении и экономически выгодны по расходу древесины, поскольку обладают меньшими расчетными усилиями при прочих одинаковых условиях чем трехшарнирные.

3. Разработанная методика построения расчетной модели деревянной гнутоклееной рамы с помощью прямоугольных конечных элементов в программном комплексе SСAD дает более достоверный и точный результат исследуемых параметров.

4. Полученные картины напряженно деформированного состояния криволинейной части гнутоклееной деревянной рам, позволяющие оценить действительную работу рам и назначить параметры сечения, с учетом этих факторов.

5. Проведенные теоретическое исследования показали зависимость уровня напряженного состояния гнутой части рамы от таких параметров, как радиус кривизны,высоты поперечного сечения относительно радиуса кривизны (r/h), толщины склеенных досок по отношению к радиусу (δ/r)получены зависимости максимальных напряжений от исследуемых параметров рамы.

6. Полученные результаты исследований показали хорошую достоверность путем сравнения их с экспериментальными данными, приводимыми в диссертационной работе Табунова С. Ю. Расхождения при сравнительном анализе составили не более 4–8 %,что указывает на возможность исследования данной методики расчета в практическом проектировании.

Литература:

1. Расчет и выбор оптимальных параметров РАМ с прямолинейным ригелем и гнутоклееными стойками для сельскохозяйственных зданий: диссертация... кандидата технических наук Табунова С. Ю.: 05.23.01 61 85–5/236 Ленинград, 1984

2. «Оптимизация параметров гнутоклееных рам и совершенствование методов их расчета» Сащенко Е. О., ПГУАС, Пенза, 2010 г