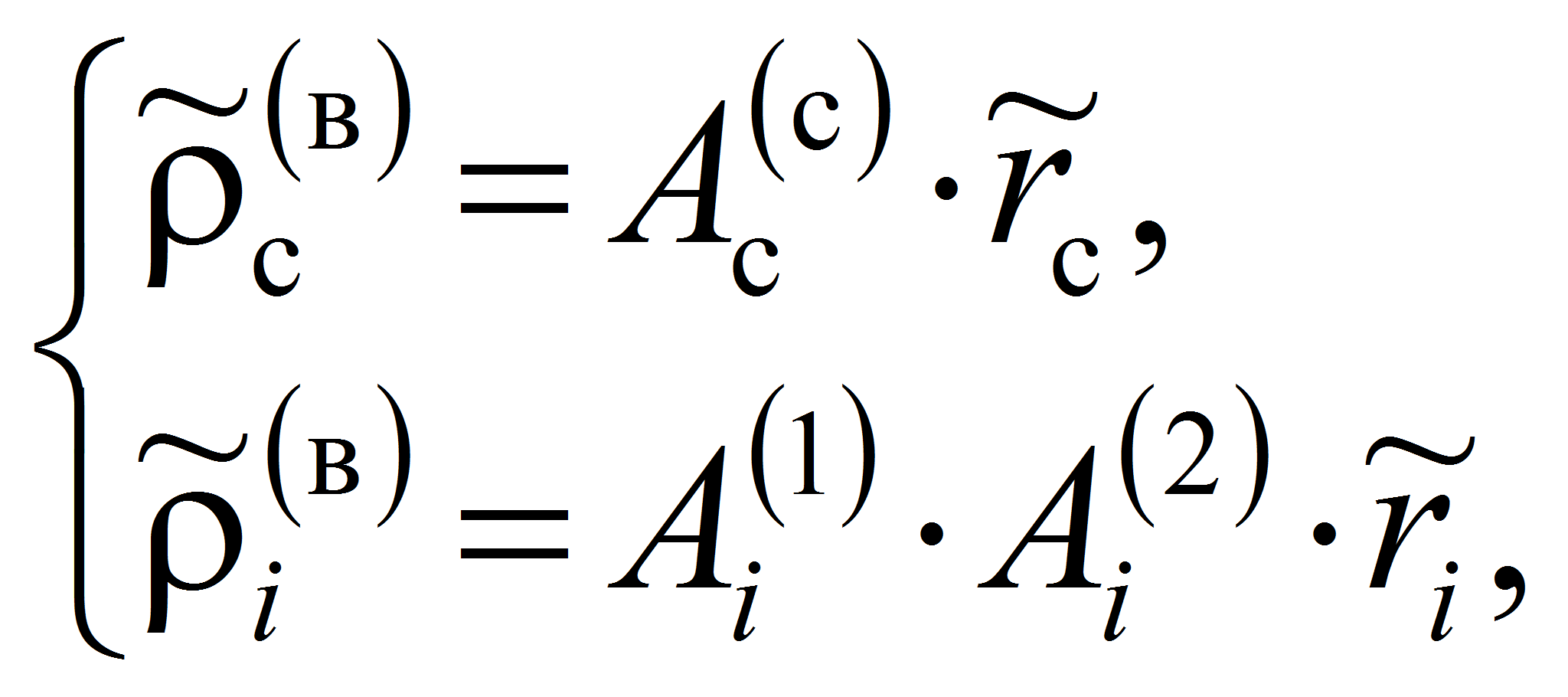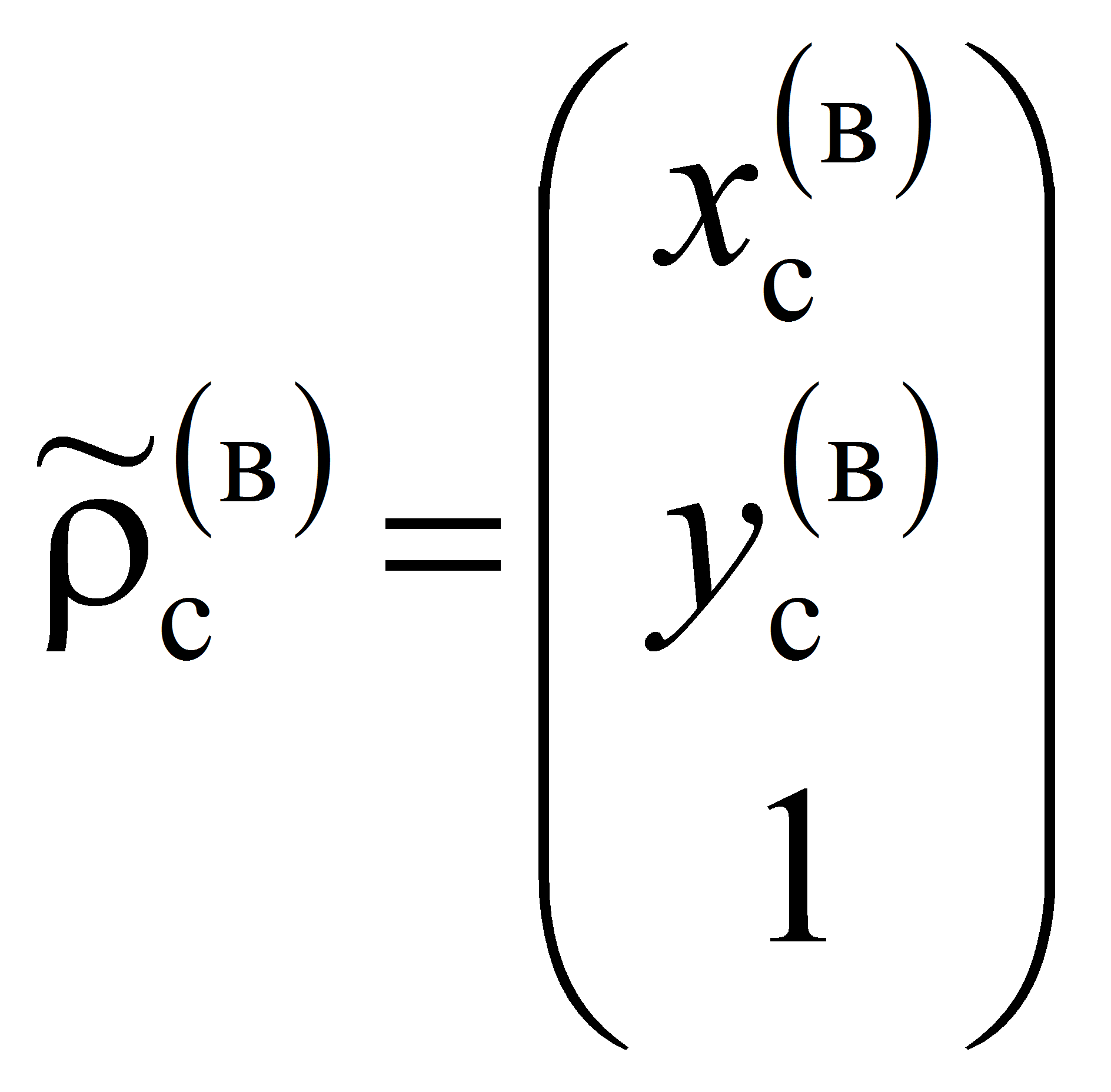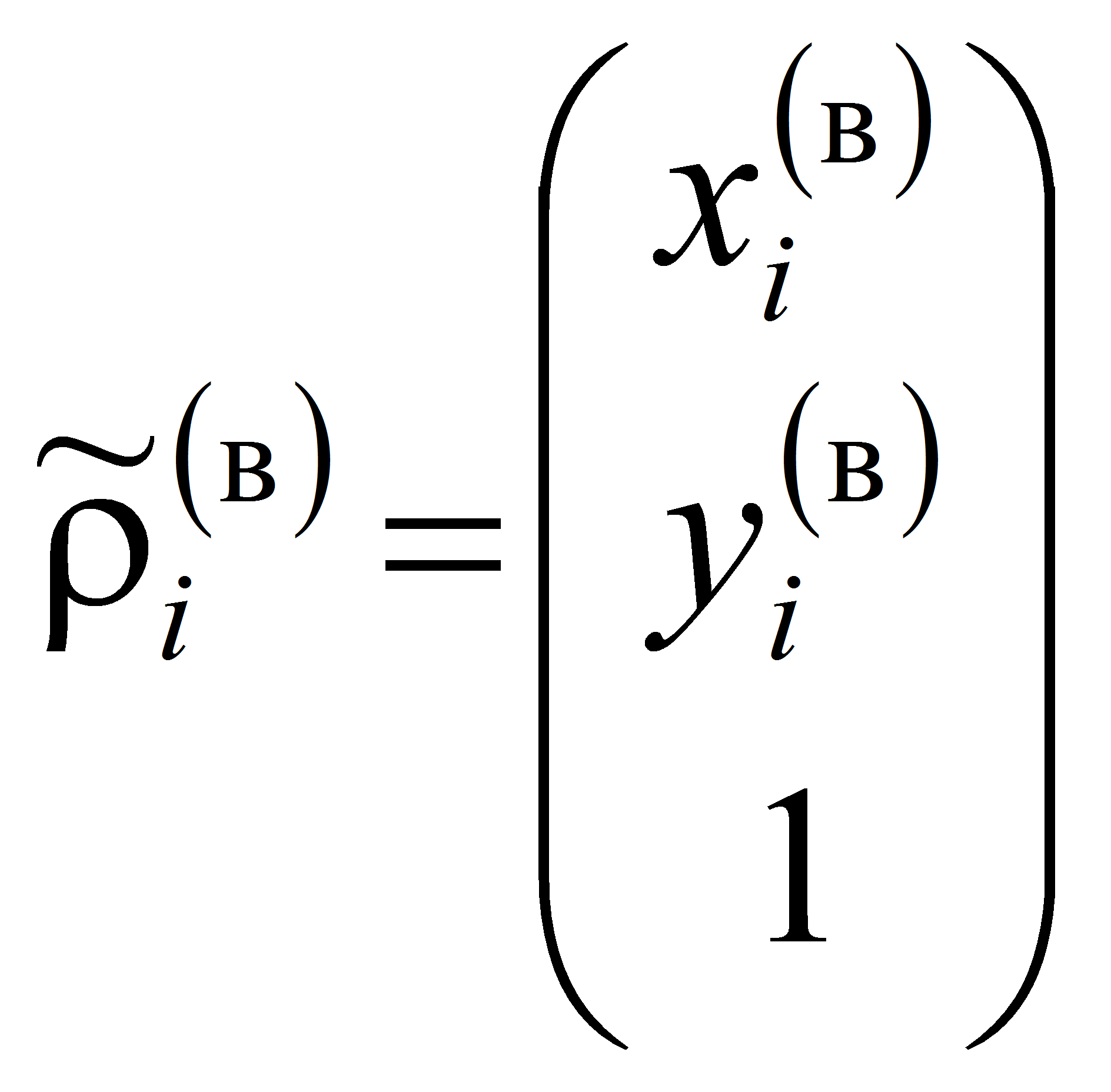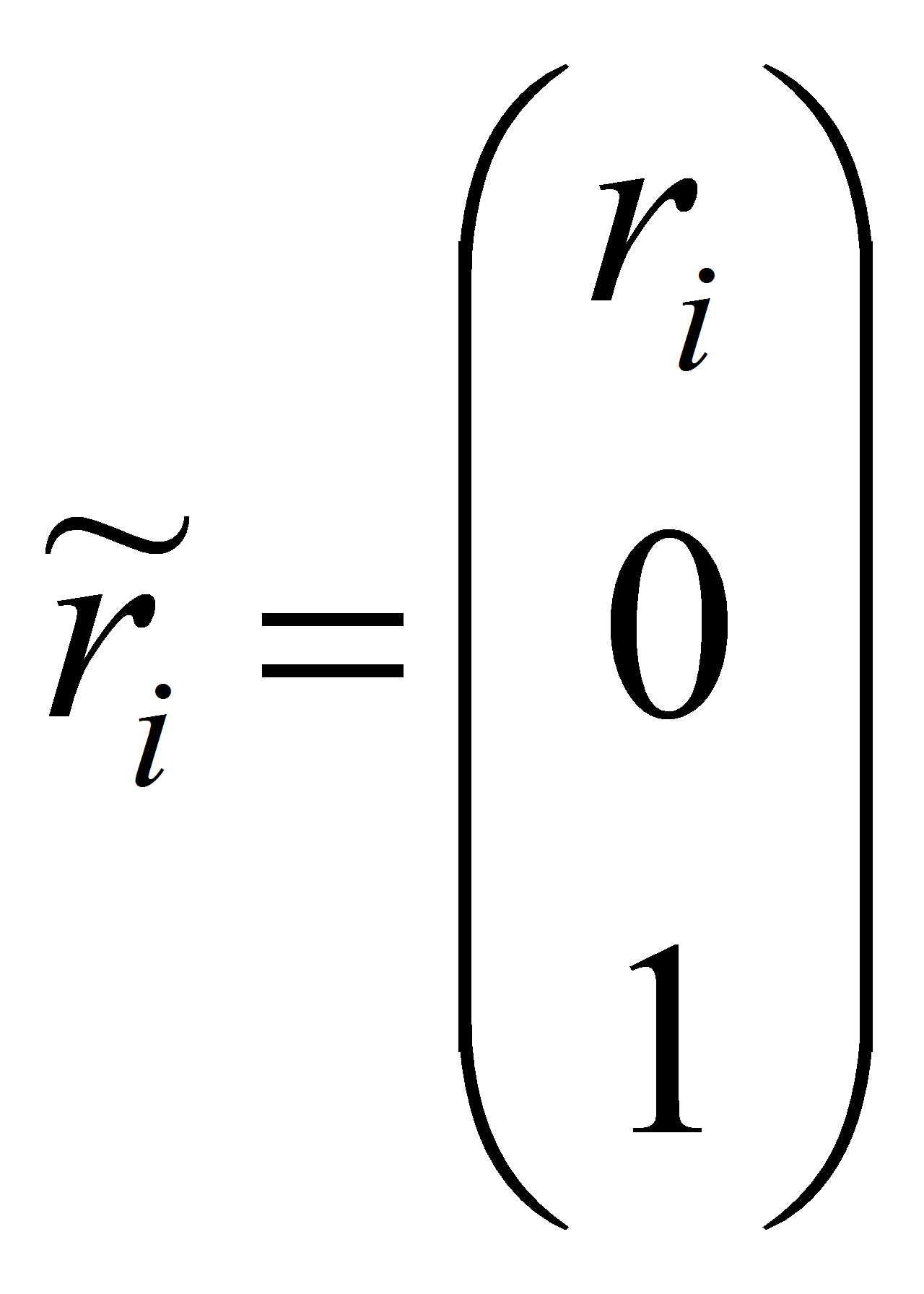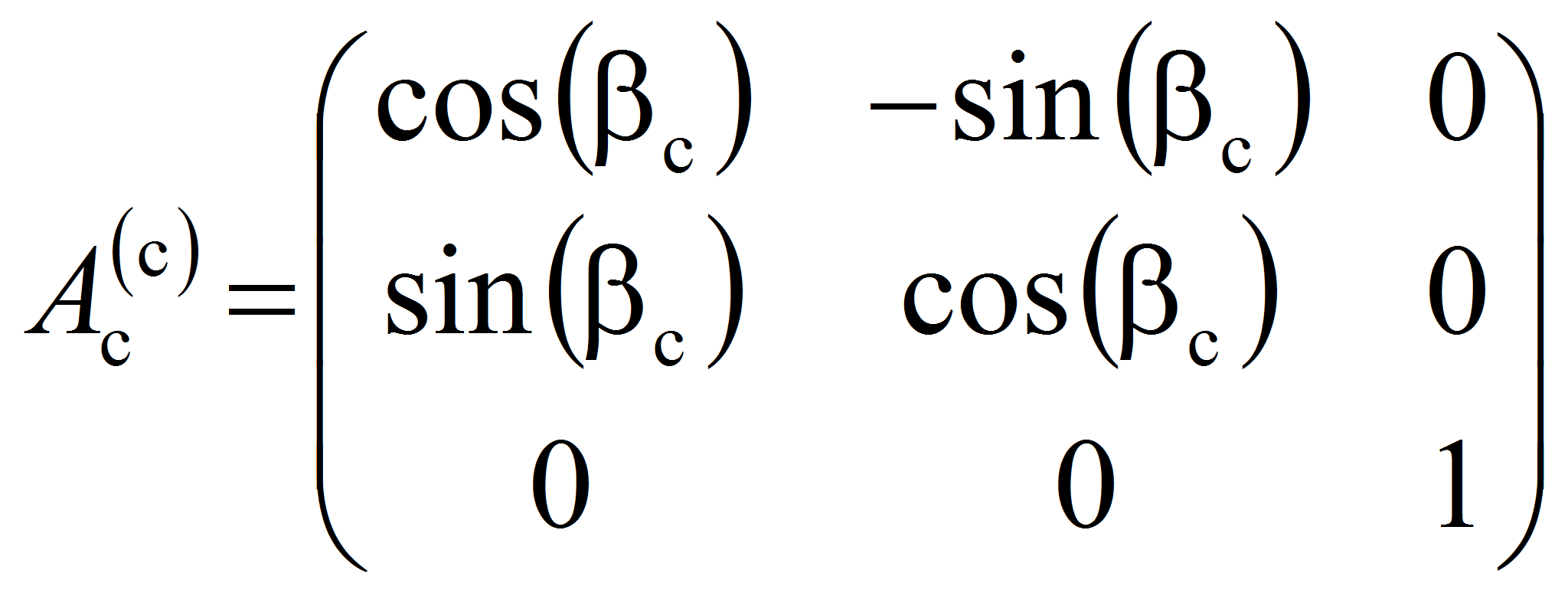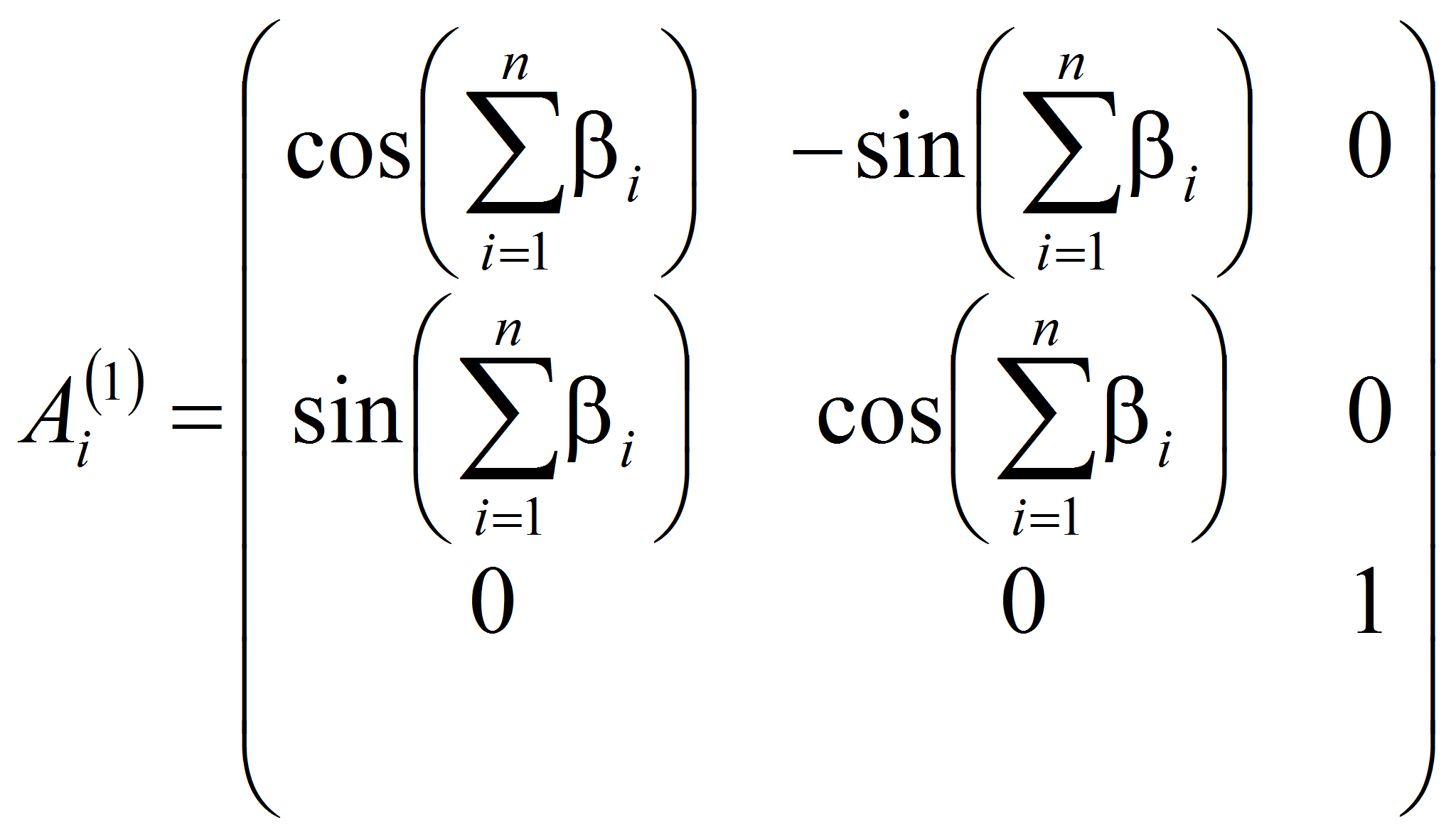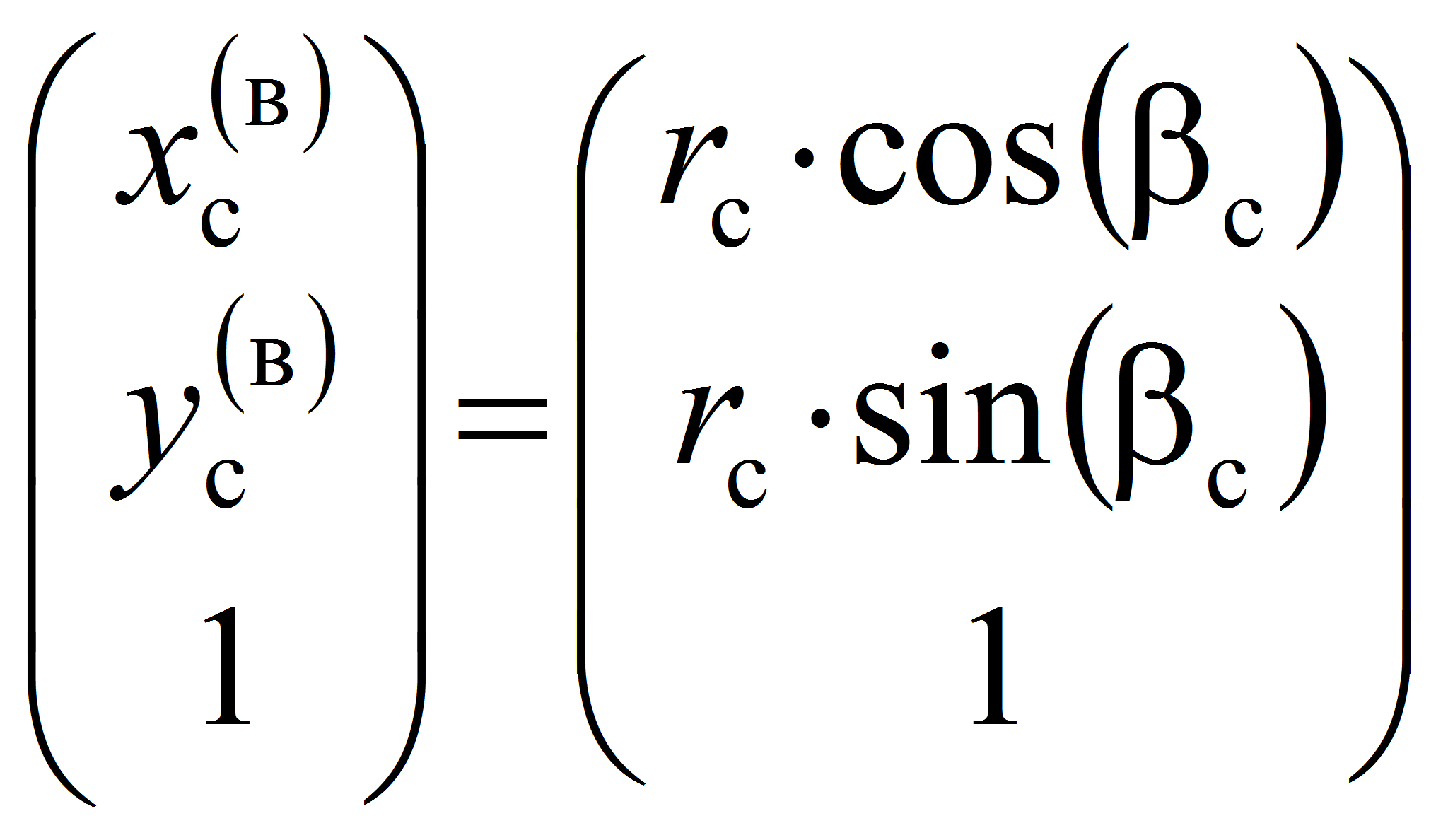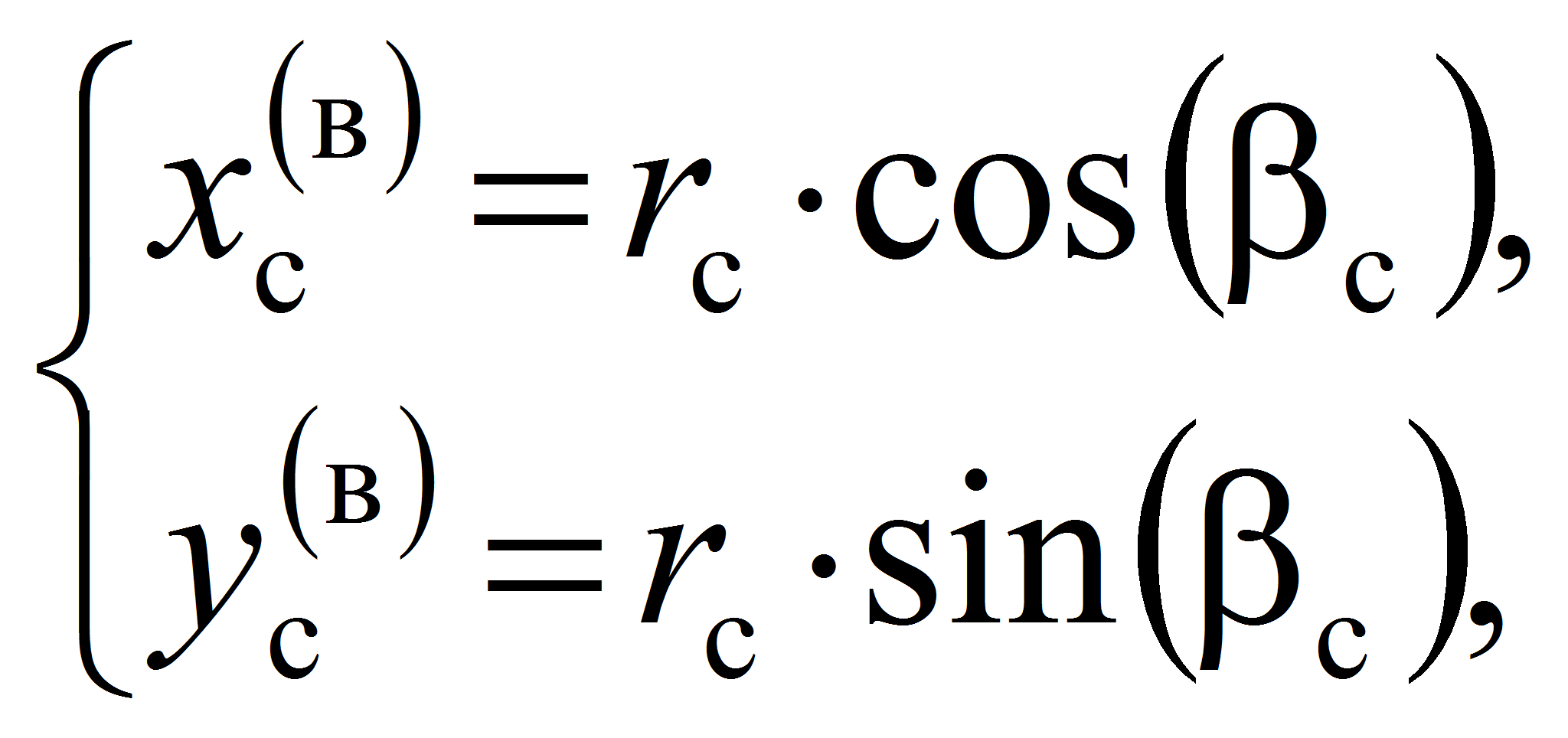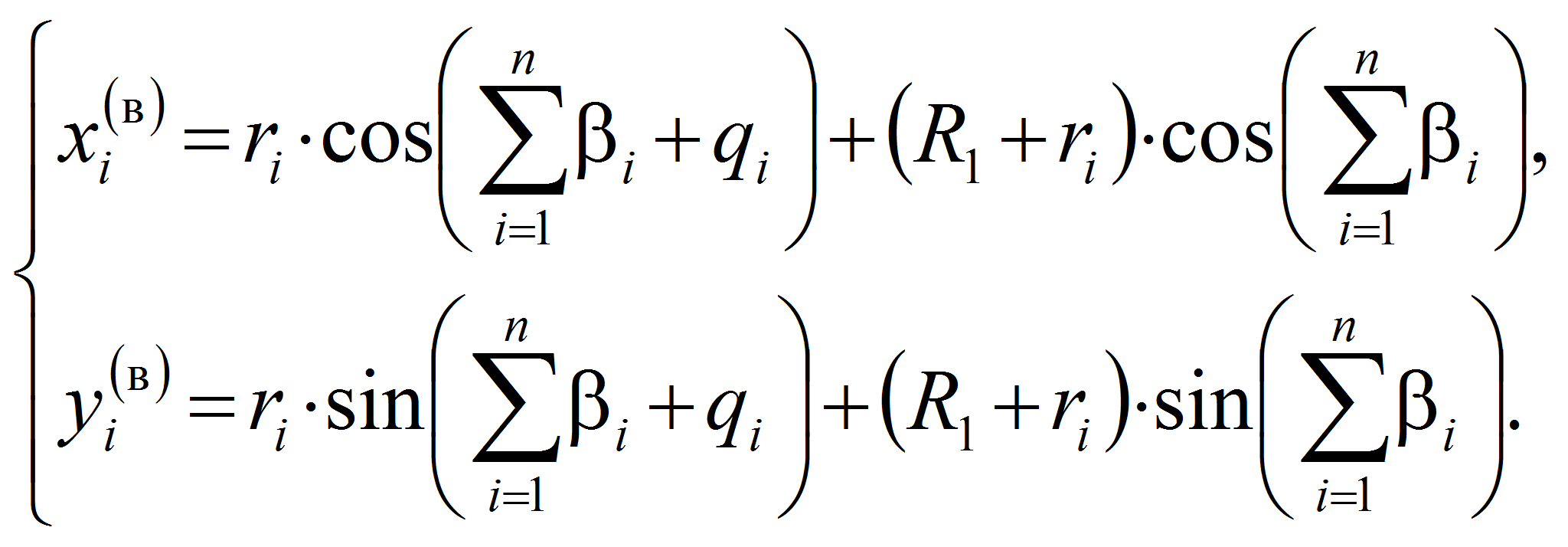Рассматривается общий случай решения задачи о положении звеньев механизма-прототипа эксцентрикового механизма качения (ЭМК) по средствам формирования математической модели.
Ключевые слова: механизм-прототип, эксцентриковый механизм качения, тела качения, сепаратор, математическая модель, декартовая система координат, столбцовая матрица, система параметрических уравнений.
Реализация заданного закона движения выходного звена исполнительного механизма технологического оборудования, разработанного на базе эксцентрикового механизма качения (ЭМК) определяется точностью положений его звеньев в пространстве или на плоскости в определенные моменты времени. Решение задачи о положениях звеньев ЭМК в явном виде возможно при помощи математической модели составленной для механизмов данного вида с учетом особенностей строения их структуры [1, 2].
Эксцентриковый механизм качения разработан на базе механизма-прототипа являющегося разновидностью механизмов с замкнутой системой тел качения. Для ЭМК характерно наличие смещения центров дорожек качения наружного и внутреннего колец относительно друг от друга на величину эксцентриситета, что обеспечивается использованием тел качения с диаметрами разной величины [3]. В настоящее время коллективом авторов проводятся теоретические [3, 4] и экспериментальные [5, 6] исследования геометрических и кинематических параметров механизмов технологического оборудования разработанного на базе, как ЭМК, так и механизма-прототипа [7].
Структура механизма-прототипа эксцентрикового механизма качения содержит сепаратор (водило) и замкнутую систему тел качения с диаметрами одинаковой величины, что обеспечивает совпадение центров дорожек качения наружного и внутреннего колец. Решение задачи о положениях звеньев механизма-прототипа ЭМК в явном виде так же при помощи математической модели составленной для механизмов данного вида с учетом особенностей строения их структуры.
Применим элементы теории матриц [8] для описания математической модели механизма-прототипа ЭМК с сепаратором (водило) при ведущем внутреннем кольце. Данный метод позволит в компактной форме получить совокупность выражений описывающих положения звеньев относительно систем координат каждого звена. При выборе систем координат звеньев необходимо, чтобы эти системы могли быть совмещены друг с другом посредством одного поворота и одного перемещения.
Для получения функций
положения звеньев механизма-прототипа
ЭМК составим расчетную модель (рис. 1) и примем следующие
исходные условия и обозначения: ведущим звеном является
внутреннее кольцо; Rв,
Rн,
Ов
и Oн —
радиусы и геометрический центр дорожек качения внутреннего
и наружного колец; r0,
r1,
ri
и x0,
y0,
x1,
y1,
xi,
yi —
радиусы и координаты центров тел качения; системы координат
звеньев — левые; X(в)O(в)Y(в) —
неподвижная декартовая система координат с центром в точке
O(в);
![]() —
декартовая система координат сепаратора (водило) с началом
в точке O(в)
и отличающаяся от других систем на угловую координату c;
—
декартовая система координат сепаратора (водило) с началом
в точке O(в)
и отличающаяся от других систем на угловую координату c;
![]() ,
,
![]() ,…,
,…,![]() —
декартовые системы координат с общим началом в точке O(в),
отличающиеся друг от друга на угловые координаты i;
—
декартовые системы координат с общим началом в точке O(в),
отличающиеся друг от друга на угловые координаты i;
![]() ,
,
![]() ,…,
,…,![]() —
декартовые системы координат с началом в центрах тел
качения и отличающиеся друг от друга на угловую координату qi.
Начала отсчета всех систем координат связанны с геометрическими
центрами звеньев механизма-прототипа ЭМК и лежат в точках
расположенных на осях их вращения, а ось Z каждой
системы координат совпадает этими осями. Во всех системах координат
i=1,2,…,z;
где z —
число тел качения содержащихся в структуре механизма.
—
декартовые системы координат с началом в центрах тел
качения и отличающиеся друг от друга на угловую координату qi.
Начала отсчета всех систем координат связанны с геометрическими
центрами звеньев механизма-прототипа ЭМК и лежат в точках
расположенных на осях их вращения, а ось Z каждой
системы координат совпадает этими осями. Во всех системах координат
i=1,2,…,z;
где z —
число тел качения содержащихся в структуре механизма.
Положения точек Cc,
C0
и Ci,
лежащих на рабочих поверхностях звеньям механизма-прототипа,
относительно выбранных систем координат, описываются положениями
векторов
![]() и характеризуются проекциями на координатные оси (рис 1).
Переход от одной системы координат к другой осуществим при
помощи формул преобразования координат, описываемых матрицами
третьего порядка, т. е. матрицами вращения (поворота)
и перемещения (сдвига) [2, 8].
и характеризуются проекциями на координатные оси (рис 1).
Переход от одной системы координат к другой осуществим при
помощи формул преобразования координат, описываемых матрицами
третьего порядка, т. е. матрицами вращения (поворота)
и перемещения (сдвига) [2, 8].
Выполняя поворот системы
координат
![]() вокруг оси Zc на угол c
таким образом, чтобы ось координат Xc
располагалась параллельно оси X0,
осуществляем переход системы координат сепаратора (водило)
вокруг оси Zc на угол c
таким образом, чтобы ось координат Xc
располагалась параллельно оси X0,
осуществляем переход системы координат сепаратора (водило)
![]() в неподвижную систему координат X(в)O(в)Y(в)
(рис. 1). В результате реализации данных элементарных действий
получаем матрицу вращения (поворота).
в неподвижную систему координат X(в)O(в)Y(в)
(рис. 1). В результате реализации данных элементарных действий
получаем матрицу вращения (поворота).
Для перехода систем
координат
![]() и
и
![]() в неподвижную систему координат X(в)O(в)Y(в)
осуществляем поворот систем координат вокруг оси Zi
соответственно на углы
в неподвижную систему координат X(в)O(в)Y(в)
осуществляем поворот систем координат вокруг оси Zi
соответственно на углы
![]() и qi
таким образом, чтобы оси координат
и qi
таким образом, чтобы оси координат
![]() и
и
![]() располагались параллельно оси
располагались параллельно оси
![]() (рис. 1). В результате выполнения элементарных действий получаем
две матрицы вращения (поворота). Дополнительно для системы
(рис. 1). В результате выполнения элементарных действий получаем
две матрицы вращения (поворота). Дополнительно для системы
![]() выполняем перемещение вдоль оси
выполняем перемещение вдоль оси
![]() на величину
на величину
![]() до совпадения начала отсчета преобразуемых систем, что позволяет
сформировать матрицу перемещения (сдвига).
до совпадения начала отсчета преобразуемых систем, что позволяет
сформировать матрицу перемещения (сдвига).
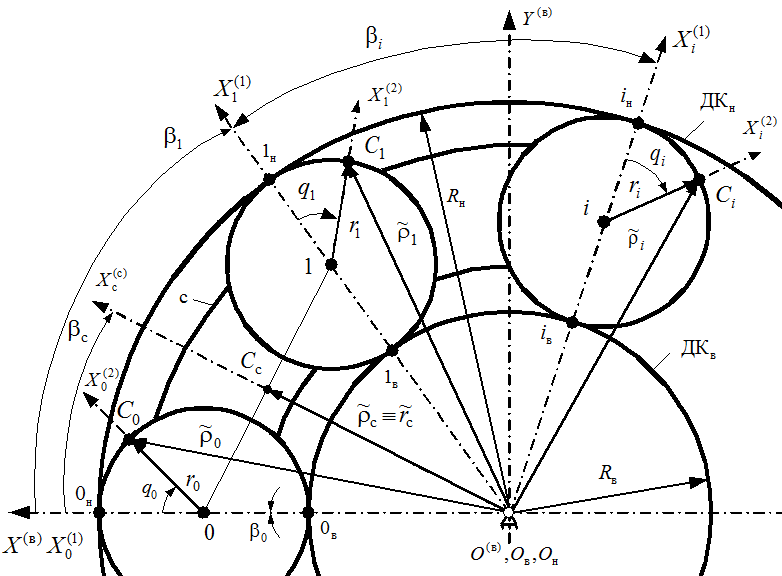
- Рис. 1. Расчетная модель механизма-прототипа ЭМК с сепаратором (водило) при ведущем внутреннем кольце
Положения
точек Cc
и Ci
принадлежащих сепаратору (водило) и i-ому
телу качения содержащихся в структуре механизма-прототипа ЭМК
относительно неподвижной системы координат X(в)O(в)Y(в)
определяются соответственно векторами
![]() и
и
![]() ,
которые в матричной форме имеют вид
,
которые в матричной форме имеют вид
где
![]() ,
,
![]() ,
,
![]() и
и
![]() —
столбцовые матрицы,
—
столбцовые матрицы,
![]() и
и
![]() —
матрицы вращения (поворота),
—
матрицы вращения (поворота),
![]() —
матрица вращения и перемещения (сдвига).
—
матрица вращения и перемещения (сдвига).
Верхний индекс параметров системы (1), соответствует обозначению системы координат, относительно которой определяется положения точек Cc и Ci принадлежащих звеньям содержащихся в структуре механизма-прототипа ЭМК, а нижний индекс указывает на вид звена.
Столбцовые матрицы, содержащиеся в уравнениях системы (1) для сепаратора (водило) и i-го тела качения механизма-прототипа ЭМК
Матрицы вращения (поворота), содержащиеся в уравнениях системы (1) относительно неподвижной системы координат X(в)O(в)Y(в) для сепаратора (водило) и i-го тела качения механизма-прототипа ЭМК
Матрица вращения (поворота) и перемещения (сдвига), содержащаяся в уравнениях системы (1) относительно неподвижной системы координат X(в)O(в)Y(в) для i-го тела качения механизма-прототипа ЭМК
Подставив матрицы вращения (поворота) и перемещения (сдвига) (2)…(6) в систему уравнений (1) и преобразовав, получим:
В результате преобразования равенств (7) и (8) сформируем системы параметрических уравнений
здесь
![]() ,
,
![]() ,
,
![]() и
и
![]() —
координаты точек Cc и Ci
принадлежащих сепаратору (водило) и рабочей поверхности i-ого
тела качения относительно неподвижной системы координат X(в)O(в)Y(в).
—
координаты точек Cc и Ci
принадлежащих сепаратору (водило) и рабочей поверхности i-ого
тела качения относительно неподвижной системы координат X(в)O(в)Y(в).
Анализ систем (9)…(10) показывает, что данные системы параметрических уравнений являются математическими моделями сепаратора (водило) и тел качения содержащихся в структуре механизма-прототипа ЭМК при ведущем внутреннем кольце относительно неподвижной системы координат X(в)O(в)Y(в).
В результате решения систем параметрических уравнений (9)…(10) получим координаты любых точек лежащих на рабочих поверхностях тел качения и дорожек качения наружного и внутреннего колец, а также кривые второго порядка соответствующие рабочим поверхностям этих звеньев при наличии сепаратора (водило) в структуре механизма-прототипа ЭМК.
С целью повышения эффективности процесса решения систем параметрических уравнений (9)…(10) авторами разработано программное обеспечение [9, 10], которое представляет собой совокупность программных комплексов: «Эксцентрик», «ЭПМ V1» и «ЭПМV1.01» зарегистрированных в Реестре программ для ЭВМ Федеральной службы по интеллектуальной собственности (РОСПАТЕНТ) [11–13]. Представленные программные комплексы позволяют не только рассчитать координаты положения тел качения и точек их контакта с дорожками качения наружного и внутреннего колец, но и выполнить графическое моделирование всех видов симметричных схем, как механизма-прототипа, так и эксцентрикового механизма качения.
В результате представленных действий получены системы параметрических уравнений (9)…(10) совместно составляющие математическую модель механизма-прототипа ЭМК с сепаратором (водило) при ведущем внутреннем кольце. Решение математической модели дает возможность однозначного определения положений звеньев механизма-прототипа ЭМК на плоскости в требуемый момент времени, что создает возможность получения приемлемого решения задачи о положениях его звеньев и обеспечить реализацию заданного закона движения выходного звена исполнительного механизма технологического оборудования с наименьшими погрешностями.
Литература:
Мерко М. А., Меснянкин М. В., Шемякин Д. В., Леонтьев А. С., Собко И. В. Особенности формирования математической модели ЭМК при ведущем наружном кольце // Молодежь и наука: сборник материалов VII-ой Всероссийской научно-технической конференции студентов, аспирантов и молодых ученых посвященной 50-летию первого полета человека в космос [Электронный ресурс] / отв. ред. О. А. Краев — Красноярск: Сиб. фед. ун-т, 2011. — Режим доступа: http://conf.sfu-kras.ru/sites/mn2011/thesis/s19/ Shemyakin.pdf.
Меснянкин М. В., Мерко М. А., Колотов А. В., Беляков Е. В., Белякова С. А. Математическая модель ЭМК с сепаратором при ведущем внутреннем кольце // Сборник научных трудов Sworld по материалам международной научно-практической конференции. 2012. Т. 5. № 4. С. 62–67.
Мерко М. А. Кинематические и геометрические характеристики эксцентрикового механизма качения: автореф. дис. канд. техн. наук: 05.02.02. Красноярск, 2002. 26 с.
Мерко М. А., Меснянкин М. В., Митяев А. Е., Колотов А. В. Анализ взаимозависимостей геометрических параметров эксцентрикового механизма качения // Вестник Красноярского государственного аграрного университета. 2012. № 11. С. 180–184.
Беляков Е. В., Мерко М. А., Колотов А. В., Меснянкин М. В., Митяев А. Е. Обеспечение требуемого движения выходного звена эксцентрикового эпициклического механизма // Сборник научных трудов Sworld по материалам международной научно-практической конференции. 2012. Т. 5. № 4. С. 47–51.
Белякова С. А., Груздев Д. Е., Беляков А. Н., Мерко М. А., Меснянкин М. В., Колотов А. В. Применение дифференциального механизма для шлифования плоских поверхностей // Сборник научных трудов Sworld по материалам международной научно-практической конференции. 2012. Т. 5. № 4. С. 51–56.
Меснянкин М. В., Мерко М. А., Колотов А. В., Митяев А. Е. Определение границ областей существования механизмов-прототипов ЭМК при вводе поправки в расчет по дорожке качения внутреннего кольца // Вестник Красноярского государственного аграрного университета.2012. № 12.С.138–141.
Пискунов Н. С. Дифференциальное и интегральное исчисления для вузов. В 2 т. Т. 2: учеб. пособие для вузов. М: Наука, 1985. 560 с.
Мерко М. А., Меснянкин М. В., Файзиев А. Н., Вацлавский Е. С. Повешение эффективности проектирования эксцентриковых механизмов приводов технологического оборудования на основе ЭМК // Молодежь и наука: сборник материалов VII-ой Всероссийской научно-технической конференции студентов, аспирантов и молодых ученых посвященной 50-летию первого полета человека в космос [Электронный ресурс] / отв. ред. О. А. Краев — Красноярск: Сиб. фед. ун-т, 2011. — Режим доступа: http://conf.sfu-kras.ru/sites/ mn2011/thesis/s19/Faiziev.pdf
Беляков Е. В., Колотов А. В., Применение САПР при исследовании эксцентрикового планетарного механизма // Современные технологии. Системный анализ. Моделирование. 2012. № 3. С. 109–112.
Свидетельство о государственной регистрации программы для ЭВМ № 2012614197. Программный комплекс «Эксцентрик» / Меснянкин А. В., Мерко М. А., Колотов А. В., Груздев Д. Е., Митяев А. Е., Беляков Е. В.; заявитель и правообладатель ФГАОУ ВПО «Сибирский федеральный университет»; заявка № 2012612100 от 22.03.12; зарегистрировано в Реестре программ для ЭВМ 12.05.12.
Свидетельство о государственной регистрации программы для ЭВМ № 2012614355. Программный комплекс «ЭПМ V1» / Беляков Е. В., Мерко М. А., Колотов А. В., Груздев Д. Е., Митяев А. Е., Меснянкин А. В.; заявитель и правообладатель ФГАОУ ВПО «Сибирский федеральный университет»; заявка № 2012612237 от 27.03.12; зарегистрировано в Реестре программ для ЭВМ 16.05.12.
Свидетельство о государственной регистрации программы для ЭВМ № 2013610142. Программный комплекс «ЭПМV1.01» / Беляков Е. В., Мерко М. А., Колотов А. В., Груздев Д. Е., Митяев А. Е., Меснянкин А. В.; заявитель и правообладатель ФГАОУ ВПО «Сибирский федеральный университет»; заявка № 2012660154 от 23.11.12; зарегистрировано в Реестре программ для ЭВМ 09.01.13.