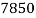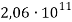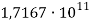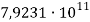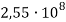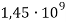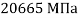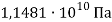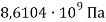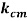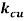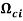Для анализа напряженно-деформированного состояния трубобетонной колонны круглого сечения была выполнена конечно-элементная модель в программном комплексе Ansys Workbench с учетом физической, геометрической и контактной нелинейности. Полученная расчетная модель достоверно отражает работу трубобетонных конструкций и может быть использована для дальнейших исследований.
Ключевые слова: трубобетон, трубобетонные сжатые колонны, модель Друкера — Прагера с учетом упрочнения/разупрочнения, нелинейная работа конструкций.
Одним из способов увеличения прочности бетона является применение стальных труб, выступающих в роли оболочки для бетонного ядра. Такие конструкции называются трубобетонными (ТБК).
Исследование ТБК началось еще в начале XX века и продолжается по сегодняшний день. Трубобетонные конструкции в современном строительстве нашли широкое применение, так как обладают конструкционными, эксплуатационными, технологическими и экономическими преимуществами. Важной особенностью таких конструкций является то, что несущая способность при совместной работе трубы и бетонного ядра выше, чем их суммарная несущая способность по отдельности.
Теоретическое определение напряжений в бетоне и трубе ТБК представляет сложную задачу. Такие ученые как Росновский В. А. [1], Лукша Л. К. [2], Кикин А.И [3], Кришан А. Л. [4], Стороженко Л. И. [5], Маренин В. Ф. [6], Санжаровский Р. С. [7] и другие исследовали работу трубобетонных конструкций на основе результатов испытаний опытных образцов. Но все полученные результаты справедливы только для тех условий, в которых они были получены. Поэтому необходимо создать конечно-элементную модель трубобетонной конструкции, которая при известных физико-механических свойствах материалов позволит вычислить развивающиеся деформации и напряжения в зависимости от напряженного состояния конструкции.
Одним из современных вычислительных комплексов, в котором доступен расчет нелинейных задач на основе конечно-элементного метода, является программный комплекс Ansys Workbench.
Трубобетонные конструкции характеризуются своей пластичной работой при приложении нагрузки. В работе таких конструкции встречаются все 3 вида нелинейности: геометрическая, физическая и контактная.
Геометрическая нелинейность конструкции заключается в непропорциональной зависимости между нагрузкой и перемещениями, вызванными деформированием конструкции. Математическая модель, с помощью которой возможно учесть большие перемещения, деформации, прогибы и изменение эффективной жесткости при изгибе, активируется с помощью метода Ньютона-Рафсона (Newton-Raphson Option). Данный метод является итерационным методом решения нелинейных задач. На каждом этапе загружения программа выполняет решение системы линейных уравнений, на основе которых вычисляется приращения перемещений, и вычисляет вектор внутренних сил, при котором система находится в равновесии [8].
Также геометрическая нелинейность учитывается за счет активированной опции Large Deflection, которая позволяет учитывать большие деформации, перемещения и углы поворота в конструкции [8].
Физической нелинейностью называется непропорциональная зависимость между напряжениями и деформациями. Для описания нелинейного поведения стали была применена модель с изотропным упрочнением и билинейная диаграмма зависимости напряжений от деформаций с изгибом на пределе прочности (рисунок 1). Для моделирования процесса пластического деформирования бетона задана нелинейной диаграммой деформирования бетона по приложению Г [9] (рисунок 2) с помощью модели Друкера — Прагера с экспоненциальным упрочнением/разупрочнением (softening).
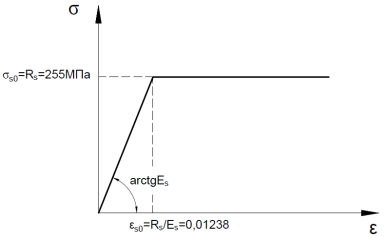
Рис. 1. Билинейная диаграмма зависимости напряжений от деформаций для стали
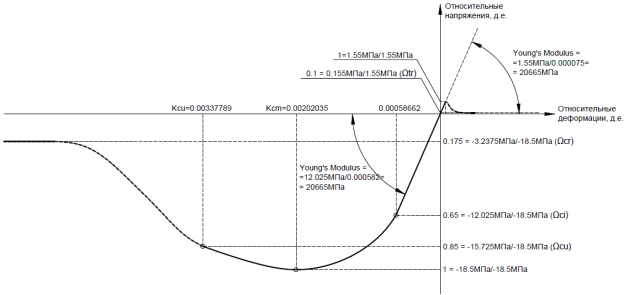
Рис. 2. Криволинейная диаграмма деформирования бетона В25
Модель Друкера — Прагера подходит для модели бетона в составе трубобетонной колонны, так как основывается на предположении трехосного расширения и на теории пластического течения.
Для верификации нелинейной модели бетона в Ansys Workbench был выполнен расчет эталонной призмы размерами 150х150х600 мм выполненной из бетона класса В25 [10], прочность при осевом сжатии которого составляет 18,5 МПа [9]. Несущая способность призмы составила 18,51 МПа, то есть разрушение призмы происходит при величине нагрузки чуть больше эталонной. Также были получены максимальные относительные деформации при сжатии на последней стадии работы образца, которые составляют 0,00384, что очень близко к рассчитанному значению 0,00338. Следовательно, можно сделать вывод, что модель Друкера — Прагера с учетом упрочнения-разупрочнения является наиболее подходящей для описания нелинейной работы бетона.
В качестве моделирования конструкции бетонного ядра и стальной оболочки использовался объемный конечный элемент SOLID186, в котором в перемещениях учитывается поступательные степени свободы, а также вводится дополнительная степень свободы — давление [8].
Контактная нелинейность характеризуется изменением статуса контакта, то есть от статуса контакта на соответствующем шаге нагружения зависит жесткость системы [8]. Для описания работы трубобетонной колонны в компьютерной модели взаимодействие бетона и трубы было задано через тип контакта Frictional — нелинейный тип контакта, который моделирует сцепление с коэффициентом трения. Коэффициент трения бетона о сталь был принят равным 0,47. Для моделирования контактной пары между поверхность бетона и трубы были применены следующие типы конечных элементов:
– CONTA174 для бетона;
– TARGE170 для стали.
В Ansys Workbench была создана модель короткого трубобетонного образца высотой 1м, диаметром 159мм и толщиной оболочки 3мм. Заданные материалы представлены в таблицах 1 и 2.
Таблица 1
Физико-механические свойства материала стали
|
Плотность, кг/м 3 |
Модуль упругости, Па |
Модуль объемных деформаций, Па |
Модуль сдвига, Па |
Коэф-фициент Пуассона |
Предел текучести, Па |
Касательный модуль, Па |
|
|
|
|
|
0,3 |
|
|
Таблица 2
Физико-механические свойства бетона
|
Характеристика |
Значение |
|
Плотность |
2400 кг/м3 |
|
Модуль упругости |
|
|
Коэффициент Пуассона |
0,2 |
|
Модуль объемных деформаций |
|
|
Модуль сдвига |
|
|
Предел прочности бетона при одноосном сжатии |
18,5 МПа |
|
Предел прочности бетона при одноосном растяжении |
1,55 МПа |
|
Предел прочности бетона при двухосном сжатии |
22,2 МПа |
|
Дилатансия растяжения и растяжения-сжатия |
0,25 |
|
Дилатансия сжатия |
1 |
|
Пластические относительные деформации при одноосном сжатии,
|
0,00143373 |
|
Полные относительные деформации при переходе от степенного к экспоненциальному размягчению,
|
0,00279127 |
|
Относительные напряжения в начале нелинейного упрочнения,
|
0,65 |
|
Остаточное относительное напряжения при переходе от степенного закона к экспоненциальному размягчению,
|
0,85 |
|
Остаточное относительное напряжение при сжатии,
|
0,175 |
|
Энергия разрушения |
155,55 |
|
Остаточное относительное напряжение при растяжении |
0,1 |
Нижний торец трубобетонной колонны был закреплен от смещения и поворота (Fixed Support), а на верхний торец образца (на все сечение) было приложено заданное перемещение (Displacement). Также был задан собственный вес конструкции (рисунок 3).

Рис. 3. Расчетная модель трубобетонной колонны круглого сечения
В результате была получен график зависимости деформаций от нагрузки (рисунок 4).
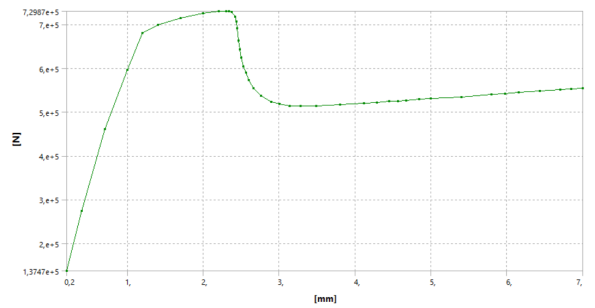
Рис. 4. График зависимости перемещений от нагрузки ТБК d159t3
Полученная диаграмма деформирования ТБК схожа с диаграммами, полученными другими авторами [1, 4]. Картина деформирования трубобетонного элемента (рисунок 5) похожа на деформированные образцы, полученные при испытаниях Росновского [1].
а)
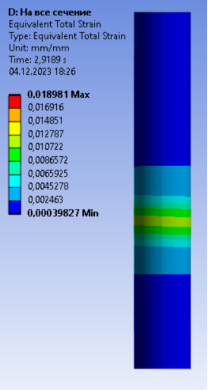
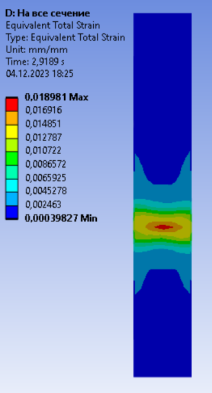
Рис. 5. Распределение суммарных эквивалентных деформаций: a) в стальной оболочке; б) в бетонном ядре
При приложении нагрузки образец сначала деформируется упруго, затем при относительных деформациях 0,7–2,3 мм/м в образце появляются пластические деформации. При достижении пластических деформаций выше 2,3 мм/м происходит резкое снижение несущей способности, бетон принимает форму бочки, появляются характерные поперечные складки на трубе и образец разрушается.
В результате расчета предельная нагрузка на испытуемый образец составила:
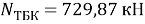
Значение предельной нагрузки, рассчитанное по своду правил [11]:
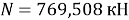
Разница составляет 5 %.
Суммарное предельное усилие стальной оболочки и бетонного цилиндра:
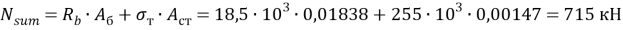
Так как
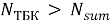
Предельная нагрузка на бетонный цилиндр диаметром 153 мм:
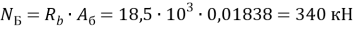
Также была вычислена несущая способность для железобетонной колонны диаметром 153 мм с таким же процентом армирования
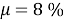
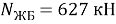
Следовательно, применение данной трубобетонной колонны дает увеличение несущей способности в 2,14 раза по сравнению с бетонным неармированным цилиндром и в 1,2 раза по сравнению с железобетонной колонной с таким же процентом армирования, что соответствует выводам других авторов.
Таким образом,была создана и описана конечно-элементная модель образца трубобетонной колонны круглого сечения, которая достоверно отображает работу ТБК. Следовательно, полученная расчетная модель может быть использована для дальнейших исследований.
Литература:
- Росновский В. А. Трубобетон в мостостроении. М., Трансжелдориздат, 1963, 109с.
- Лукша Л. К. Прочность трубобетона. Мн., «Высшая школа», 1977, 96с.
- Кикин А. И., Санжаровский Р. С., Трулль В. А. Конструкции из стальных труб, заполненных бетоном. М., Стройиздат, 1974, 144с.
- Кришан А. Л., Римшин В. И., Астафьева М. А. Сжатые трубобетонные элементы. Теория и практика: монография. М.: Издательство АСВ, 2020, 322с.
- Стороженко Л. И., Плахотный П. И., Черный А. Я. Расчет трубобетонных конструкций. К.:Будивэльнык, 1991, 120 с.
- Маренин В. Ф. Исследование прочности стальных труб, заполненных бетоном при осевом сжатии: дис. канд. техн. наук. М., 1959. 291 с.
- Санжаровский Р. С. Теория и расчет прочности и устойчивости элементов конструкций из стальных труб, заполненных бетоном. Автореферат дис. на соискание ученой степени доктора технических наук / Ленингр.инж.-строит. Ин-т. — Ленинград: 1974, 55с.
- Федорова Н. Н., Вальгер С. А., Данилов М. Н., Захарова Ю. В. Основы работы в ANSYS 17. М.: ДМК Пресс, 2017, 210с.
- СП 63.13330.2018 «Бетонные и железобетонные конструкции. Основные положения». Актуализированная редакция СНиП 52–01–2003 (с Изменениями № 1,2). [Электронный ресурс]. ИС «Техэксперт» (дата обращения 01.04.2022).
- ГОСТ 10180–2012 «Бетоны. Методы определения прочности по контрольным образцам». [Электронный ресурс]. ИС «Техэксперт» (дата обращения 01.05.2023).
- СП 266.1325800.2016 «Конструкции сталежелезобетонные. Правила проектирования» (с Изменениями № 1,2,3, с Поправками). [Электронный ресурс]. ИС «Техэксперт» (дата обращения 01.02.2022).