В статье рассматриваются основные модели биполярных транзисторов в современных вычислительных программных средствах, их схемы и особенности работы каждой из них.
Ключевые слова: биполярный транзистор, эквивалентные схемы, модель Эберса — Молла, транспортная модель, модель Гуммеля — Пуна..
Нелинейные физические модели
Простейшей моделью биполярного транзистора, основанной на физических соображениях, является модель Эберса — Молла, в основу которой положена диодная эквивалентная схема. Ради большей точности моделирования выполняется преобразование, которое сначала приводит к транспортной модели, а после ввода дополнительных характеристик даёт модель Гуммеля — Пуна, которая позволяет весьма точно описывает транзистор и применяется в программах компьютерного проектирования.
Модель Эберса — Молла
Одной из наиболее распространенных физических моделей биполярных транзисторов является модель Эберса — Молла. В данной модели переходы транзистора представляются в виде двух диодов, включенных встречно. Также присутствуют два управляемых источника тока, которые описывают протекающий через базу ток. Коэффициенты N и I являются коэффициентами передачи тока в нормальном и инверсном режимах соответственно. Модель Эберса — Молла не учитывает объёмные сопротивления, которые значительно усложнят систему уравнений. Схема модели изображена на рисунке 1.
![Модель Эберса — Молла для n-p-n транзистора [5]](https://moluch.ru/blmcbn/110765/110765.001.png)
Рис. 1. Модель Эберса — Молла для n-p-n транзистора [5]
Для получения уравнений, описывающих данную модель, применим первый закон Кирхгофа.
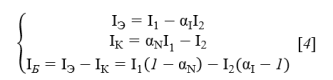
где
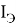
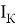
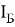
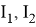
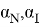
Идеальная вольтамперная характеристика p-n перехода описывается следующими формулами:
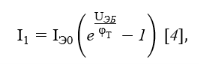
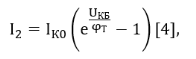
где
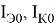
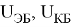
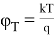
Подставив формулы (2), (3) в формулу (1), получим:
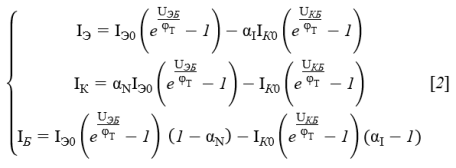
Согласно теореме об обратимости цепей:
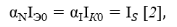
где
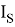
Таким образом, модель Эберса — Молла описывается только тремя параметрами N , I , I S и является идеализированной. Она не учитывает объемные сопротивления полупроводниковых областей, ток рекомбинации эмиттерного перехода, эффект Эрли — модуляцию толщины базы. Рассмотренная модель определяет только статические характеристики, поэтому ее называют статической моделью.
Модель Эберса — Молла также обладает и достоинствами, которые делают её полезной и широко используемой в проектировании усилительных схем с биполярными транзисторами. Данная модель является наименее сложной, что делает её легкой для понимания и использования. Модель Эберса — Молла, несмотря на её приближенность, очень полезна для анализа статических режимов при больших изменениях сигналов, так как она нелинейная.
Транспортная модель
Транспортная модель получается из рассмотренной ранее модели Эберса — Молла путём эквивалентного преобразования. В ней вместо двух управляемых источников тока содержится только один. Схема данной модели приведена на рисунке 1.2.
![Транспортная модель n-p-n транзистора [5]](https://moluch.ru/blmcbn/110765/110765.016.png)
Рис. 2. Транспортная модель n-p-n транзистора [5]
В данной модели важными являются коэффициенты передачи тока базы N , I в нормальном и инверсном режимах соответственно. Они связаны с коэффициентами N и I следующими выражениями:
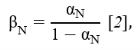
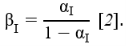
Токи в схеме, изображенной на рисунке 2, определяются
формулами (8), (9), (10).
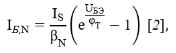
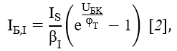
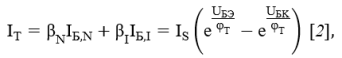
где
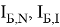
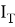
Тогда для транспортной модели получим систему уравнений:
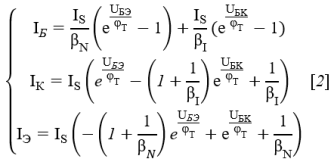
Транспортная модель, как и модель Эберса — Молла, отображает статические характеристики биполярного транзистора. Она описывается тремя параметрами I S , N , I . Модель является упрощенной, а уравнения, описывающие её, тождественны уравнения модели Эберса — Молла с учетом связи между коэффициентами. Основным отличием транспортной модели является то, что она отдельно рассматривает ток переноса заряда через базу транзистора.
Уточненная транспортная модель
Транспортную модель уточняют, чтобы она учитывала токи утечки, эффект Эрли и эффект сильного тока.
Для описания токов утечки в модель вводят ещё два диода с токами:
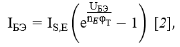
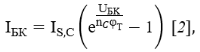
где
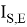
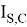
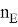
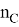
Эффект Эрли и эффект сильного тока влияют на ток переноса, поэтому для описания этого влияния вводится безразмерная величина q B , которая служит мерой относительного заряда основных носителей в базе. Тогда ток переноса:
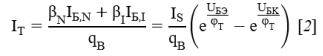
Таким образом уточнённая транспортная модель, представленная на рисунке 1.3, характеризуется выражениями:
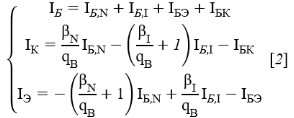
![Уточнённая транспортная модель для n-p-n транзистора [5]](https://moluch.ru/blmcbn/110765/110765.033.png)
Рис. 3. Уточнённая транспортная модель для n-p-n транзистора [5]
Модель Гуммеля — Пуна
Дальнейшее уточнение транспортной модели приводит к получению модели Гуммеля — Пуна, изображенной на рисунке 1.4
![Модель Гуммеля — Пуна для n-p-n транзистора [5]](https://moluch.ru/blmcbn/110765/110765.034.png)
Рис. 4. Модель Гуммеля — Пуна для n-p-n транзистора [5]
В данной модели:
R Б , R Э , R К — объёмные сопротивления базы, эмиттера, коллектора,
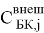
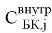
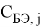
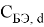
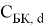
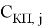
Модель Гуммеля — Пуна описывает кроме ранее рассмотренных эффектов (тока утечки, эффекта Эрли и др.) ещё и зависимость коэффициента передачи тока базы от тока коллектора, объемные сопротивления, барьерные и диффузионные ёмкости, влияние подложки.
Таким образом, модель Гуммеля — Пуна обладает высокой точностью и позволяет учитывать многие физические эффекты, однако она требует большое число параметров, что делает ее сложной для анализа. Поэтому данная модель в основном используется в компьютерных программах для моделирования электронных схем, например, в программах PSpice, OrCAD.
Литература:
- А. Н. Флёров. Схемотехника аналоговых электронных устройств. СПб. БГТУ «ВОЕНМЕХ» им. Д. Ф. Устинова, 2023, эл. рес.
- Титце У., Шенк К. Полупроводниковая схемотехника. 12-е изд. Том I: Пер. с нем. — М.: ДМК Пресс, 2008. — 832 с.
- Электронные приборы. Под ред. Шишкина Г. Г. Учебник для ВУЗов — М: Энергоатомиздат, 1989.
- Гусев В. Г., Электроника и микропроцессорная техника. 6-е изд., стер. — М.: КНОРУС, 2013. — 800 с.
- Петров, М. Н. Моделирование компонентов и элементов интегральных схем: учебное пособие для вузов / М. Н. Петров, Г. В. Гудков. — 2-е изд., стер. — Санкт-Петербург: Лань, 2021. — 464 с.







