Рассмотрим упрощенную математическую модель краевой задачи [1, с.1]. Потенциальная энергия деформации включения записывается в виде

где
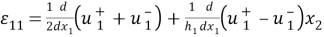
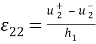
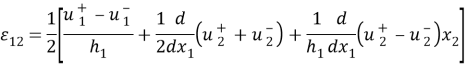
Подставим в (1) выражения (2) и осуществим интегрирование по
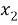
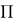

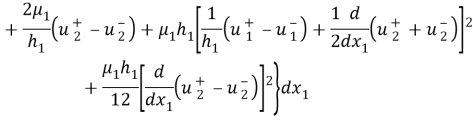
Теперь предположим, что величины
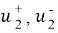
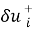
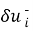
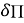
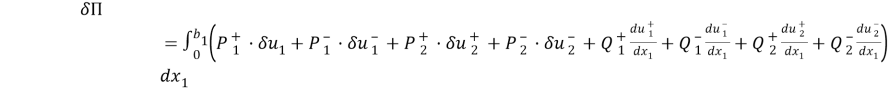
Здесь

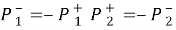
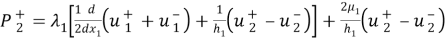




Интегрированием по частям приведем выражение для
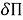
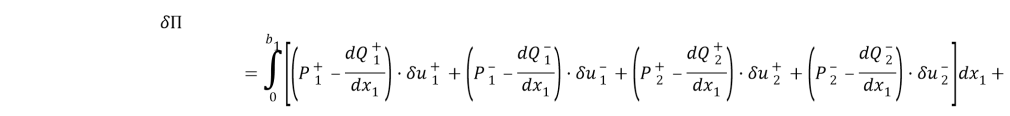
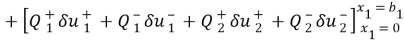
Аппроксимируем теперь аналогичным образом кинетическую энергию включения

В соответствии с соотношениями
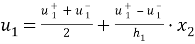
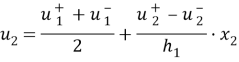
имеем
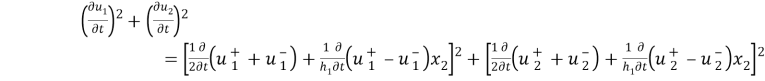
Осуществляя интегрирование по
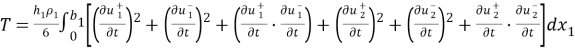
Отсюда следует, что при приращениях
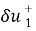
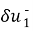
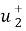
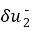
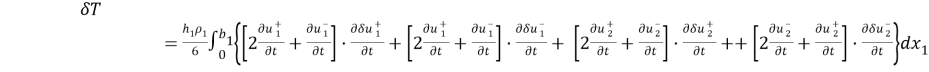
Пусть t >0. Тогда

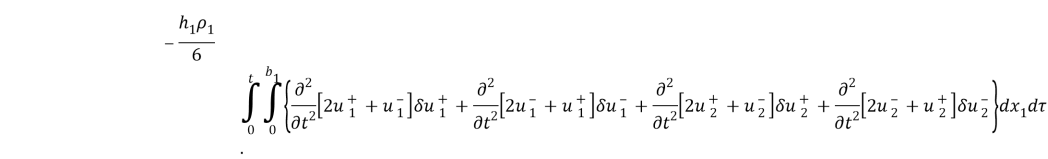
Теперь для нахождения условий на включении, которая интерпретируется как линия 0
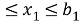
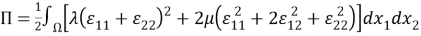
Выражения для
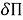
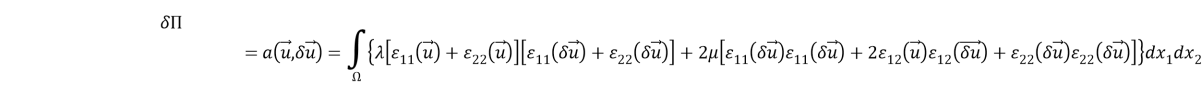
Отметим формулу Грина

Здесь

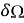
Разделим область

Тогда, согласно формуле Грина:
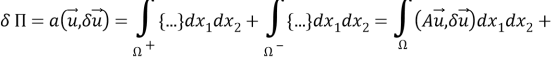
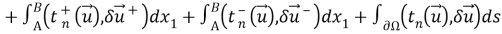
Здесь учтено, что

Согласно принципа Гамильтона для любого t>0 должно выполняться вариационное равенство
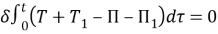
Сюда надо подставить выражение для
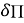
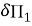
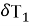
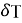

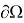
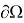
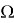
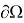
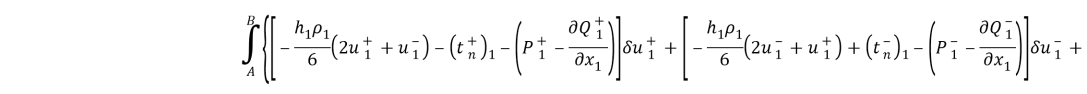
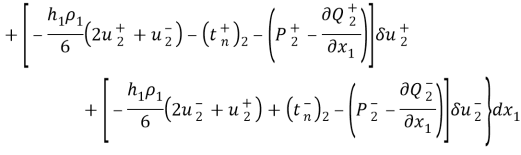
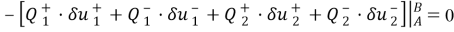
В выражениях

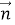
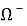

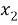

Здесь

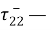
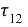

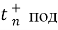


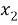

С учетом (8), (9) из (7) вытекает, что вдоль линии АВ должны выполняться четыре уравнения
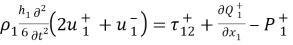
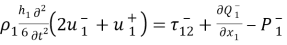
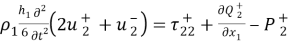
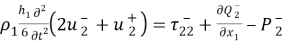
В конечных точках А и В должны выполняться естественные граничные условия
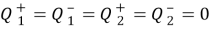
Литература:
- Международный научный журнал «Молодой ученый» № 2 (501), 12 январь 2024 г., URL:https://moluch.ru/archive/501/110161/.
- Купрадзе В. Д. Методы потенциала в теории упругости. — М.: Физматгиз, 1963. — 472 с.
- Механика деформируемых твердых тел: Направления развития. Сб. статей: Пер. с англ. В. В. Шлимака/Под ред. Г. С. Шапиро — М.: Мир, 1983.







