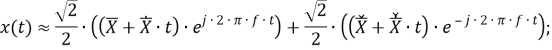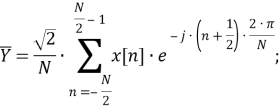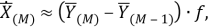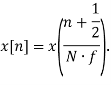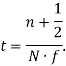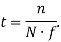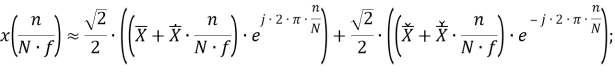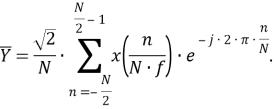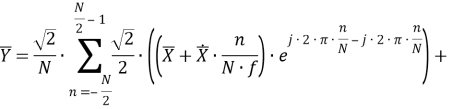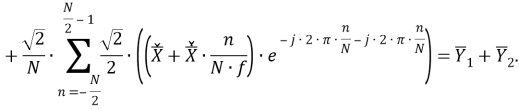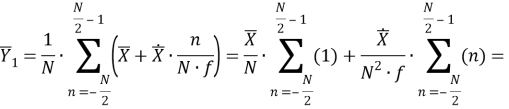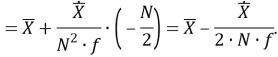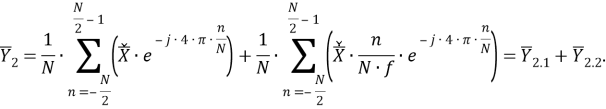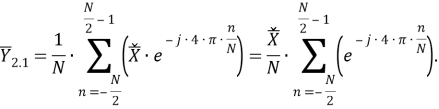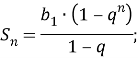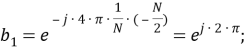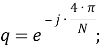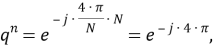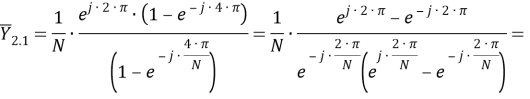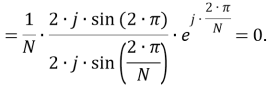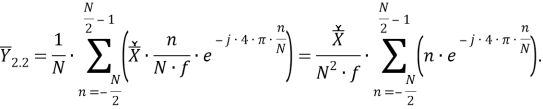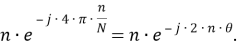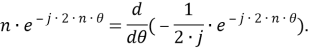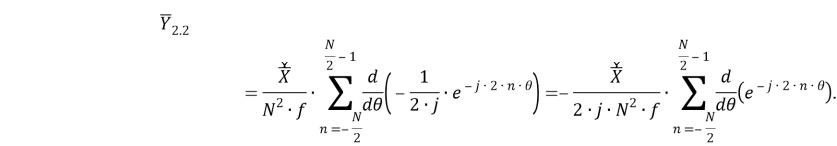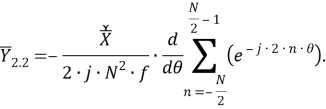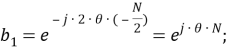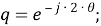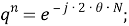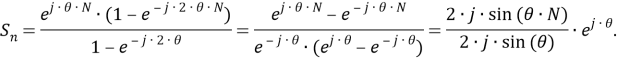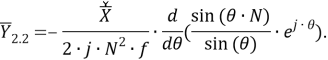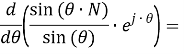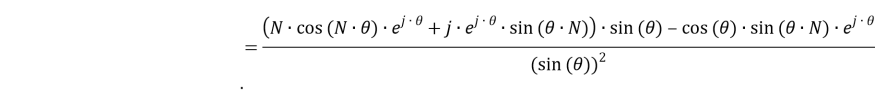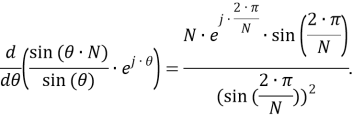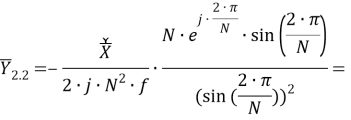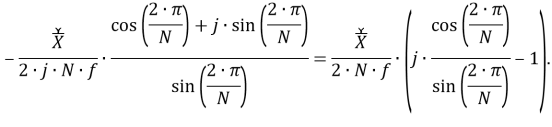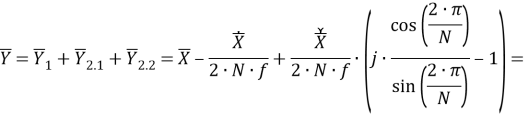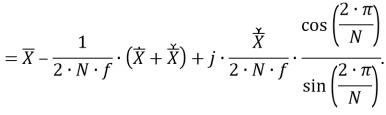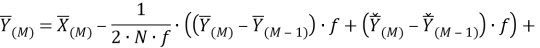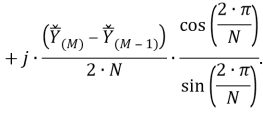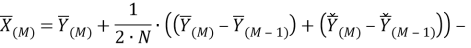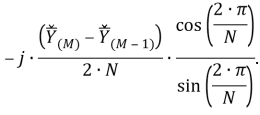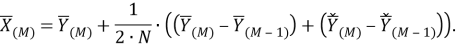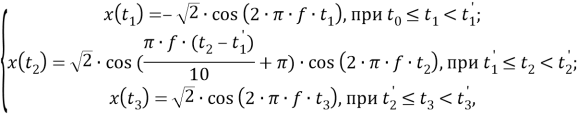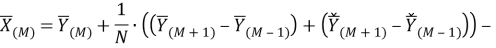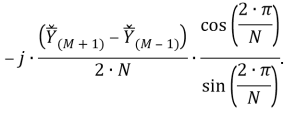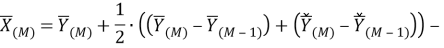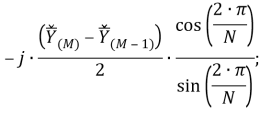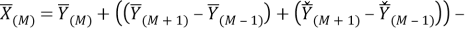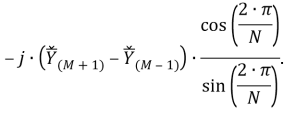Реализация и верификация модели цифрового фильтра устройства синхронизированных векторных измерений



Исследование вопроса применения синхронизированных векторных измерений (СВИ), зафиксированных во время быстропротекающих электромагнитных процессов, для решения различных задач требует наличия либо данных от реальных устройств СВИ (УСВИ), либо моделей их цифровых фильтров, позволяющих имитировать тракт обработки сигналов реальных УСВИ. Данная статья посвящена реализации и верификации одной из ранее предложенных моделей, ее модификации и исследованию функционирования. В результате разработаны и исследованы три модификации исследуемой модели фильтра УСВИ (помимо его базовой версии). Помимо этого, проведен сравнительный анализ эффективности их функционирования при фиксации токов и напряжений короткого замыкания в электрической сети сверхвысокого напряжения.

Ключевые слова: синхронизированные векторные измерения, цифровые фильтры устройств СВИ, переходный процесс.

Введение

Синхронизированные векторные измерения (СВИ) — относительно новое направление в электроэнергетике, являющееся одним из ключевых компонентов интеллектуальных электрических сетей « Smart Grids ». Суть технологии СВИ заключается в следующем:

— устройства СВИ (УСВИ), установленные на различных объектах электроэнергетической системы (ЭЭС), осуществляют преобразования мгновенных значений токов и напряжений в соответствующие вектора;

— вычисленным векторам УСВИ присваивает метки времени, принимая сигналы точного времени от глобальной спутниковой системы ( GPS / ГЛОНАСС);

— на основе вычисленных векторов определяется частота переменного тока, потоки мощностей, параметры отдельных последовательностей и прочее. Все указанные режимные параметры могут передаваться для хранения и последующего использования в концентраторы синхронизированных векторных данных.

В Единой энергетической системе России технология СВИ реализуется в рамках системы мониторинга переходных режимов. Данная система предназначена, в первую очередь, для анализа динамического поведения ЭЭС при электромеханических переходных процессах [1].

Традиционно считается, что УСВИ производят неточные измерения при быстропротекающих электромагнитных переходных процессах, например, при коротких замыканиях (КЗ) [2]. Однако результаты отечественных и зарубежных работ [3–5], посвященных исследованию этого вопроса и основанных на данных, зафиксированных реальными УСВИ, свидетельствуют о необходимости более полного исследования функционирования УСВИ при КЗ. Выявлено, что СВИ, зафиксированные при КЗ на воздушной линии, могут быть использованы, например, для решения задач определения места (ОМП) и типа повреждения.

Для получения объективных выводов касательно применимости УСВИ для задачи ОМП (и, в целом, задач релейной защиты и автоматики) требуется наличие либо реальных УСВИ, либо их верифицированных моделей (главным образом — моделей цифровых фильтров для выделения синхронизированных векторов). В стандарте [6] представлено описание двух различных фильтров УСВИ. Однако указанный стандарт не ограничивает производителей УСВИ применением описанных в нем расчетных выражений, а лишь предъявляет требования к статическим и динамическим характеристикам УСВИ при воздействии регламентированных тестовых сигналов. Поэтому, помимо представленных в [6] расчетных выражений, целесообразно также исследовать альтернативные модели фильтров УСВИ, что позволяет произвести более комплексный анализ применимости СВИ, например, в задаче ОМП. При этом необходимо учитывать, что детали реализации цифровых фильтров коммерческих УСВИ, как правило, не доступны. Поэтому в настоящем исследовании — в качестве альтернативы классическим моделям из [6] — рассматривается версия цифрового фильтра УСВИ из [7]. Основными задачами работы являются:

— анализ и реализация исходной версии модели цифрового фильтра из [7], подробное математическое описание которой в [7] отсутствует;

— разработка и реализация различных модификаций исходной версии;

— сравнительное тестирование реализованных моделей фильтра УСВИ.

Все вычислительные эксперименты выполняются в программно-вычислительном комплексе (ПВК) « MATLAB ».

1. Математическая модель исследуемого цифрового фильтра УСВИ

Рассматриваемый цифровой фильтр УСВИ основан на классическом однопериодном дискретном преобразовании Фурье (ДПФ) со скользящим прямоугольным окном. Основной особенностью фильтра является коррекция рассчитанного вектора, осуществляемая для его уточнения, при несоответствии фактического значения частоты номинальному. Нужно заметить, что вывод аналитических выражений, по которым осуществляется коррекция, в [7] не раскрыт, в связи с чем в рамках настоящей работы представлены подробные математические преобразования для модифицированного варианта алгоритма УСВИ. Еще одной немаловажной особенностью является то, что вектора по описанному алгоритму рассчитываются ровно на центр окна данных (при этом количество точек исходного сигнала, приходящихся на один период, — четное число). Например, если количество дискретных значений сигнала тока или напряжения, приходящихся на один период, равно 16, то метка времени рассчитанного вектора будет равна времени, соответствующему точке 8,5. В таком случае метка времени векторов никогда не будет равна времени, соответствующему какому-либо дискретному значению исходного сигнала. В моделях «классических» (описанных в стандарте [6]) фильтров ситуация обратная — метка времени рассчитанного вектора всегда равна времени, соответствующему какому-либо дискретному значению исходного сигнала. Это накладывает определенные ограничения на сравнение результатов расчета векторов при использовании «классических» и альтернативного фильтров. Поэтому при реализации альтернативного фильтра указанную особенность целесообразно нивелировать, что обсуждается в следующем разделе статьи. Математическую основу модели рассматриваемого фильтра составляют выражения (1) — (3):

	(1)
	(2)
	(3)

где — мгновенное значение исходного непрерывного сигнала;

— комплексное/векторное представление исходного синусоидального сигнала;

— первая производная комплексного представления исходного синусоидального сигнала по времени;

— время;

— частота исходного сигнала;

— сопряженные комплексы к и , соответственно;

— комплексное представление исходного дискретного сигнала, получаемое с помощью ДПФ (без каких-либо корректировок);

— количество дискретных значений исходного сигнала, приходящихся на один период;

— дискретные значения исходного сигнала, которые связаны с следующим образом:

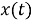
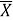
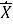
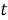
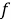
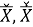
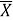
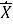
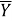
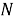
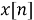
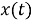
(4)

Математически сдвиг метки времени рассчитанного вектора на половину периода дискретизации исходного сигнала реализуется в представлении времени при переходе от исходного непрерывного сигнала к дискретному:

(5)

Для нивелирования описанной ранее особенности модели фильтра, выражение (5) приводится к следующему виду:

(6)

Тогда выражения (1), (2) перепишутся следующим образом:

	(7)
	(8)

Согласно алгоритму математического вывода модели фильтра УСВИ, представленному в [7], выражение (7) подставляется в правую часть (8):

(9)

Выражение (9) далее разбивается на две части. После этого отдельно рассматриваются выражения для входящих в него слагаемых и

:

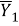
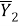
	(10)
	(11)

Слагаемое аналогичным образом разбивается на два слагаемых , . Выражение для выглядит следующим образом:

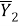
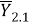
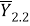
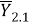
(12)

В выражении (12) то, что находится под знаком суммы ( ), является геометрической прогрессией (ГП). Сумма членов ГП определяется так, как показано ниже:

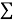
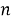
	(13)
	(14)
	(15)
	(16)

где — первый член ГП;

— знаменатель рассматриваемой ГП;

— знаменатель ГП, возведенный в степень, равную количеству членов рассматриваемого ряда.

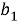
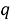
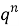
С учетом вышеизложенного выражение (12) примет следующий вид:

(17)

Далее рассматривается второе слагаемое выражения (11) — :

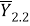
(18)

То, что в выражении (18) находится под знаком суммы ( ), необходимо преобразовать в ГП. Для этого введем обозначение . Тогда преобразуемая часть выражения (18) будет иметь следующий вид:

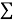
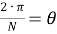
(19)

Затем преобразуется правая часть выражения (19):

(20)

С учетом этого выражение (18) перепишется следующим образом:

(21)

Поскольку сумма производных нескольких функций равна производной суммы этих функций, операцию дифференцирования можно вынести из-под знака суммы:

(22)

Теперь под знаком суммы находится ГП, для которой справедливы следующие выражения:

	(23)
	(24)
	(25)
	(26)

В результате выражение (22) примет следующий вид:

(27)

Дифференциал из выражения (27) определяется следующим образом:

(28)

Осуществляя обратную подстановку ( ), дифференциал из (28) преобразуется к виду:

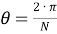
(29)

Тогда выражение (27) запишется следующим образом:

(30)

В итоге выражение (9) примет следующий вид:

(31)

Далее выражение (3) подставляется в выражение (31):

(32)

Из (32) получается формула, определяющая итоговый скорректированный вектор:

(33)

В процессе верификации полученной модели в форме (33) выявлено, что вектор «без корректировки» определяется вещественной частью выражения (33):

(34)

Полученное выражение (33) используется в качестве базовой версии алгоритма, реализующего альтернативный (по отношению к [6]) фильтр УСВИ.

2. Результаты верификации базовой математической модели цифрового фильтра УСВИ

Описанная модель цифрового фильтра УСВИ была реализована в ПВК « MATLAB ». В [7] представлена реакция исследуемой исходной версии модели фильтра УСВИ на два сигнала: косинусоидальный сигнал неноминальный частоты (в [7] номинальная частота электрической сети принимается равной 60 Гц), а также на косинусоидальный сигнал («Cosine Ramp»), действующее значение которого изменяется от –1 до 1 в течение 10 периодов, как функция косинуса. Указанный сигнал описывается выражением:

(35)

где — номинальная частота сигнала, 60 Гц;

— начальное значение времени для первой части функции;

— конечные значения времени для первой, второй и третьей частей функции, соответственно.

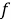
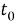
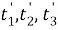
Верификация реализованной модели фильтра осуществляется путем сравнения ее реакции на указанные сигналы с соответствующим откликом модели, представленным в [7]. На рисунке 1 представлены графики, характеризующие динамические свойства реализованного цифрового фильтра, из полного совпадения которых с аналогичными графиками в [7] можно сделать вывод о корректности реализации фильтра в виде (33).

Рис. 1. Результаты верификации фильтра УСВИ из [7]

3. Модификация расчетного выражения цифрового фильтра УСВИ и сравнительный анализ выражений

В представленной ранее модели альтернативного фильтра УСВИ, определяемой выражением (33), производная рассчитываемого вектора определяется по двум «классически» рассчитанным векторам и , между которыми расстояние по времени составляет один период исходного сигнала (выражение (3)). Помимо базовой версии модели фильтра в рамках настоящего исследования были также реализованы три ее дополнительные модификации. Суть модификаций заключается в определении производной искомого вектора .

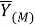
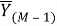
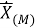
Во второй версии модели фильтра производная определяется по векторам и

, между которыми расстояние во времени составляет два периода исходного сигнала. При этом выражение для определения вектора записывается следующим образом:

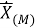
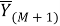
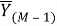
(36)

В третьей и четвертой версии модели фильтра указанная производная определяется по аналогичным первым двум версиям принципам, но расстояние во времени между рассчитанными векторами составляет, соответственно, один и два периода дискретизации исходного сигнала. Итоговые выражения при этом имеют следующий вид:

	(37)
	(38)

Сравнение эффективности реализованных моделей данного фильтра, а также наиболее простой модели, основанной на однопериодном ДПФ, осуществлялось путем обработки всеми моделями фильтров осциллограмм токов и напряжений, полученных при расчете различных сценариев КЗ в моделях ЭЭС, реализованных в ПВК « Simulink ». Основным показателем при сравнении является полная векторная погрешность рассчитанных векторов (« TVE ») [6]. В большинстве случаев третья модификация фильтра, описываемая выражением (37), либо не уступала остальным в точности фиксации векторов, либо была точнее. Результаты сравнения « TVE », рассчитанных по осциллограммам токов и напряжений поврежденной фазы при одном из смоделированных однофазных КЗ в модели ЭЭС 750 кВ, представлен на рисунке 2.

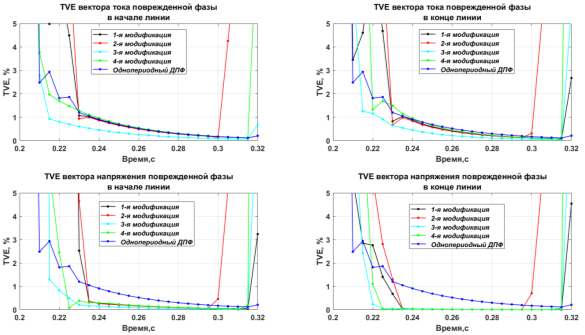
Рис. 2. Результаты сравнения различных модификаций цифрового

фильтра УСВИ, базовая версия которого представлена в [7]

Заключение

В ходе выполнения исследования проанализирована, реализована и успешно верифицирована модель цифрового фильтра УСВИ, описанная в [7]. Вывод об успешной верификации сделан на основе полного совпадения реакции реализованной модели фильтра на определенные сигналы с соответствующей реакцией, представленной в [7]. На основе данной модели разработаны три ее дополнительные модификации. Сравнительный анализ точности и скорости фиксации токов и напряжений при смоделированных однофазных КЗ в ЭЭС 750 кВ позволил выявить наиболее эффективную версию модели, описываемую выражением (37). Результаты исследования позволят получить более комплексные выводы касательно применимости СВИ для регистрации параметров электромагнитных переходных процессов в устройствах релейной защиты и автоматики.

Литература:

1. Онлайн-лекция «Технология векторной регистрации параметров электрического режима». Режим доступа: https://www.youtube.com/watch?v=a8GHJp4uZLE (дата обращения 05.02.2024 г.).
2. Phadke A. G., Thorp J. S. Synchronized Phasor Measurements and Their Applications. — Springer, 2017.
3. Определение места повреждения на воздушных линиях 500 кВ ЕЭС России по данным синхронизированных векторных измерений / И. Е. Иванов, Я. А. Умнов, А. В. Жуков, Д. М. Дубинин // Энергетик. — 2023. — № 7. — С. 31–39. — EDN YDDLIV.
4. P. Mukhopadhyay, R. Anumasula, A. Gartia, C. Kumar, P. Seshadri, and S. Patil, «Case study on fault analysis using PMU», in Proc. 2014 Eighteenth National Power Systems Conference (NPSC), pp. 1–6. https://doi.org/10.1109/NPSC.2014.7103778.
5. F. V. Lopes, A. Mouco, R. O. Fernandes, and F. C. Neto, «Real-World case studies on transmission line fault location feasibility by using M- Class phasor measurement units», Electrical Power Systems Research, vol. 196, pp. 1–7, April 2021. https://doi.org/10.1016/j.epsr.2021.107261.
6. IEEE/IEC International Standard — Measuring relays and protection equipment — Part 118–1: Synchrophasor for power systems — Measurements, in IEC/IEEE 60255–118–1:2018, pp. 1–78, December 2018. https://doi.org/10.1109/IEEESTD.2018.8577045.
7. J. Sykes, K. Koellner, W. Premerlani, B. Kasztenny, and M. Adamiak, «Synchrophasors: A primer and practical applications», in Proc. 2007 Power Systems Conference: Advanced Metering, Protection, Control, Communication, and Distributed Resources, Clemson, SC, USA, pp. 213–240. https://doi.org/10.1109/PSAMP.2007.4740914.