The purpose of this article is to find a way to implement a zero-knowledge proof based on the NP-hard problem of 3-coloring in the form of software while maintaining the efficiency condition of the algorithm.
Keywords: zero-knowledge proof, authentication, algorithm, graph, protocol, 3-coloring.
Целью данной статьи является поиск способа реализации доказательства с нулевым разглашением, основанного на NP-сложной задаче о трехцветной раскраске графа, в виде программного обеспечения с сохранением условия эффективности алгоритма.
Ключевые слова: доказательство с нулевым разглашением, аутентификация, алгоритм, граф, протокол, криптография, трехцветная раскраска.
The emergence of processes such as identification and authentication was due to the need to distinguish people according to various characteristics, to compare a person with a specific group of people, and to determine whether a person is who he is trying to impersonate.
The most common method of identity verification in information systems remains single-factor authentication with a password, but this method is not only the most widespread, but also one of the oldest. If in ancient times the password fulfilled the duties assigned to it, then in our time, with the growth of computing power, the problems of this authentication method are becoming more pronounced. A simple password is easy to remember, but also easy to pick up, therefore, to increase the complexity of selection, it is necessary to increase the complexity of the password, but as it increases, the difficulty to remember also increases in direct proportion. In addition, to pass the authentication procedure, it is necessary to provide the relying party with the password itself, which can have extremely undesirable consequences in the unlikely but very real case if the security of the authentication system is compromised.
The use of zero-knowledge proof in authentication systems will save them from the problems listed above.
In cryptography, a zero-knowledge proof or zero-knowledge protocol is a method by which one party (the prover) can prove to another party (the verifier) that a given statement is true while the prover avoids conveying any additional information apart from the fact that the statement is indeed true [1].
As is known, for any NP-complete problem there is no efficient solution algorithm, which means that on the basis of any NP-complete problem a zero-knowledge proof protocol can be constructed [2]. But there is a problem with programming the zero-knowledge proof.
Consider a zero-knowledge proof protocol based on the NP-complete 3-coloring problem [3]. The Prover claims to have a solution certificate for an instance of the 3-сoloring problem. He cannot simply disclose the solution certificate to the Verifier, the latter, in turn, cannot trust the Prover at his word and requires convincing evidence.
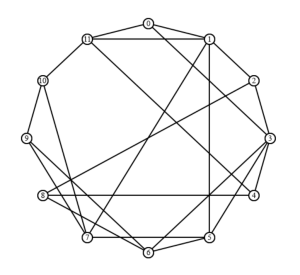
Fig. 1. An instance of the 3-coloring problem of G graph
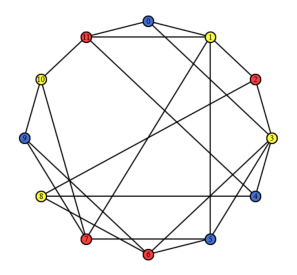
Fig. 2. Certificate of solving the problem of 3-coloring graph G
To solve this problem, a third trusted party can be involved in the protocol. In this case, the Prover and the Verifier fully trust the Trusted, all three parties have information about the structure of the graph, but only the Prover and the Trustee have absolutely identical versions of its three-color coloring, and the latter undertake to change the colors of the vertices identically with each iteration of the protocol. It is important to clarify that the Trusted, unlike the Prover, who can be «dishonest», always has the right solution.
The protocol begins with the Verifier choosing a random edge
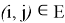
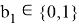
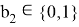
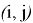
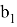
The Prover receive edge
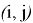
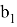
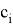
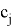
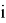
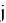
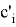
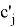
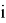
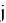
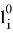
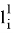
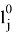
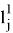
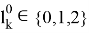
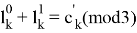
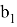
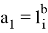
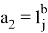
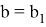
The Prover receives values
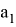
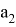
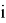
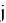
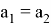
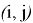
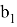
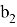
Trusted receives the edge
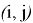
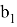
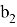
If
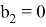
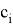
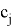
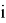
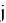
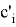
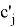
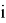
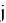
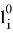
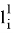
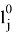
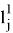
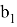
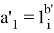
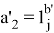
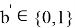
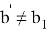
The Verifier receives values
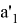
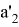
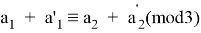
If
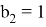
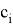
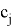
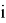
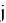
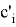
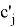
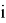
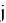
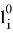
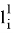
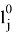
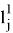
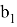
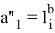
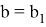
The Verifier receives value
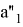
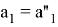
In conclusion, the idea of the article was to was to rethink the zero-knowledge proof based on the NP-complete 3-coloring problem and then apply this principle to create an authentication system that uses knowledge of the solution certificate in the process of authenticating subjects, which can become an alternative to password authentication methods.
References:
- Goldwasser S., Micali S., Rackoff C. The knowledge complexity of interactive proof systems // SIAM J. Comput. / M. Sudan — SIAM, 1989. — Vol. 18, Iss. 1. — P. 186— 208.
- Goldreich O., Micali S., Wigderson A. How to Prove All NP Statements in Zero-Knowledge and a Methodology of Cryptographic Protocol Design: Extended Abstract // Advances in Cryptology — CRYPTO ’86: 6th Annual International Cryptology Conference, Santa Barbara, California, USA, 1986, Proceedings / A. M. Odlyzko — Berlin, Heidelberg, New York, NY, London [etc.]: Springer Berlin Heidelberg, 1987. — P. 171–185. — 490 p.
- Goldreich O. Zero-Knowledge Proofs for NP: Commitment Schemes // Foundations of Cryptography Basic Tools: Volume 1. — Cambrige University Press, 2001. — P. 224. — 372 p.







