В статье рассматривается история теоремы Пифагора и её применения на практике и в теории. Приведены различные примеры из жизненных задач.
Ключевые слова: математика, геометрия, Пифагор, теорема Пифагора, доказательство, решение задач.
Математика — это не только формулы, а это все, что нас окружает. В ней важно не только знать теоремы и аксиомы, но и понимать, чувствовать ее фундаментальные принципы. К одному из таких фундаментальных знаний можно отнести теорему Пифагора, с которой мы знакомимся еще в школе на уроках геометрии. Однако, как порой это бывает, учебная программа упускает красоту и изящество самой теоремы, чья роль намного важнее, чем нахождение сторон треугольника; теорема Пифагора находит неисчисляемое множество применений в науке и технике — невозможно переоценить ее значимость.
Начнем с того, что Пифагор — известнейший древнегреческий математик. С его именем связаны множество понятий и терминов.
Теорема Пифагора, а точнее, её принцип, пользовался интересом давно, даже до самого Пифагора, но, он обобщил этот принцип.
Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.
Теорема формулируется следующим образом: площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах. Открытие этого утверждения приписывают Пифагору. В школе теорема из себя представляет только следующее:
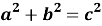
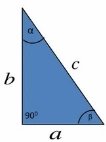
Рис. 1
Данная теорема в школе изучается только для применения в решении геометрических задач, но практическое применение тоже имеет место быть. Теорема Пифагора решает задачи с прямоугольными треугольниками, где нужно вычислить длины сторон. А на практике теорему могут применить при установки антенны для мобильной связи, например, ведь нужно правильно рассчитать высоту и радиус действия или в лесной промышленности: для потребностей строительства бревна распиливают на брус, при этом главная задача — получить как можно меньше отходов. Наименьшее число отходов будет тогда, когда брус имеет наибольший объем. Что же должно быть в сечении? Как видно из решения сечение должно быть квадратным, а теорема Пифагора и другие рассуждения позволяют сделать такой вывод.
В школе данную теорему изучают в 8 классе и не уделяют ей большое количество времени. Мы считаем, что теорема Пифагора легка для понимания, но для неё существует огромное кол-во применений. Её просто нужно увидеть в задаче и уметь выразить.
Доказательство теоремы Пифагора:

Рис. 2
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов (рис. 2).
Дано: ∆ABC, в котором ∠C = 90º.
Доказать: a 2 + b 2 = c 2 .
Пошаговое доказательство:
Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам: ∠ACB =∠CHA = 90º,
∠A — общий.
Также прямоугольная фигура ∆CBH подобна ∆ABC:
∠ACB =∠CHB = 90º,
∠B — общий.
Введем новые обозначения: BC = a, AC = b, AB = c.
Из подобия треугольников получим:

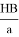


Значит a
2
= c
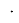

Сложим полученные равенства:
a
2
+ b
2
= c


a
2
+ b
2
= c

a
2
+ b
2
= c

a
2
+ b
2
= c

a 2 + b 2 = c 2
ч.т.д.

Рис. 3
С помощью этой теоремы решаются многие практические или олимпиадные задачи, например:
условие задачи на рис. 3.
Необходимо найти сторону CB.
Используем теорему Пифагора.
CB =
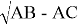
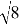
Ответ:
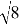
Пример 1: Кадету 8 класса требуется найти ширину пруда. Он нашел расстояние от точки R до точки P и Q, расположенных по разным сторонам пруда, как показано на рис. 4. И уточнил, что угол P прямой. Если пренебречь рассчётами кадета, какова длина пруда, отрезка PQ?
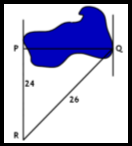
Рис. 4
Решение: если понять, что при соединении данных точек образуется прямоугольный треугольник, то эта задача слёгкостью решается теоремой Пифагора.
Дан катет треугольника и гопотенуза.
Применяя теормему составляем уравнение:
PR 2 + PQ 2 = QR 2
PQ 2 = QR 2 — PR 2
PQ =
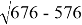

Ответ: длина пруда 10 м.
Задачи в курсе физики средней школы также требуют знания теоремы Пифагора
Пример 2: Биатлонист, стреляющий по мишени, делает поправку на ветер. Если ветер дует справа, а биатлонист стреляет по прямой, то пуля уйдёт влево. Чтобы попасть в цель, надо сдвинуть прицел вправо на расстояние смещения пули. Для них составлены специальные таблицы (на основе следствий из т. Пифагора). Биатлонист знает, на какой угол смещать прицел при известной скорости ветра.
Пример 3 : Каждому абоненту важна качественная сотовая связь. А качество зависит от высоты антенны мобильного оператора. Чтобы рассчитать, в каком радиусе можно принимать передачу. Для решения задачи можно применить теорему Пифагора.
Итак, можно сделать вывод, для человека, решающего олимпиадные задачи, мало знать только школьную программу, нужно углубляться в математику и глубже изучать каждую теорему, каждую закономерность, нужно улучшать понимание и умение находить в задачах красоту решения. И они заиграют новыми красками, потому что окажется, что теорема не только для треугольника, или она применяется не только для решения теоретических задач. А может быть, она задействована в разных разделах математики. Конкретно теорема Пифагора помогает во многом: решение школьных задач, олимпиадных работ и проста для понимания. К сожалению, на неё уделяют очень мало времени в школьной программе.
Литература:
- Мерзляк А. Г. Геометрия: 8 класс: учебник для учащихся общеобразовательных учреждений / А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. — М.: Вентана-Граф, 2020. — 208 с.
- Атанасян Л. С. Геометрия. 7–9 классы: учебник для учащихся общеобразовательных учреждений / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. — 20-е изд. — М.: Просвещение, 2010. — 384 с.







