Перед историками, археологами и искусствоведами часто встает задача оценки артефактов с точки зрения их художественной ценности, принадлежности к той или иной сакральной сфере. Важную роль при этом играет определение в изделиях принципов золотого сечения, которые широко использовались и используются для их гармонизации. Специалистам гуманитарного профиля иногда затруднительно применить для таких операций сложные математические методы. В данном материале опишем несложные, доступные и надежные способы установления наличия золотого сечения и других методов гармонизации художественных произведений и географических объектов.
Ключевые слова: артефакт, оценка художественной ценности, золотое сечение, пентаграмма, географические координаты, местоположение объектов по GPS, Делийская колонна, модуль изделия, размер кирпичей.
Historians, archaeologists and art historian often face the task of evaluating artifacts in terms of their artistic value, belonging to one or another sacred sphere. An important role is played by the definition of the principles of the golden section in products, which have been widely used and are being used to harmonize them. It is not easy for specialists in the humanities to apply complex mathematical methods for such operations. In this material, we will describe simple, affordable and reliable ways to establish the presence of the golden section and other methods for harmonizing works of art and geographical objects.
Keywords: artifact, artistic value assessment, golden ratio, pentagram, geographic coordinates, GPS location of objects, Delhi column, product module, brick size.
Прежде всего, обратимся к содержанию понятия «артефакт».
Артефа́кт (лат. artefactum от arte — искусственно + factus — сделанный) — в археологии — объект, подвергнутый в прошлом направленному механическому воздействию, обнаруженный в результате целенаправленных археологических раскопок или какого-либо единичного, иногда случайного события. Примерами артефактов являются каменные инструменты, ювелирные изделия, оружие, керамика, постройки и их детали, угли древнего костра, кости, имеющие следы воздействия человека и др. Артефакты изучаются археологами, которые производят раскопки археологических памятников, исследуют и публикуют находки и результаты раскопок и восстанавливают по этим данным историческое прошлое человечества. Также в русскоязычной литературе для названия артефактов использовались или используются такие эквивалентные термины:
а) вещественные источники. При использовании этого термина обычно подразумевается, что речь идёт об артефактах, которые не содержат каких-либо надписей. Артефакты, содержащие письмена, называют «письменными источниками»;
б) предметы материальной культуры. Здесь слово «культура» используется в том же смысле, что и в термине археологическая культура;
в) археологические памятники. Этот термин имеет более широкое значение, археологическими памятниками также называются более крупные объекты, такие как, например, древнее поселение в целом. Археологическими памятниками чаще всего называются особо ценные артефакты;
г) археологические находки. Среди них выделяются индивидуальные находки и массовые находки [11].
Перед историками, археологами и искусствоведами часто встает задача оценки артефактов с точки зрения их художественной ценности, принадлежности к той или иной сакральной сфере. Важную роль при этом играет определение в изделиях принципов золотого сечения, которые широко использовались и используются для их гармонизации. Специалистам гуманитарного профиля непросто применить для таких операций сложные математические методы. В данном материале опишем простые, доступные и надежные способы установления наличия золотого сечения и других методов гармонизации художественных произведений и географических объектов.
С помощью программы Microsoft PowerPoint можно произвести, пожалуй, самый лёгкий и доступный анализ наличия золотого сечения в артефакте. В художественных изделиях достаточно вписать в изображение пентаграмму (пятиконечную звезду). Ключевые точки рисунка должны совпасть с таковыми на геометрической фигуре. Мы расположили пентаграмму на одном из элементов наманганского сюзане. Этот рисунок представляет собой древо жизни. Как видно, пентаграмма полностью вписалась в изображение. Отдельные искажения произошли за счет неверного натяжения ткани.

По нашим наблюдениям, существовали и математические методы, которые через артефакты передавались с неолитического времени и сохранялись в их расположении и размерах. Использовались при этом цифры, отражающие золотое сечение φ — 1618 и 618; число π — 314; математическое выражение дюйма — 254; а также кратные армянской метрической меры кайла (ниппурского локтя) — 518. Кроме того, следует учитывать √2= 1414 (101); (в дальнейшем учитываются только модули чисел — автор), √3–1372 (7 3 ×2 2 ); √5 –2236=(43×13×2 2 ). Значительная часть известных нам метрических мер Евразии и Южной Америки основывается на этих цифрах.
В древности употреблялась разность указанных цифр и окружности — 360 и 720.
Таблица 1
|
360–314=46/23 |
360– 161=199 |
360–618 = –258=6×43 |
|
720–314=406 = 28×29 |
720–161=559=13×43 |
720–618 = 102= 6×17 |
|
360–254=106/53 |
360–127=233чф |
360–518 = –158/79 |
|
720–254=466/233чф |
720–127=593 |
720–202/101 |
|
360–141=219/73 |
360–137= 223 = 11× 202,7 |
360–64= 296 = 8х37 |
|
720–141= 579=3×193 |
720–137=583 = 11×53 |
720–64=656= 41×2 3 |
Следует также учитывать цифры 97, 137, 131 и 173/187.
Ниже приведем таблицу чисел Фибоначчи и Люка, отражающую золотое сечение, с их кратными. Многие величины, употребляемые в древности, сводятся к этим цифрам. В дальнейшем такие числа будет обозначать «чф», кратные этим числам «кчф».
Таблица 2
|
Единицы |
1 |
2 |
3 |
4 |
5 |
7 |
8 |
9 |
|
Десятки |
11 |
13 |
15 |
17 |
18 |
19 |
21 |
23 |
|
27 |
29 |
34 |
41 |
47 |
55 |
61 |
89 |
|
|
Сотни |
107 |
123 |
141 |
144 |
161 |
199 |
233 |
281 |
|
305 |
321 |
322 |
323 |
329 |
377 |
451 |
610 |
|
|
843 |
963 |
987 |
||||||
|
Тысячи |
1353 |
1597 |
2207 |
2255 |
2584 |
2741 |
2889 |
4181 |
|
5778 |
6765 |
10964 |
15217 |
17711 |
Каждое из этих чисел отражает важнейшие явления природы, но в задачу данного материала не входит их анализ.
Что касается определения географических координат сакральных сооружений, которые, начиная с так называемых неолитических «хенджей» по новейшие храмы включительно, то они строились и строятся на местах, географические координаты которых кратны 37.
Так как географические координаты представляют собой матрицу из шести элементов, достаточно произвести все возможные операции на сложение, чтобы убедиться, что в результате вычислений содержатся числа 37, 74, 111, 148, 185, 222, 269, 296 или их обратные от 360 и 720.
Возьмем сооружения на разных континентах Земли. К примеру, Голоринг — древнее деревянное сооружение вблизи Кобленца в Германии 1200–800 гг. до н. э. Его координаты оформим в виде таблицы.
Таблица 3
|
50. 20. 21=91 07 . 26 . 23 = 56 57. 46. 44.=146 |
50+7+21+23=101; 50+26+21=97; 20+26+23=69; 20+21+23=64; 21+26+20+7=74; |
360–101=259=7х37; 360–97=263=13х202,3; 360–69=291=3х97; 360–64= 296 = 8х37; 74=2х37 |
Рассчитаем самый западный из майяских храмов Северной Америки Комалькалько в мексиканском штате Табаско.
Таблица 4
|
18. 16. 45= 79 93 . 12 . 04 = 109 111.28. 49.= 188 |
18+93=111; 111+ 16 = 127; 111+12=123чф; 111+45=156; 28+93=121; 49+18=67; 49+12=61; 79+12=97; 93+4=97; 93+16+4=113; 12+45=57; 18+16+4=34чф; |
111=3х37; 127х2=314 (π); 123чф; 156=12х13чф; 121=112чф; Мера объёма в России XVIII века малая четь 0,427 см3; 427–360=67; 61чф; 360–97=263=13х202,3; 360–97=263=13х202,3; 133=7х1614 φ; 360–57=303=3х101; 360–101=259=7х37 34чф |
Рассмотрим курган Безымянный в Черниговской области X века. Возьмем только характерные результаты
Таблица 5
|
51. 29. 14= 94 31 . 17 . 38 = 86 82. 46. 52.= 180 2х180 =360; |
51+31+29=111; 51+29+14+17=111; 94=2х47; 51+31+46=128=2х64; 29+17=51=97; 14+38+17=69; 31+17+38+51=137; 51+17=68=2х34; 51+38=89; |
111=3х37; 111=3х37; 47чф2х180 =360; 360–64= 296 = 8х372х180 =360; 360–97=263=13х202,32х180 =360; 360–69=291=3х972х180 =360; 720–137=583=11х532х180 =360; 34чф 2х180 =360; 89чф |
Следовательно, курган Безымянный можно отнести к сакральным сооружениям.
В труде Бируни «Геодезия» координаты городов строятся по тому же принципу [1, 370].
Автор не выяснил причину того, почему все сакральные сооружения мира имеют координаты, кратные 37, причем именно в системе географических координат с нулевым меридианом от Гринвича. Возможно, это связано с икосаэдро-додекаэдрической структуры Земли (сокращенно ИДСЗ ) [7, 30]. Но это обстоятельство поможет определить сакральность сооружений при археологических раскопках, тем более в настоящее время легко найти местоположение объектов по GPS.
Наличествует ли золотое сечение в артефактах, поддающихся измерению, можно узнать в том случае, если объект не поврежден или его габариты можно достоверно установить. В таком случае нужно величину разделить на 8 частей и выделить 5 из них: на объекте эти пункты будут так или иначе обозначены. Более сложный способ: разделить величину на 161 или помножить на 618.
К примеру, характеристики так называемой Делийской колонны следующие: высота –7,21 м; диаметр внизу — 0,485 м; диаметр вверху — 0,223 м. Чтобы вычисления были правильными, надо восстановить первоначальную высоту колонны. Абу Рейхан Аль-Беруни писал о колонне:
«… арабами был найден железный столб высотой в 70 локтей. Хишам ибн-Амир приказал откопать его до основания, и при этом было обнаружено, что столб был вкопан ещё на 30 локтей в землю» [5, 52–53].
Если 721м. составляют 70 локтей, то 30 локтей составят 309 м. В результате сложения получаем 1029 метров или 3х7 3 . Золотое сечение высоты колонны составляет 1029/1618=0,63597; 635/5=127.
Диаметр внизу 485 = 5х97.
Диаметр вверху — 223 или 360–137.
Следовательно, индийские металлурги и инженеры V века учитывали принципы гармонизации в своём изделии.
Наши предшественники учитывали также длину и ширину станковых произведений. Проанализируем размеры иконы Рублева «Троица» («Гостеприимство Авраама») XV века. Они составляют 142 х 114 см.

Источник: [10]
При умножении этих чисел получаем результат 16188 — числовое выражение золотого сечения φ.
Обратимся к гармонизации в ювелирных изделиях. Такие изделия, как кашгарские серьги и подвески представляют собой сложные конструкции, имея в основе символы стихий, различного рода геометрические фигуры, в том числе и пентаграмму, и, возможно, указывают на соотношение размеров планет Солнечной системы.
В данном случае рассмотрим подвеску и применим к ней модульный анализ, который легко произвести с помощью Microsoft PowerPoint. На рисунке видно, что отдельные модули вписываются в более крупные без остатка, следовательно, создатели изделия гармонизировали его.


Рассмотрим национальную одежду. Покрой такого предмета, как национальные штаны не менялся столетиями. В труде Н. Садиковой «Ўзбек миллий кийимлар» [6,122] помещено лекало с указанием размеров предмета. Просчитаем их.
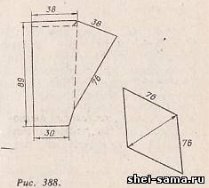
Сложим цифры, обозначающие их размеры: 89чф+38+30+ 38+76. Получаем ряд: 127, 157, 195, 271. Как мы уже знаем, 127 — ½ дюйма, 157–1/2 π, 195–15х13чф, 360–291=97.
Половина вставного клина представляет собой равнобедренный треугольник со сторонами 76 см., углом вершины 40 градусов и двумя углами по 70 градусов. Если подойти формально и просчитать цифры 76,40, 70, получится следующее:
360–(40+76) = 244=4х61чф; 360–(70+76)=214=2х107кчф.
В древности учитывались размеры всех элементов архитектурных сооружений, в том числе и кирпичей.
Таблица 6
|
№ |
Страна, время |
Размер кирпича |
Расчеты |
|
1 |
Древний Рим |
плинфа 50 х 55 х 4,5 см |
500 х 550 х 45=1095=15х73; 50045=455=5х91=35х13; 550–43=505=5х101; 360–101=259=7х37 [4] |
|
2 |
Россия Московский Кремль |
556x286x156 мм |
556x286x156=998 360–286=74=2х37 [9] |
|
3 |
Узбекистан Кашкадарьинская область. Согд, 5–6 век, Аул-тепе |
41х25х8 см |
41х25х8=74=2х37 [2, 52] |
|
4 |
Россия. Кирпич Аристотеля Фьораванти (1475–1479 гг.) |
189х89х67 |
189х89х67=345=3х69; 189+67=256 / 4х64; 189+89=278=2х139; 89+67=156 = 12х13; 189:7=27 [8, 946–950] |
|
5 |
Узбекистан, Наманганская область. Закладной кирпич в мечети, древний Ахсикент, XV век |
316+182+42 = 540 |
316+182+42 = 540 316–182=134 (2х67). 316+182= 498 (2х249; 3х83) 316+ 42= 358(2х179) 316–42 = 274 (2х137) [3] |
|
6 |
Германия «Рейх формат» 1872 |
250х120х65мм |
250х120х65=435=5х87; 250+120=370; 250+65=315=15х21чф [12] |
|
7 |
США, кирпич NORMAN (В США 11 наиболее широко производимых размеров кирпичей. Все они содержат ЧФ. Мы приводим наиболее яркий пример — автор) |
92 x 57 x 295 |
92 x 57 x 295=444=12х37 |
Применяя вышеуказанные методы, можно без затруднений определить, содержатся ли гармонизирующие принципы и золотое сечение в артефакте.
Литература:
- Бируни А. Р. Избранные произведения. — Том 3. — Геодезия. — Ташкент: 1966. — С. 370.
- Кабанов С.К К изучению аграрного строя Согда в 5–6 века. — М. 1965. — С. 52.
- Кирпич в Германии // http://kirpichdelo.ru/germany.htm.
- Курицын Е. М. История кирпича и кирпичная коллекция// https://ist-konkurs.ru/raboty/2012/772-historykirpi4
- Мезенин, Н. А. Железная колонна в Дели// Занимательно о железе. — М.: Металлургия, 1972. — С. 52–53.
- Садикова Н. «Ўзбек миллий кийимлар» XIX–XX аср. — Т., 2002. — С. 122.
- Соколова Л. М. Золотое сечение и сакральная геодезия // Актуальные вопросы общества. — Пенза, 2022. — С. 30.
- Соколова, Л. М. Применение принципов золотого сечения в размерах кирпича древнего Ахсикента // Молодой ученый. — 2015. — № 9 (89). — С. 946–950.
- http://moscowstate.ru/proizvodstvo-kirpicha-i-stroitelstvo-v-moskovskom-gosudarstve-v-xvi-hvii-vekah/
- https://ru.m.wikipedia.org/wiki/ Google_Art_Project.jpg
- https://ru.wikipedia.org/wiki
- https://vse-otoplenie.ru/razmer-oblicovocnogo-kirpica-formaty-standart-i-evro







