Целью настоящей статьи является вывод некоторых формул для определения длин частей диагоналей произвольных выпуклых четырехугольников. Эти части получаются при пересечении диагоналей данного четырехугольника.
В статье получены некоторые интересные результаты, которые по мнению авторов ранее не были опубликованы.
Сначала рассмотрим вписанный в окружность выпуклых четырехугольник.
На рисунке показан четырехугольник ABCD, где N является точкой пересечения диагоналей AB и CD.
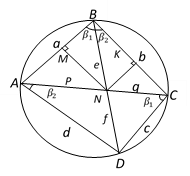
Рис. 1
Предположим, что в данном четырехугольнике
AB = a, BC = b, CD = c, AD = d, BD =
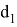
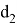
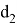
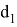
∠ABN = ∠ACD =
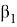
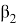
Как известно для четырехугольников вписанных в окружность, существует теорема Птоломея
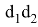
и формула Р.Симпсона, которая имеет вид [1,2,3]:
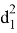
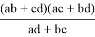
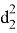
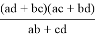

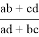
Зададимся целью нахождения формул для определения длин частей диагоналей e, f, p и q . Тоесть постараемся вывести формулы, выражающие эти длины через стороны a,b,c,d четырехугольника ABCD.
Предположим, что

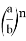

где
n
некоторое положительное действительное число,
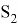
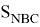
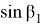
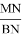
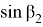
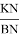
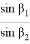
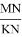

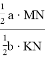
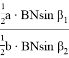
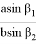
Откуда получаем
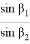


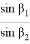

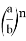
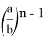
С другой стороны используя теорему синусов для треугольника ACD, можно написать следующие формулы:
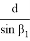
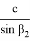
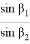

Используя формулы (4) и (5), получаем

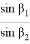
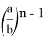

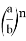
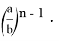
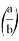
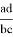
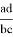

Следует отметить, что формулу (6) можно получить другим способом. Как можно увидеть из рис.1 следующие треугольники подобны:
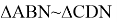


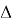
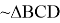


Умножая, соответственно правые и левые части уравнений (7) и (8) получаем
pcfb
=
afqd
=>
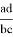





А теперь, преобразуя формулу (6), получим искомые формулы:

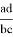

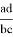
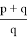
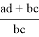

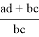
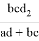
Подставляя вместо
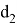
q = bc
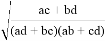
Поступая аналогичным образом, можно получить и все другие необходимые формулы:

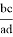

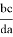
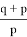
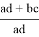

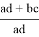
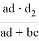
или
p = ad
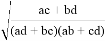
Выполняя те же действия, можно также получить формулу

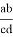
Тогда

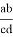
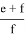
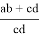
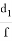
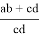
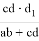
или
f
=
cd
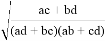
Таким же образом получаем

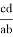
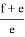
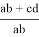
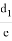
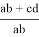
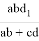
или
e
=
ab
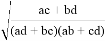
Покажем два примера применения данных формул.
Пример 1
. Предположим, дается четырехугольник со сторонами:
a=3, b=5,c=7,d=7.
Используя формулы (10), (12), (15), (17), можно получить значения
q
=
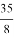
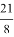
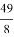
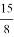
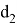
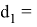
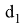
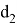
Пример 2. Атеперь предположим, нам дается трапеция ABCD со сторонами AB=a=5, BC=b=2, CD=c=5, AD=d=8 (рис.2). Нужно найти отрезки AO, OC.
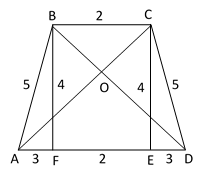
Рис. 2
Сначала решим эту задачу традиционным способом. Проведем перпендикуляры BF и CE к основанию AD.
Тогда FE=2, AF=ED. Используя теорему Пифагора, получаем BF=CE=4 и AC =
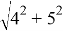
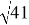
Далее из подобия треугольников
AOD
и
BOC
имеем
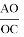

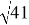
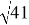
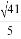
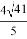
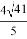
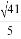
Используя далее полученные нами формулы получаем:
AO = p= ad
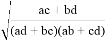
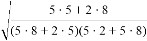
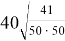
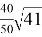
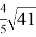
OC = q = bc
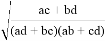
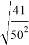
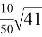
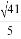
Как видим, получается один и тот же результат. Следует отметить что так как вокруг любой равнобочной трапеции можно описать окружность, то мы можем применить эти формулы.
Таким образом, нами здесь получены формулы, позволяющие выразить части диагоналей полученных делением их точкой пересечения через стороны данного выпуклого четырехугольника вписанной в окружность.
А теперь определим длины частей диагоналей произвольного выпуклого четырехугольника
ABCD
с
теми же обозначениями сторон, диагоналей и их частей. Дополнение ко всему пусть ∠A=
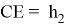
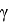
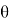
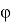
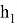
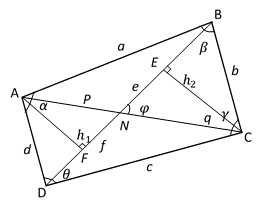
Рис. 3
Предположим, что даны стороны
a, b, c, d
и углы
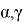
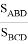
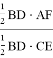
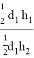

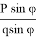

В таком случае,
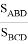

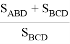
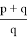

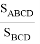

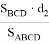
Здесь предстоит определить длину
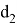
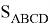
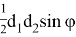
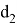
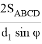
Здесь
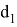
BD
=
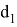
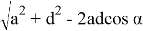
Покажем, что зная
a, b, c, d,
можно определить
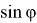
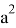
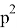
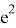
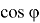
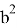
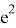
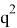
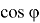
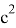
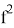
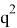
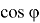
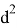
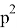
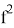
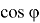
Откуда получаем:
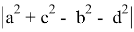
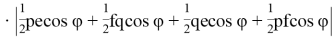
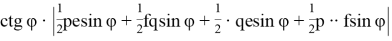
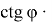
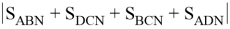
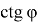
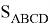
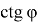
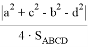
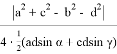
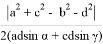
Как известно,
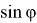
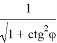
Далее, используя (19), (20), (22) в (18) получаем:
q
=
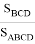
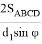
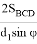
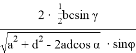
=>
q
=
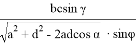
Далее, поступая аналогичным образом, имеем:
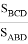

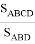

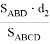
Используя (19) и (20), получаем:
p
=
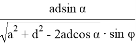
А теперь, получим такие же формулы для f и e:
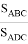

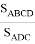
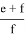
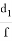
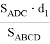
где
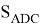

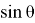
Для определения
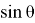
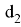

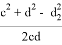
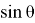
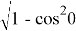
Учитывая это, f можно определить по формуле
f =
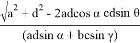
Для определения значения длины e поступаем аналогичным образом:
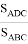

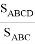
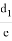
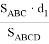
где
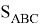

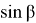
Таким же образом, используя формулу (19), можно определить:
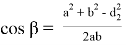
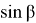
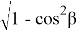
Учитывая сказанное, для определения значения длины e можно написать формулу в виде:
e =
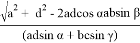
Таким образом, зная стороны
a, b, c, d
и углы
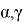

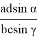
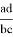

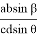
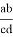
так как
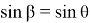
То есть получаем формулы (6) и (13), преобразуя которые можно получить необходимые формулы для выпуклых четырехугольника вписанных в окружность.
Литература:
- М. А. Горелов. Формула и содержание, Матем. просв., 2020, выпуск 26, 83–110
- И. Г. Малышев. Геометрия вписанных и описанных четырехугольников. Учебное пособие. Нижний Новгород 2019, 66 стр.
- Josefsson. M. The Area of a Bicentric Quadrilateral/ M.Josefsson// Forum Geometriconum — 2011. — Vol. 11. P. 155–164.
- C. A. Bretchneider. Untersuchung der trigonometrischen Relationen des geradlinigen Viereckes. Archiv der Mathematik und Physik, 2, s. 225–261.







