Фуллерены — одни из последних модификаций углерода, имеющие замкнутое строение и являющиеся весьма перспективными соединениями, обладающие сверхтвердыми, ферромагнитными, жидкокристаллическими, полупроводниковыми и др. ценными свойствами наноматериалов, обусловленных неклассическим атомным строением [1].
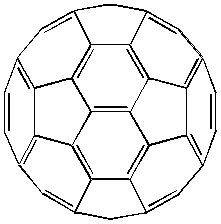
Рис. 1. Модель молекулы фуллерена С60.
В настоящее время предложена модельная оценка энергии образования молекул в ряду полиаддуктов фуллеренов неклассического строения, позволяющая количественно сравнивать искажения каркаса в этих соединениях [2].
С60 фуллерен состоит из 12 пентагонов и 20 гексагонов. Теоретически возможно 12500 вариантов расположения двойных и ординарных связей. Но наиболее стабильный изомер (рис.1) имеет структуру усеченного икосаэдра, в которой отсутствуют двойные связи в пентагонах, получивший название «Бакминстерфуллерен» в честь известного архитектора по имени R. Buckminster Fuller, создавшего сооружения, куполообразный каркас, который сконструирован из пентагонов и гексагонов [3].
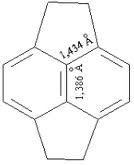
Исходя из очень сложного и длинного названия молекулы фуллерена С60 по химической номенкулатуре (гентриаконтацикло- [29.29.0.02,14.03,12.04,59.05,10.06,58.07,55.08,53.09,21.011,20.013,18.015,30.016,28.017,25.019,24.022,52.023,50.026,49.027,47.029,45.032,44.033,60.034,57.035,43.036,56.037,41.038,54.039,51.040,48.042,46] — гексаконта — 1, 3, 5 (10), 6, 8, 11, 13 (18), 14, 16, 19, 21, 23, 25, 27, 29 (45), 30, 32 (44), 33, 35(43), 36, 38(54), 39(51), 40(48), 41, 46, 49, 52, 55, 57, 59-триаконтаен), такие каркасные соединения углерода С60 и выше получили тривиальное название «фуллерены» и обозначаются Сn, где n=60, 70, 80 и т. д. с четными значениями индексов. В углеродном каркасе атомы углерода С характеризуются sp2-гибридизацией и валентная связь С4 реализуется за счет р — связей между углеродными атомами. Эмпирически установлено, что наиболее стабильными являются те фуллерены, в которых пентагоны не касаются друг друга и окружены пятью гексагонами. В отличие от бензола, гексагоны в фуллеренах имеют два типа связей: со значениями длин связей 1,386 Å и 1,434 Å, из которых короткие связи относятся к граням соседствующих шестиугольников, а длинные расположены между соседствующими пяти– и шестигранниками (рисунок 2).
Рис. 2.
Таким образом, фуллерен С60 имеет большое число эквивалентных реакционных центров и в связи с этим — сложных изомерных составов продуктов реакции с их участием (реакции гидрирования и галоидирования). Показано, что в каркасе С70 наиболее реакционно способной является связь между атомами углерода пентагонов и гексагонов, а затем связи между гексагонами, играющие большую роль в реакциях региоспецифического присоединения по π–связям [4]. Поэтому полученные полигидро– и полигалогенфуллерены С70 имеют только четное количество присоединенных водородов и галогенов.
Все эти особенности фуллереновых кластеров выдвигают задачу определения количества одинарных и двойных связей в продуктах присоединительных реакций в составляющих их изомерах.
Наиболее достаточным при этом является метод расчета числа связей в фуллеренах С60, С70, С80, С90, С100 и в продуктах их присоединительных реакций.
Как отмечалось ранее, построение графической формулы сложных химических соединений требует достаточно большого времени и создает определенные трудности [5]. А поскольку молекулы фуллеренов имеют сферическое строение и включают в себя большое число атомов, то подсчет числа связей усложняется, даже, если использовать трехмерные химические модели. Следовательно, было бы более удобно вычислять число связей в таких больших и сложных молекулах, как фуллерены, математическим путем.
Из
формулы
![]() ,
предложенной нами [6]
для расчета химических связей соединений без применения графических
формул возможно вывести математическую формулу для вычисления числа
связей в молекуле фуллерена:
,
предложенной нами [6]
для расчета химических связей соединений без применения графических
формул возможно вывести математическую формулу для вычисления числа
связей в молекуле фуллерена:
где, А — общее число химических связей,
a1a2 — количество атомов различных элементов,
e1e2 — число валентных электронов, затраченных этими элементами для образования химической связи.
Поскольку
молекула фуллерена состоит только из атомов углерода, и на
образование химической связи затрачивается 4 валентных электрона, то
исходя из вышеуказанного, преобразуем формулу
![]() в
формулу
в
формулу
![]() ,
согласно которой можно рассчитать число связей в фуллеренах Сn:
,
согласно которой можно рассчитать число связей в фуллеренах Сn:
Рассмотрим
подсчет числа химических связей в молекулах фуллеренов С60
и С70.
Количество атомов углерода, входящего в состав молекулы равно 60
и 70 соответственно и каждый атом углерода в обеих
молекулах
потратил
на образование химической связи 4 валентных электрона. Отсюда, общее
число связей в С60
и С70
будет равны
![]() и
и
![]() .
.
Таким образом, становится возможным за короткое время и с большой точностью подсчитать число связей без использования графических формул.
Как известно, в молекулах фуллеренов большинство реакций идет по двойным связям, следовательно, подсчет числа двойных связей составляет основной интерес.
Исследования, проведенные нами по данному вопросу дали ожидаемый результат. Путем математических подсчетов была предложена формула, удовлетворяющая подсчет числа двойных связей в молекулах фуллеренов.
Для этого в начале мы вывели формулу для расчета числа одинарных связей в фуллеренах:
где n1 — число пентагонов фуллерена, а n2 — число гексагонов, входящих в молекулу фуллерена, где числа 5 и 6 указывают на количество сторон в пентагоне и гексагоне соответственно.
Применим эту формулу для молекулы фуллерена С70: известно, что количество пентагонов в фуллеренах, вне зависимости от числа атомов, входящих в молекулу равно 12, а гексагонов равно 25. Отсюда,
Следовательно, количество одинарных связей в молекуле С70 равно 105. Отсюда можно вывести, что разность общего числа связей в фуллерене С70 и числа одинарных связей дает число двойных связей.
Тогда общая формула для расчета количества двойных связей в молекуле фуллерена примет следующий вид:
Таким
образом, зная количество общего числа связей и числа одинарных
связей в молекуле, можно с легкостью вычислить число
двойных связей. Например, число общих связей в молекуле С70
равно 140, а число одинарных связей — 105. Тогда,
согласно формуле
![]() вычислим:
вычислим:
Экспериментальная часть:
П![]() остроение
моделей молекул фуллеренов выполняется с помощью цветного
картона, из которого вырезаются равносторонние пятиугольники
(пентагоны) и шестиугольники (гексагоны), имеющие одинаковую
длину сторон. Для легкой визуализации моделей пятиугольники
и шестиугольники вырезают из картона двух разных цветов.
Количество пятиугольников у всех моделей молекул фуллеренов
одинаково и равно 12, а количество шестиугольников
различается в зависимости от количества атомов, входящих
в молекулу фуллерена, модель которой строится. Таким образом,
у молекулы, имеющей количество атомов равным 60 количество
шестиугольников равно 20; 70 соответственно 25, 80–30; 90–35
и 100–40.
остроение
моделей молекул фуллеренов выполняется с помощью цветного
картона, из которого вырезаются равносторонние пятиугольники
(пентагоны) и шестиугольники (гексагоны), имеющие одинаковую
длину сторон. Для легкой визуализации моделей пятиугольники
и шестиугольники вырезают из картона двух разных цветов.
Количество пятиугольников у всех моделей молекул фуллеренов
одинаково и равно 12, а количество шестиугольников
различается в зависимости от количества атомов, входящих
в молекулу фуллерена, модель которой строится. Таким образом,
у молекулы, имеющей количество атомов равным 60 количество
шестиугольников равно 20; 70 соответственно 25, 80–30; 90–35
и 100–40.
Рис. 3.
Построение начинается с пятиугольника, который соединяют клейкой лентой по сторонам с пятью шестиугольниками, в результате чего получается фигура на рис. 3. Далее, к каждому из пяти свободных углов, образованными двумя шестиугольниками, присоединяют пятиугольники и дальше оставшиеся шестиугольники. Таким образом, каждый пентагон в построенной модели молекулы не зависимо от числа атомов, входящих в нее, окружен пятью гексагонами, как это указано на рис. 3. Остальные шестиугольники располагаются между ними. Именно поэтому с модели молекул, имеющих более 60 атомов, представляют собой вытянутую форму (рис.4).
Рис. 2. Модели молекул фуллеренов С60, С70, С80, С90 и С100.
Литература:
П. А. Трошин, Р. Н. Любовская «Успехи химии» 77, № 10, (2008)
Автореферат диссертации на соискание ученой степени доктора химических наук Словохотова Ю. Л. «Атомное строение и особенности кристаллохимии новых производных фуллеренов» 2008.
Гусев А. И. «Наноматериалы, наноструктуры, нанотехнологии». — М.: Физматлит, 2007. — 416 с.
П. А. Трошин, Р. Н. Любовская «Обзорный журнал по химии» т. 77, № 10, 2008 год, стр. 97.
Салахов М. С., Багманов Б. Т., Аббасов З. С. «Математическое выражение количества связей в химических соединениях» Актуальные проблемы гуманитарных и естественных наук № 8 август 2010 том 1.
Салахов М. С., Аббасов В. М., Багманов Б. Т., Аббасов З. С. «Математическое выражение числа связей в химических соединениях», «Химия в школе», 2 (22) 2008, с 70–75.