Задачи о дифракции волн упругих телах, содержащих дефекты, представляют значительный интерес. В данной статье описан метод, связанный с применением аппарата специальных функций Матье и она является продолжением работы [1, с. 121]. Он применим для широкого класса задач, в которых можно считать, что дефект имеет эллиптическую форму.
Как известно, цилиндрические эллиптические координаты вводятся с помощью соотношений
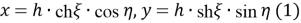
Координаты линиями
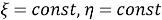
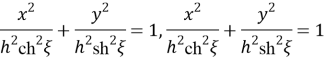
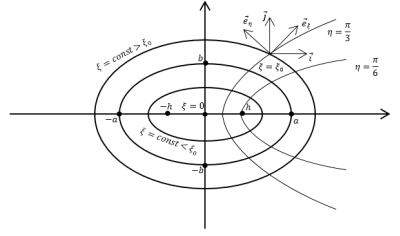
Рис. 1. Семейство координатных линий
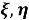
Параметр
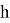
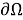
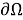
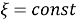
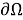
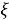
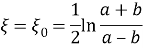
Таким образом, эллипс
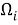
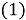
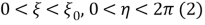
Отметим предельные случаи: если
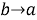
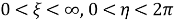
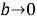
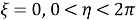
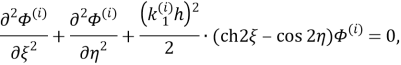
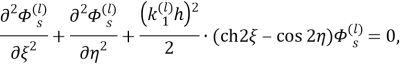
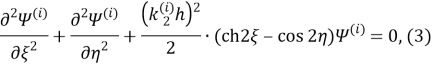
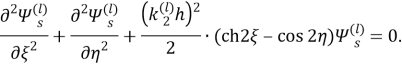
Преобразуем к эллиптическом координатам известные потенциалы
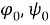
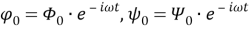
Здесь
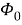
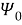
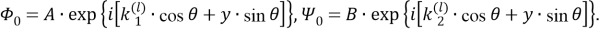
Функции
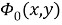
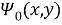
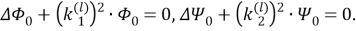
Согласно
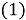
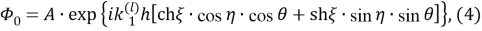
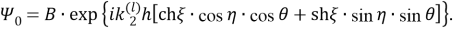
Перейдем к формулировке граничных условий, вытекающих из
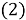
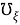
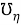
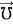
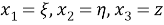
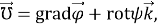
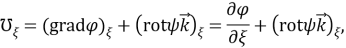
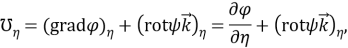
Контрвариантные компоненты
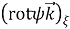
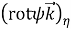
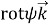
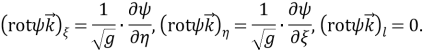
Здесь
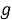
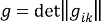
Для выбранной системы координат имеем [3, с. 123]:
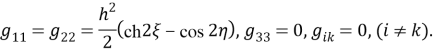
Таким образом
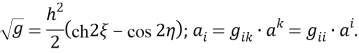
Отсюда вытекает, что
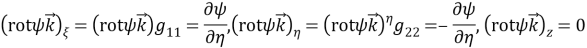
следовательно
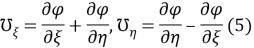
Искомый вектор перемещения выражается через
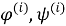
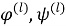
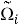
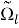
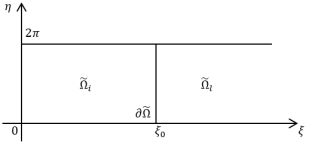
Рис. 2. Образы
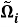
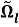
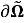
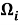
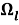
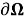
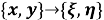
Используя
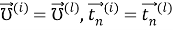
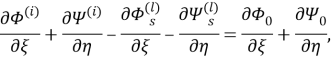
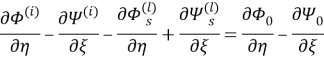
при
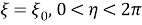
Рассмотрим вектор напряжения
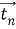
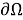
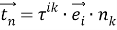
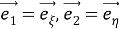
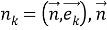
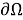
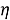
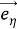
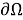
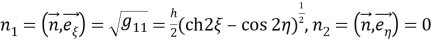
Следовательно
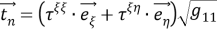
Это приводит к следующим условиям
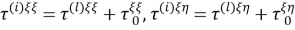
при
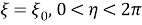
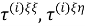
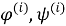
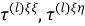
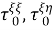
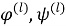
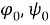
Таким образом, рассматриваемая краевая задача состоит в нахождении функций
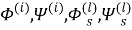
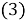
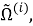
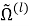
Кроме того должны выполнены условия периодичности
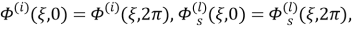
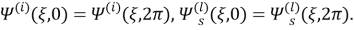
и условия ограниченности искомых функций при
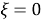
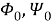
Литература:
- Международный научный журнал «Символ науки» (ISSN 2410–700X) № 11–2/2023.
- Бейтмин Г., Эрдейи А. Высшие транцендентные функции. Функции Ляме и Матье. -Москва: Наука, 1967.
- Блох В. И. Теория упругости. -Харьков: издательство ХГУ, 1964.







