В статье рассматривается применение нечетких тензорных моделей в анализе технико-экономической информации. Нечеткая логика и тензорные модели представляют собой эффективный инструмент для работы с многомерными и нечеткими данными, что делает их особенно полезными в экономике и управлении. Рассмотрены преимущества и примеры применения нечетких тензорных моделей, такие как прогнозирование спроса на продукцию, анализ эффективности производственных процессов и принятие решений о распределении ресурсов. В заключении подчеркнута перспективность использования нечетких тензорных моделей в анализе данных для принятия обоснованных и эффективных решений.
Ключевые слова : нечеткая логика, тензорные модели, анализ данных, технико-экономическая информация, прогнозирование, оптимизация.
- Введение
Анализ технико-экономической информации играет ключевую роль в современном бизнесе и управлении. Однако, в контексте динамично меняющейся экономической среды, традиционные методы анализа, основанные на точных числовых данных, могут оказаться недостаточно гибкими для учета неопределенности и размытости, характерных для многих экономических явлений.
В последние годы нечеткая логика и тензорные модели привлекают все большее внимание исследователей и практиков в области анализа данных. Нечеткие тензорные модели представляют собой эффективный инструмент для работы с многомерными данными, учитывающий не только значения параметров, но и их взаимосвязи.
Целью данной статьи является рассмотрение применения нечетких тензорных моделей в анализе технико-экономической информации. Мы рассмотрим основы нечеткой логики и тензорных моделей, их преимущества по сравнению с традиционными методами анализа данных, а также конкретные примеры применения в различных сферах бизнеса и управления. [3]
- Основы нечеткой логики и тензорных моделей
Нечеткая логика и тензорные модели представляют собой два важных аспекта современного анализа данных, особенно в контексте анализа технико-экономической информации. Нечеткая логика позволяет оперировать нечеткими понятиями и значениями, что позволяет учитывать неопределенность и размытость данных. Тензорные модели, в свою очередь, позволяют работать с многомерными данными, учитывая взаимосвязи между различными параметрами. [1]

где
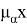
Нечеткая логика основывается на идее принадлежности элемента к множеству с определенной степенью принадлежности, в отличие от классической бинарной логики, где элемент либо принадлежит множеству, либо не принадлежит. Такой подход позволяет более гибко моделировать реальные ситуации, где понятия не всегда могут быть однозначно определены. [2]
Тензоры представляют собой обобщение матриц на более высокие размерности и позволяют компактно хранить и анализировать многомерные данные. Они нашли широкое применение в различных областях, таких как обработка изображений и сигналов, где необходимо учитывать не только отдельные значения, но и их структуру и взаимосвязи. [3]
Нечеткие тензорные модели сочетают в себе преимущества нечеткой логики и тензорного анализа, позволяя анализировать сложные структуры данных, учитывая их неопределенность и размытость. Такие модели могут быть эффективно применены в анализе технико-экономической информации для прогнозирования, оптимизации и принятия решений в условиях неопределенности и разнообразия параметров. [4]
- Применение нечетких тензорных моделей в анализе технико-экономической информации
Анализ технико-экономической информации включает в себя оценку производственных процессов, прогнозирование спроса на продукцию, оптимизацию ресурсов и множество других задач, которые требуют учета множества параметров и их взаимосвязей. В контексте такой сложной и разнообразной информации нечеткие тензорные модели представляют собой мощный инструмент для анализа и принятия решений.
Для прогнозирования спроса на продукцию с использованием нечетких тензорных моделей можно воспользоваться следующей формулой для оценки принадлежности элемента к категории:
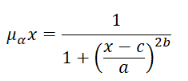
где:
— x — значение параметра (например, цена, рекламный бюджет и т. д.);
— c — центр категории (например, оптимальная цена);
— a — ширина категории (чем меньше, тем более резким будет переход между категориями);
— b — параметр, определяющий «крутизну» перехода между категориями.
Такая функция принадлежности может быть использована для определения степени принадлежности каждого значения параметра к каждой категории спроса (например, низкий, средний, высокий).
Для прогнозирования спроса можно использовать нечеткие правила, которые определяют связи между значениями различных параметров и уровнями спроса. Например, если цена низкая и рекламный бюджет высокий, то спрос высокий.
Далее, с помощью операций тензорного умножения и агрегации можно объединить все нечеткие правила и определить общую степень принадлежности каждого сценария к различным уровням спроса.
Преимущества использования нечетких тензорных моделей в анализе технико-экономической информации огромны. Во-первых, они позволяют учитывать неопределенность и размытость данных, что особенно важно при работе с реальными экономическими данными, где информация может быть неполной или недостоверной. Во-вторых, эти модели способны обрабатывать многомерные данные, учитывая не только отдельные параметры, но и их взаимосвязи, что позволяет более точно моделировать сложные экономические процессы. [10]
- Конкретные примеры применения нечетких тензорных моделей
Применение нечетких тензорных моделей в анализе технико-экономической информации может быть иллюстрировано рядом конкретных задач и сценариев, где эти модели проявляют свою эффективность. Рассмотрим несколько примеров:
Прогнозирование спроса на продукцию: Представим, что компания занимается производством электроники и планирует выпуск новой модели смартфона. Нечеткая тензорная модель может использоваться для анализа исторических данных о продажах, маркетинговых акциях, экономических показателях и других факторах, чтобы предсказать спрос на новую модель смартфона в различных сценариях. Для прогнозирования спроса на продукцию с использованием нечетких тензорных моделей можно применить методы нечеткой логики и тензорного анализа. Один из подходов основан на использовании нечетких правил и нечетких тензоров.
Например, есть нечеткие правила вида «Если X1 — высокий, X2 — средний, X3 — низкий, то спрос — высокий». Такие правила можно записать в виде тензора, где каждому правилу соответствует элемент тензора.
Далее, можно представить значения параметров (X1, X2, X3) в виде нечетких чисел и вычислить степень принадлежности каждому из них к определенной категории (высокий, средний, низкий).
С помощью операций тензорного умножения и агрегации можно объединить все нечеткие правила и определить общую степень принадлежности каждого сценария к различным уровням спроса. [4]
Анализ эффективности производственных процессов: Предположим, что компания занимается производством автомобилей и стремится оптимизировать производственные процессы для улучшения эффективности.
Пусть
Для
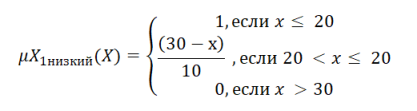


Для
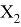
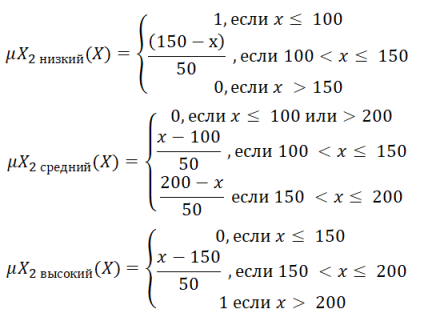
Для Y

Тогда, можно определить степень принадлежности каждого фактора к определенной категории (например, низкая, средняя, высокая) с помощью функции принадлежности нечеткой логики.
После этого, можно использовать нечеткие правила для определения связей между значениями факторов и уровнем эффективности производства. Например, «если скорость высокая и качество среднее, то эффективность высокая».
Далее, с помощью тензорного умножения и агрегации можно объединить все нечеткие правила и определить общую степень принадлежности каждого сценария к различным уровням эффективности производства.
Таким образом, нечеткие тензорные модели позволяют учитывать многомерность данных и сложные взаимосвязи между различными параметрами при анализе эффективности производственных процессов.
Нечеткие тензорные модели могут быть использованы для анализа данных о производственных операциях, использовании ресурсов, качестве продукции и других параметрах, чтобы выявить узкие места и оптимизировать производственные процессы. [8]
Принятие решений о распределении ресурсов: В условиях ограниченности ресурсов и неопределенности внешних условий компании часто сталкиваются с необходимостью принятия решений о распределении ресурсов. Нечеткие тензорные модели могут помочь анализировать данные о потреблении ресурсов, затратах, производственных мощностях и других факторах, чтобы оптимизировать распределение ресурсов и достичь наилучших результатов.
Прогнозирование финансовых показателей: Для финансовых аналитиков и менеджеров важно иметь надежные прогнозы финансовых показателей, таких как выручка, прибыль, затраты. Нечеткие тензорные модели могут использоваться для анализа финансовых данных, учета взаимосвязей между различными факторами и прогнозирования финансовых показателей в различных сценариях.
В целом, нечеткие тензорные модели представляют собой мощный инструмент для анализа технико-экономической информации, который позволяет учитывать сложность и неопределенность реальных экономических процессов и принимать обоснованные решения в условиях неопределенности и изменчивости. [7]
- Заключение
В данной статье было рассмотрено применение нечетких тензорных моделей в анализе технико-экономической информации. Нечеткая логика и тензорные модели представляют собой мощные инструменты для работы с нечеткой и многомерной информацией, что делает их особенно полезными для анализа данных в сфере экономики и управления.
Одним из основных преимуществ нечетких тензорных моделей является их способность учитывать неопределенность и размытость данных, что позволяет более точно моделировать сложные экономические процессы и принимать обоснованные решения. Кроме того, эти модели позволяют анализировать многомерные данные, учитывая взаимосвязи между различными параметрами, что делает их эффективным инструментом для прогнозирования, оптимизации и принятия решений в условиях неопределенности и разнообразия факторов.
Примеры применения нечетких тензорных моделей включают прогнозирование спроса на продукцию, анализ эффективности производственных процессов, принятие решений о распределении ресурсов и прогнозирование финансовых показателей. В каждом из этих случаев нечеткие тензорные модели могут помочь выявить закономерности и взаимосвязи в данных, что позволит принимать более обоснованные и эффективные решения.
Таким образом, нечеткие тензорные модели представляют собой перспективное направление развития анализа данных в сфере экономики и управления, которое может значительно улучшить качество принимаемых решений и повысить эффективность бизнес-процессов.
Литература:
1. Романенко В. А. Нечеткая технико-экономическая модель системы обработки багажа аэропорта / В. А. Романенко, М. А. Скороход
2. Математические модели современных экономических процессов, методы анализа и синтеза экономических механизмов. Актуальные проблемы и перспективы менеджмента организаций в России: сб. ст. XI Всерос. науч.-практ. конф. Вып. 1. Ин-т проблем упр. им. В. А. Трапезникова Рос. акад. наук.; Самар. нац. исслед. ун-т им. С. П. Королева, под ред. Д. А. Новикова — Самара: Изд-во СамНЦ РАН, 2017. — С. 118–123.
3. Броневич, А. Г. Нечеткие модели анализа данных и принятия решений: учебное пособие / А. Г. Броневич, А. Е. Лепский.
4. Задурнова Г. В. Основы нечеткой логики. — М.: Издательский центр «Академия», 2004. — 160 с.
5. Журавлев Ю. П., Гусева Н. М. Нечеткая логика и ее применение в управлении. — М.: Инфра-М, 2017. — 288 с.
6. Чудновский В. П. Нечеткая модель экономических систем. — М.: Интеллект, 2003. — 288 с.
7. Красносельский М. А. Нечеткие множества и их применение. — М.: Высшая школа, 1990. — 240 с.
8. Розенблат Г. И. Введение в нечеткую логику. — М.: Наука, 1989. — 232 с.
9. Броневич А. Г., Лепский А. Е. Нечеткие модели анализа данных и принятия решений. — М.: Форум, 2007. — 320 с.
10. Литвинов В. Н., Сергеев В. А. Модели и методы анализа нечеткой информации. — М.: Финансы и статистика, 2003. — 272 с.







