В данной работе произведена оценка коэффициента теплоотдачи в межрёберном зазоре радиатора в режиме вынужденной конвекции. Приведены анализ и сравнение теплоотдачи в различных режимах.
Ключевые слова: теплоотдача, вынужденная конвекция, естественная конвекция, ламинарный режим.
При выборе типа охлаждения, необходимого для радиоэлектронной аппаратуры (далее РЭА), стоит учитывать большое число факторов, среди которых условия окружающей среды, максимальная температура компонентов, которых в полноценных устройствах может быть сотни тысяч. В настоящее время стремление к миниатюризации ведёт к увеличению количества теплоты, выделяемой с единицы поверхности. С этим можно бороться путём выбора материала, подходящего по теплопроводности, однако это оказывается экономически невыгодным.
Применение естественной конвекции для охлаждения компонентов РЭА является наиболее простым и дешёвым методом, но доступным только при достаточно низких температурах среды. В случае замкнутых корпусов распространённым методом охлаждения является вынужденная конвекция, которая обусловлена внешним воздействием, например, работой насоса, вентилятора или другой охлаждающей системы [1, с. 34–35].
Для подтверждения того, что теплоотдача при вынужденной конвекции более эффективна, чем при естественной, сравним коэффициенты теплоотдачи в этих двух режимах.
При получении данных о теплоотдаче радиатора были использованы электрическая схема (рис. 1) с радиатором (рис. 2), на который направлен вентилятор.
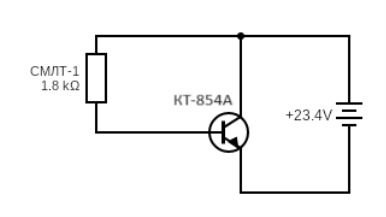
Рис. 1. Экспериментальная схема
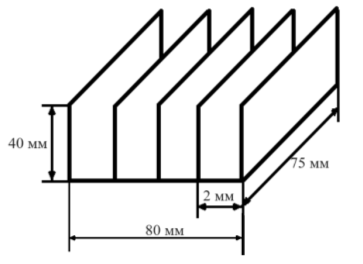
Рис. 2. Схематичное изображение радиатора
Для расчёта коэффициента теплоотдачи
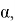
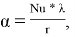
где
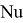
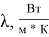
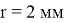
Чтобы найти число Нуссельта, необходимо определить режим течения воздуха в межрёберном зазоре. Выделяют ламинарный и турбулентный режимы. Они различаются упорядоченностью слоёв: в ламинарном потоке слои жидкости или газа перемещаются параллельно стенкам канала, не смешиваясь между собой, а при турбулентном движении возникают вихри, направление и скорости движения частиц непрерывно изменяются. Переход от ламинарного к турбулентному режиму зависят от геометрических характеристик, свойств жидкости или газа и скорости движения [1, с. 35].
Как показали исследования, с помощью числа Рейнольдса можно судить о режиме течения [1, с 44–46].
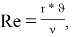
где
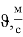
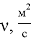
Если
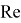
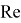
Для ламинарного режима:
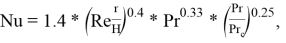
где
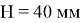
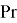
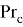
Для турбулентного режима:
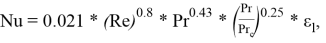
где
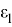
Величины
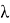
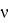
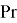
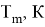
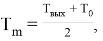
где
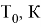
Величина
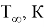
При подаче напряжения 23.4 В, на транзисторе КТ-854А выделилась мощность
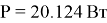
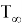
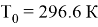
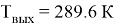
Следовательно, по формуле (5)
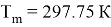
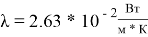
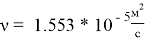
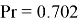
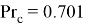
Скорость воздушного потока, измеренная с помощью термоанемометра testo 410–1,
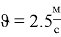
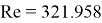
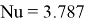
Подставив рассчитанные данные в формулу (1), был получен коэффициент теплоотдачи в режиме вынужденной конвекции
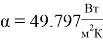
Предыдущее исследование содержит результаты эксперимента, в ходе которого был найден коэффициент теплоотдачи в режиме естественной конвекции, он равен
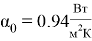
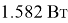
Согласно закону Ньютона-Рихмана, тепловой поток
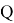
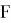
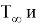
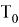
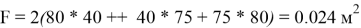
Для вынужденной конвекции:
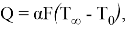
Тогда тепловой поток в процессе теплоотдачи при вынужденной конвекции
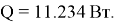
Однако отметим, что не вся мощность, выделяемая транзистором, рассеивается с помощью конвекции. Энергия передаётся также и с помощью излучения и теплопроводности. Первое играет весомую роль при естественной конвекции.
Литература:
- Пошехонов П. В., Соколовский Э. И. Тепловой расчёт электронных приборов.: учеб. пособие для вузов. М.: «Высш. школа», 1977–158 с.
- Михеев М. А., Михеева И. М. Основы теплопередачи. — 2-е изд., стереотип. — М.: «Энергия», 1977–344 с., ил.
- Исаченко В. П., Осипова В. А., Сукомел А. С. Теплопередача.: учеб. пособие для вузов — 3-е изд., перераб. и доп. М.: «Энергия», 1975–488 с., ил.
- Воронцова Т. В, Никулин Д. Р. Оценка влияния теплоотдачи излучением на тепловой баланс радиатора в режиме естественной конвекции и окружающей среды // «Лучшая исследовательская статья 2024»: Сборник статей Международного научно-исследовательского конкурса. — Петрозаводск: МЦНП «Новая наука», 2024. — с. 133–137.







