В этой статье рассматривается проблема развития культуры логического мышления учащихся на уроках математики. Анализируются особенности образовательного процесса, способствующие формированию этой культуры. Также обсуждается возможность применения такой системы обучения в рамках компетентностного подхода.
Ключевые слова : культура логического мышления, методика преподавания математики, принцип системности и систематичности.
Логическая культура является неотъемлемой частью образования современного человека, так как она способствует развитию критического мышления, аналитических навыков и умения обосновывать свои выводы. В данной статье мы рассмотрим, как происходит формирование логической культуры в процессе обучения алгебре и началам математического анализа в старших классах (10–11 классы).
Углубленное изучение алгебры и математического анализа направлено на развитие у учащихся навыков логического мышления и их способности к анализу и синтезу информации. Основными методами, используемыми для формирования логической культуры, являются:
Решение задач. Учащиеся решают задачи разного уровня сложности, что позволяет им развивать свои навыки анализа и интерпретации данных, а также применять теоретические знания на практике.
Работа с доказательствами. При изучении алгебры и анализа ученики учатся доказывать различные теоремы и утверждения, что требует от них умения логически мыслить и обосновывать свои доводы.
Применение индуктивных и дедуктивных методов рассуждения.
В математике индуктивные и дедуктивные рассуждения используются для доказательства теорем и решения задач.
Индуктивные рассуждения начинаются с наблюдений и экспериментов, а затем делаются обобщения и выводы. Например, можно провести эксперимент, задавая вопросы людям о том, как они добираются до работы, и затем сделать вывод о том, что большинство людей добираются до работы на автомобиле или общественном транспорте.
Дедуктивные рассуждения начинаются с общих утверждений (аксиом) и правил, а затем применяются к конкретным случаям. Например, можно начать с аксиомы о том, что если две прямые пересекаются, то они образуют углы, и затем применить это правило к конкретному случаю пересечения двух прямых на плоскости.
Построение математических моделей. Учащимся предлагается решать задачи с использованием математических моделей, что помогает им развить умение анализировать и синтезировать информацию.
Обучение алгоритмам и методам решения. Ученики осваивают различные алгоритмы и методы решения задач, что способствует формированию у них навыков логического мышления.
Отметим следующие компоненты логической культуры учащихся:
– умение конструировать определения математических понятий;
– умение выделять общие признаки математических понятий;
– умение выделять специфические признаки математических понятий;
– умение распознавать математические объекты по их определению;
– умение выстраивать «цепочки» умозаключений (индуктивные и дедуктивные доказательства);
– умение выявлять структуру теоремы и ее вид (простая или сложная);
– умение определять вид доказательства (прямое или косвенное);
– умение проводить рассуждения по поиску доказательства;
– умение находить логические ошибки в рассуждениях;
– умение выдвигать гипотезы и проверять их на достоверность;
– умение составлять алгоритм (план) решения задачи;
– умение классифицировать задачи по виду;
– умение классифицировать задачи по способам их решения;
– умение выбирать ключевые задачи;
– умение составлять аналогичные задачи;
– умение расчленять задачу на простые задачи;
– умение обобщать задачу;
– умение проводить исследование результатов решенной задачи;
– умение оценивать оптимальность способа решения задачи .
Приведем некоторые примеры.
У выпускника школы должно быть сформировано умение пользоваться различными методами решения задач и отыскивать оптимальное (наилучшее) решение. Поставим более узкую задачу: сформировать у учащихся умение классифицировать уравнения по способам их решения. В 11 классе у школьников уже достаточно опыта, чтобы на более высоком уровне обобщить и систематизировать знания и умения по теме «Уравнения. Способы решения уравнений». На первом этапе необходимо добиться, чтобы каждый ученик мог быстро визуально определить, к какому виду относится данное уравнение (алгебраическое, трансцендентное). Предварительно нужно составить таблицу «Классификация уравнений по виду»
|
У равнения |
|
|
Алгебраические |
Трансцендентные |
|
1. целые |
1. показательные |
|
2. дробные |
2. логарифмические |
|
3. иррациональные |
3. тригонометрические |
|
4. смешанные |
|
Пример диагностического задания на выявление уровня сформированности умения классифицировать уравнения по виду.
Задание: Определить вид уравнения (5 минут)
1 вариант
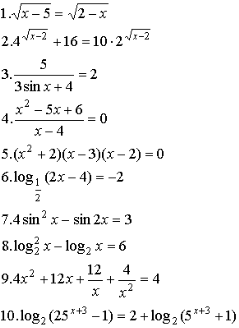
На следующем этапе формируем умения учащихся классифицировать уравнения по способам их решения. На практических занятиях при решении каждого уравнения учащиеся сначала выдвигают гипотезу о том, каким способом (возможно, и не одним) оно может быть решено. Проверяем гипотезу на достоверность, выбираем оптимальный способ решения.
После рассмотрения достаточного количества уравнений, решаемых различными способами, учащиеся смогут выделить следующие способы решения уравнений:
- Разложение левой части уравнения на множители. Применение равенства нулю произведения.
- Замена переменной.
- Возведение обеих частей уравнения в одну и ту же степень.
- Алгоритм решения однородных уравнений.
- Алгоритм решения возвратных уравнений.
- Использование свойств монотонности и ограниченности функций.
- Метод «пристального» взгляда.
Конечно, в этом списке представлены не все способы решения уравнений, но практика показывает, что именно эти способы наиболее часто применимы.
Учащиеся делятся на группы и получают задание подобрать примеры уравнений, которые решаются определённым методом, а также выявить ключевые особенности уравнений, решаемых этим методом. Затем проводится урок-семинар, где каждая группа представляет свой метод решения с интересными примерами. На основе предложенных уравнений создаётся сборник задач, который ученики могут использовать для повторения и подготовки к экзаменам.
В результате выполнения этой работы учащиеся выполняют диагностическое задание, позволяющее определить уровень их способности классифицировать уравнения по методам их решения. В зависимости от результатов диагностики проводится дополнительная работа с теми учениками, чей
уровень сформированности данного умения не соответствует требуемому.
Пример диагностического задания
Задание: указать возможные способы решения уравнения (учащиеся должны указать только номер возможного способа решения) — 10 мин.
1 вариант
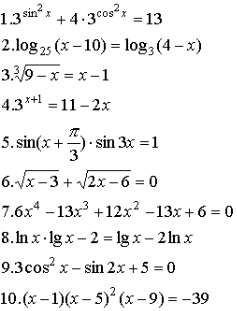
Уровни сформированности компонентов логической культуры:
- Оптимальный уровень — 86–100 %
- Допустимый уровень — 71–85 %
- Критический уровень — 50- 70 %
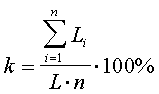
- Недопустимый уровень — менее 50 %
Коэффициент сформированности различных компонентов логической культуры вычисляется по формуле:
Где L i - количество компонентов, сформированных у i-го учащегося,
N- количество учащихся в классе,
L — количество компонентов, подлежащих исследованию
Заключение.
Таким образом, углубленное изучение алгебры и начала математического анализа способствует формированию логической культуры учащихся. Обучение включает решение задач, работу с доказательствами, применение индуктивных и дедуктивных рассуждений, построение математических моделей и освоение алгоритмов и методов решения. Все эти методы направлены на развитие критического мышления, умения анализировать и обосновывать свою точку зрения, что является важным компонентом логической культуры.
Литература:
- Рыбакина Н. А. Компетентностно-контекстная модель обучения и воспитания в общеобразовательной школе // Образование и наука. 2017. Том 19 № 2. С. 31–50.
- Никольский, С. М. Алгебра и начала математического анализа. 10 класс: А45 учеб. Для общеобразоват. Учреждений: базовый и профил. уровни / (С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин).- 8-е изд.- М.: Просвещение, 2009.- 430 с.: ил. — ISBN 978–5–09–021132–1— Текст: непосредственный.
- Виноградова, Л. В. Развитие мышления учащихся при обучении математике.-Петрозаводск, 1989.- 176 с.-глава 2. Пути развития мышления при обучении математики.- с. 66–142.







