Данная статья посвящена разработке программного обучающего тренажера в области теории принятия решений в условиях статистической неопределенности для использования в процессе аналитической работы студентов изучающих курс теории принятия решений. Существующие программные решения не предоставляют возможностей для обучения и развития практических навыков в процессе принятия решений, и являются либо комплексными инструментами профессиональной деятельности, либо предоставляют слабую интерактивность и возможности изучения задач на практике, делая упор на теоретическое изучение задачи.
В статье описана абстрактная форма типовой задачи, а также изложен ход ее решения, выделены основные трудности, с которыми сталкиваются студенты при ее изучении. С учетом этих проблем описана структура программного тренажера, каждый элемент которого специализируется в объяснении определенного этапа решения.
Теория принятия решений в условиях статистической неопределенности имеет широкое применение на практике в различных областях, базовые подходы используемые при принятии решения (теорема Байеса) используются в работе нейросетей, медицинской диагностике и прогнозировании редких заболеваний, критерии принятия решений также используются в стратегическом управлении и финансовом планировании. Широкое применение, совместно с комплексностью данного класса задач и отсутствием подходящего для их изучения ПО обуславливают актуальность и востребованность разработки обучающего тренажера.
Ключевые слова: принятие решений, статистическая неопределенность, игры с природой, обучающие программы, критерии принятия решений, визуализация принятия решений, деревья решений.
- Абстрактная структура задачи
Задачи принятия решений в условиях неопределенности также называют «играми с природой» или «статистическими играми» согласно участвующим лицам.
Первый участник игры — «природа». «Природа» — это обобщенное понятие противника, не преследующего собственных целей в конфликте, т. е. совокупность внешних обстоятельств (имеющих случайный неопределенный характер), в которых приходится принимать решения.
Второй участник игры — статистик или лицо принимающее решение (ЛПР). Цель статистика — принять решение с наибольшей для себя выгодой в условиях неопределенности о поведении «природы».
ЛПР должен сделать выбор или последовательность выборов из совокупности различных возможных действий, при этом последствия любого действия зависят от непредсказуемого события или от «состояния природы». У ЛПР имеются некоторые данные, касающиеся неопределенностей в его задаче, и какие-то суждения об этих неопределенностях. В случаях решения задач с экспериментом также имеется возможность получить дополнительную информацию по поводу этих неопределенностей за определенную стоимость [2].
- Этапы решения задачи, возникающие трудности
2.1 Формализация задачи, составление модели
При составлении моделей задач принятия решений используются следующие обозначения:
— Имеется множество стратегий ЛПР (статистика): D = {d 1 , d 2 , …, d m };
— Имеется множество состояний «природы» : S = {s 1 , s 2 , …, s n };
— Имеется функция выигрышей (или потерь ): L (d,s): k{ i , j };
— Заданы вероятности состояний «природы» (не во всех случаях): P(S) = {p 1 , p 2 , …, p n }.
При возможности проведения эксперимента(ов):
— Известны исходы экспериментов : Z = {z 1 , z 2 , …, z a } и их стоимости с(e);
— Заданы
распределение условных вероятностей
исходов при различных состояниях природы
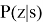
При указании исходных данных в программном тренажере используется эти обозначения, переключение между различными задачами осуществляется кнопками T [n] (рисунок 4) отдельно для каждого из двух рабочих окон программы.
2.2 Расчет апостериорных вероятностей с использованием формулы Байеса
В задачах с возможностью проведения «эксперимента» предоставляется матрица условных вероятностей исходов при тех или иных состояниях природы. Подобные распределения вероятностей обычно могут быть даны как точность каких-либо методик или статистики проведения экспериментов.
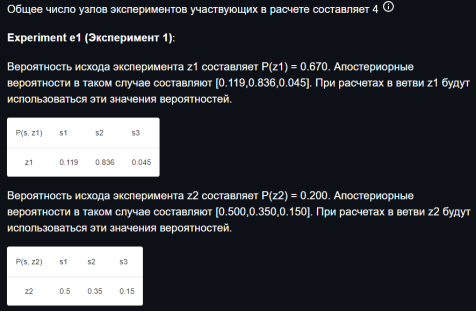
Рис. 1. Расчет апостериорных вероятностей (в программе-тренажере)
Разработанный тренажер рассчитывает необходимые для решения апостериорные вероятности с привязкой к дереву решений, рисунок 1.
2.3 Формирование дерева решений
Деревья решений в задачах теории принятия решений используются для визуализации хода принятия решений и отображения возможных исходов задачи [2]. Базовый вариант дерева решений представлен на рисунке 2.
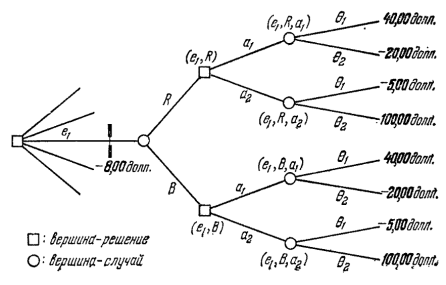
Рис. 2. Дерево решений
Описанный формат был использован в качестве основы для визуализации дерева решения, каждому типу узла присвоен свой цвет и форма, узлы эксперимента обозначаются отдельно от узлов принятия решения, дополнительно на дереве указаны соответствующие вероятности для каждой из ветвей и стоимостные оценки исходов.
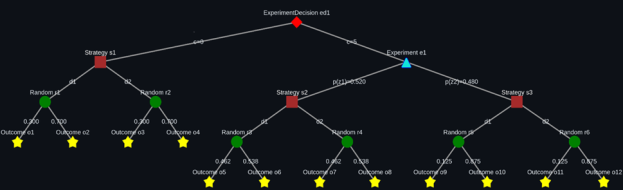
Рис. 3. Дерево решений (в программе-тренажере)
Использование интерактивного дерева решений, генерируемого на основе исходных данных задачи позволяет:
— Наглядно представить все возможные варианты решения
— Изучить влияние выбранного критерия решения на значения прогнозируемого выигрыша, как в глобальном виде, так и для любого поддерева
— Изучить влияния числа возможных состояний, стратегий, экспериментов и их исходов на вычислительную и аналитическую сложность задачи.
2.4 Расчет прогнозируемых значений с учетом выбранного критерия решения
При расчете прогнозируемых значений используются различные критерии в зависимости от предпочтений ЛПР и условия задачи, а также наличии или отсутствия априорных вероятностей. Основные критерии принятия решений, следующие:
Критерий максимальной правдоподобности — выбор стратегии, руководствуясь наиболее вероятными исходами;
Критерий Байеса — выбор стратегии, руководствуясь математическим ожиданием выигрышей;
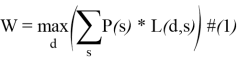
Разработанное ПО может использовать описанные выше критерии при расчетах прогнозируемых решений, формируя пошаговое описание решения и внося изменения в дерево решений на их основе.
2.5 Формирование текстового ответа в терминах задачи и терминах модели
Результатом решения задачи является сформированный план действий с указанием прогнозируемых выигрышей, учитывая возможные исходы эксперимента.
Данный план формируется в двух вариантах:
в терминах модели — с использованием условных обозначений, без описания выбранных критериев и привязки к исходному тексту задачи;
в терминах задачи — с полным описанием причин выбора стратегий, и использованием исходного текста.
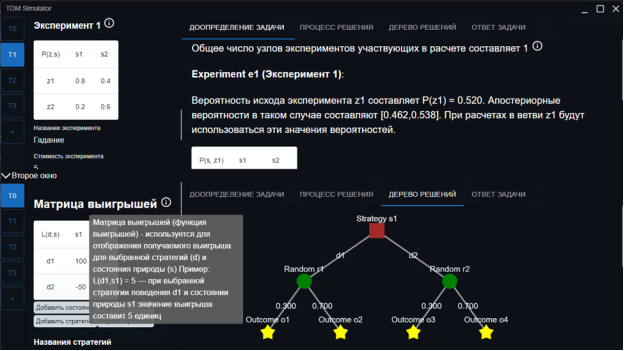
Рис. 4. Вид интерфейса разработанного тренажера
- Выводы
В настоящий момент в прототипе обучающего тренажера были реализованы все вышеописанные функции, планируется его тестирование и апробация путем проведения занятий с его использованием. На основе анализа эффективности его применения будет введен дополнительный функционал и доработан имеющийся.
Литература:
- Качурин, А. Е. Обучающий тренажёр «Принятие решений в условиях статистической неопределенности» // наука. Технологии. Инновации //Сборник научных трудов в 9 ч. / Новосибирск: Изд-во НГТУ, 2016. — Часть 1. — 137 с.
- Райфа, Г. Анализ решений. Введение в проблему выбора в условиях неопределенности / Г. Райфа. — Москва: Наука, 1977. — 408 c. — Текст: непосредственный.







