Применение моделей Васичека для прогнозирования базовых ставок в Казахстане

В современной экономической науке вопросы эффективного прогнозирования монетарных показателей занимают центральное место в стратегиях макроэкономического управления. Базовая процентная ставка, устанавливаемая центральными банками, является ключевым инструментом монетарной политики, предназначенным для контроля инфляции и стимулирования экономического роста. В Казахстане, как и в других странах с переходной экономикой, актуальность данной темы обусловлена необходимостью поддержания экономической стабильности и предотвращения финансовых кризисов.

Научное сообщество активно исследует методы прогнозирования базовой ставки, используя различные эконометрические модели. Одной из таких моделей, которая демонстрирует значительный потенциал в анализе динамики процентных ставок, является стохастическая модель Васичека. Эта модель позволяет описывать изменения ставки как случайный процесс с учётом возврата к долгосрочному среднему уровню, что особенно важно для прогнозирования в условиях экономической неопределенности.

Цель настоящего исследования — применить модель Васичека для анализа и прогнозирования базовой ставки Национального банка Казахстана. Используя исторические данные о базовых ставках, мы оцениваем параметры модели и проводим симуляцию Монте-Карло для прогнозирования будущих изменений ставок. Результаты данного исследования могут быть полезны для формирования монетарной политики и экономического планирования в Казахстане. Понимание будущих изменений в базовой ставке позволяет как государственным, так и частным секторам принимать обоснованные решения, влияющие на их финансовую стратегию и экономическую стабильность.

Базовая ставка Национального банка Казахстана служит в качестве фундаментального инструмента монетарной политики, оказывающего влияние на экономическую динамику страны. Её корректировка направлена на регулирование стоимости заемных средств в экономике, что влияет на инвестиционные решения, потребительский спрос и общий уровень цен. Путем изменения базовой ставки центральный банк старается управлять инфляцией и поддерживать финансовую стабильность, адаптируясь к текущим экономическим условиям и прогнозам развития. Это ключевой параметр, отражающий курс монетарной политики и служащий ориентиром для банковского сектора и экономики в целом.

В модели Васичека мгновенная процентная ставка описывается следующим стохастическим дифференциальным уравнением:

— -параметр, характеризующий скорость возврата к среднему значению

—

— -средний уровень процентной ставки

— - приращение Винеровского процесса

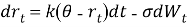
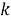
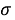
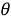
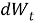
Для оценки параметров модели Васичека мы применяем метод максимального правдоподобия, используя данные из таблицы 1.

Таблица 1

Так как приращение Винеровского процесса, имеет ормальное распределение с математическим ожиданием дисперсией

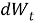
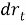
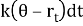
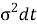
Поскольку временной интервал между наблюдениями составляет один год, мы принимаем . Следовательно, логарифм функции правдоподобия будет выглядеть следующим образом:

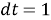
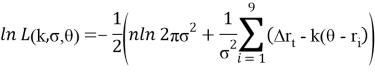
В результате мы получаем оценки параметров , ,

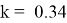
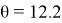
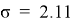
Поставляем параметры модели:

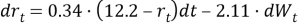
Принимая , проводим симуляцию Монте-Карло, генерируя тысячу различных сценариев на 10 лет. Сначала преобразуем уравнение в следующий вид:

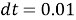
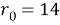
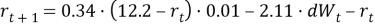
Симуляцию будем проводить на языке программирования Python 3 с использованием библиотек numpy. Код будет представлен следующим образом:

kappa = 0.3353629870679174

theta = 12.204257971669309

sigma = 2.1108289959376854

r_0 = 14

dt = 0.01

N = int(T / dt)

M = 1000

paths = np.zeros((M, N+1))

paths [:, 0] = r_0

dd= []

for i in range(1, N+1):

dw = np.random.normal(scale=np.sqrt(dt), size=M)

dd.append(dw)

paths [:, i] = paths [:, i-1] + kappa * (theta — paths [:, i-1]) * dt + sigma * dw

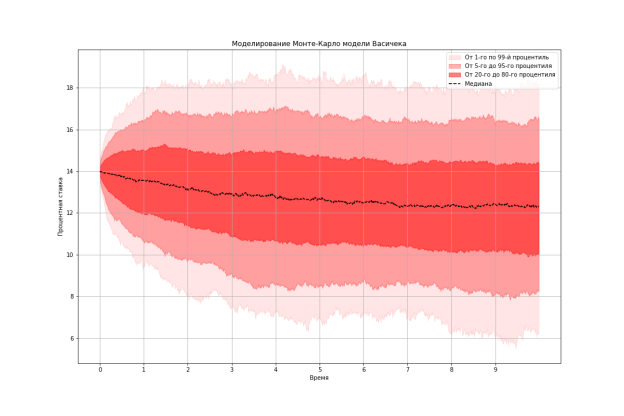
Рис. 1

Медиана прогнозов (черная пунктирная линия) представляет собой медианное значение всех симулированных траекторий на каждый момент времени. Это значение отражает наиболее вероятное направление изменения базовой ставки и является ключевым показателем для планирования монетарной политики.

Основной диапазон колебаний (темно-красная область) охватывает интервал от 20-го до 80-го процентилей распределения прогнозируемых значений, представляя собой 60 %-ный доверительный интервал. Этот диапазон указывает на основные возможные колебания ставки, которые могут быть ожидаемы в обычных экономических условиях.

Широкий диапазон колебаний (светло-красная область) охватывает интервал от 5-го до 95-го процентилей. Эта область включает в себя крайние значения, которые могут возникнуть в менее вероятных экономических сценариях, и служит показателем потенциального максимума и минимума изменений ставки.

Экстремальные колебания (самая светлая красная область) охватывают интервал от 1-го до 99-го процентилей. Эти значения представляют крайние возможные сценарии, которые могут произойти с очень малой вероятностью, и важны для анализа рисков экстремальных экономических условий.

Литература:

1. Светлов, К. В. Стохастические методы анализа рынка заимствований: специальность 08.00.13 «Математические и инструментальные методы экономики»: диссертация на соискание ученой степени кандидата экономических наук / Светлов Кирилл Владимирович; Санкт-петербургский государственный университет. — Санкт-Петербург, 2015. — 143 c. — Текст: непосредственный.
2. График принятия решений по базовой ставке 2015–2024. — Текст: электронный // Нацбанк: [сайт]. — URL: https://www.nationalbank.kz/ru/news/grafik-prinyatiya-resheniy-po-bazovoy-stavke/rubrics/2098 (дата обращения: 10.05.2024).