На основе метода теплового потока предложены численные модели расчета эффективной теплопроводности композиционных систем. Представлены стационарная и неравновесная модели. Выполнены расчеты эффективной теплопроводности полимерных композитов с различными наполнителями. Показано, что учет только теплопроводностей матрицы и наполнителя не обеспечивает хорошего согласования с экспериментальными данными.
Метод теплового потока заключается в расчете температурного поля композита и далее вычислении теплового потока, через который определяется эффективная теплопроводность композита.
Дифференциальное уравнение теплопроводности имеет вид:
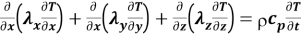
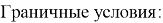
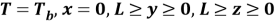
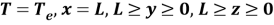
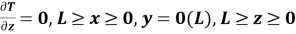
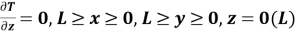
Решение задачи представим в конечно-разностном виде в соответствии со схемой, представленной на рисунке 1 (стационарная задача).
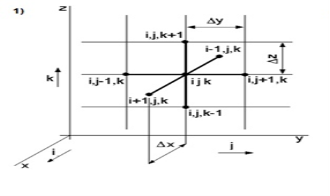
Рис. 1. Схема «Крест» численного решения уравнения (1)
Уравнение (в конечных разностях для нестационарного случая) имеет вид:
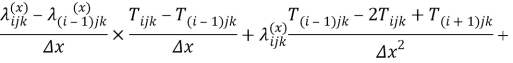
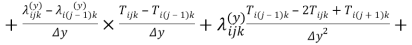
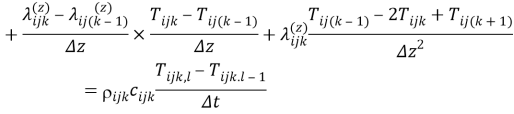
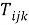
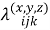
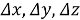
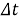
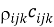
Преобразование уравнения (2) для нестационарного случая для температурного поля дает модель
Температура узла может быть представлена через температуры соседних узлов:
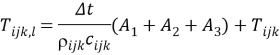
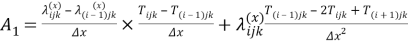
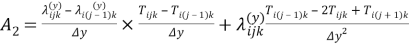
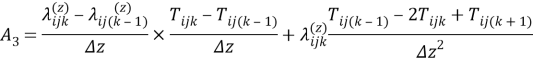
Для устойчивости численного решения должно выполняться условие:
Fo
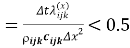
В стационарном случае температурное поле определяется соотношениями:
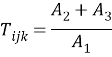
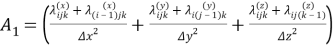
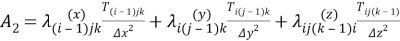
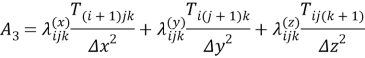
После расчета температуры в узлах решетки рассчитывается среднеее значение потока в каждом узле и далее эффективный коэффициент теплопроводности.
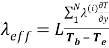
Представим ещё одну модель теплопроводности композита. Это наиболее ранняя модель и принадлежит Максвеллу.
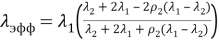
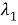
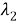
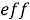
На рисунке 2 представлены экспериментальные и расчетные данные эффективной теплопроводности композита на основе эпоксидной смолы с наполнителем из двуокиси кремния (SiO 2 ). Расчеты выполнены в соответствии с моделями (3), (4), (6).
Задача (3) решена явным методом. Задаются пространственные и временной шаги дискретной сетки.
На гранях y=0 и y=L (L — линейный размер образца) задаются граничные условия 1 рода. На всех других гранях имеют место адиабатические граничные условия. Начальные значения во внутренних узлах могут быть произвольными. Однако для оптимизации численных вычислений принимается начальное линейное распределение. По температуре на предыдущем шаге вычисляются все текущие температуры в узлах до тех пор, пока значения температуры во внутренних узлах перестанут изменяться (с конечной точностью).
Задача (4) решена методом релаксации. Граничные условия принимаются аналогичными как в предыдущей модели. Далее по формулам (4) осуществляется релаксационный процесс до тех пор, пока значения температуры во внутренних узлах перестанут изменяться (с конечной точностью).
Численные модели (3) и (4) дают разбежку не более 0,5 %
![Расчетные и экспериментальные [2] данные эффективной теплопроводности композита на основе эпоксидной смолы с наполнителем из двуокисикремния (SiO2)](https://moluch.ru/blmcbn/114003/114003.030.png)
Рис. 2. Расчетные и экспериментальные [2] данные эффективной теплопроводности композита на основе эпоксидной смолы с наполнителем из двуокисикремния (SiO 2 )
Необходимость выполнения рассмотренных расчетов связана с созданием материалов с прогнозируемыми физическими свойствами. На эффективную теплопроводность композита влияет очень много факторов — от рассмотренных в моделях теплопроводностей матрицы и наполнителя, их процентного соотношения — до процессов кластеризации частиц наполнителя, учета межфазного и контактного тепловых сопротивлений, способа активизации частиц наполнителя, размеров и формы частиц. Все эти факторы могут быть учтены в численных расчетах, что обеспечит требуемое согласование теории и экспериментальных данных.
Литература:
- Nikitin, A. V. Experiment and simulation of the effective thermal conductivity of composite systems based on polymers / A. V. Nikitin [et all] // Вестн. Гродно. гос. ун-та. Сер. 2, Математика. Физика. Информатика, Вычислительная техника и управление, 2019. — Т.9. –№ 3. –С. 94–103.
- R Kochetov1, Modelling of the thermal conductivity in polymer nanocomposites and the impact of the interface between filler and matrix // A V Korobko, T Andritsch1, P H F Morshuis, S J Pickenf and J J Smit1.// J. Phys. D: Appl. Phys. 44 (2011) 395401 (12pp)







