В статье автор проводит экспериментальное исследование нейросетевых методов построения однокадрового сверхразрешения.
Ключевые слова: диффузионная вероятностная модель, генеративно-состязательная сеть, получение сверхразрешения, глубокое обучение.
1 Нейросетевые методы построения сверхразрешения
В последнее время для построения сверхразрешения набрал популярность подход, использующий генеративные модели. Такие модели нейронный сетей позволяют создавать новые изображения, которые похожи на исходный набор изображений.
1.1 Генеративно-состязательная сеть
Данную модель нейронной сети впервые описал Ян Гудфеллоу в 2014 году [1]. Основной подход обучения построен на комбинации двух нейронных сетей, первая из которых является генератором, а вторая — дискриминатором. Как уже было сказано генеративная сеть создаёт некие объекты. Роль дискриминативной заключается в попытке отличить сгенерированные объекты от подлинных. При этом архитектура обоих сетей может быть произвольной. Однако при работе с изображениями дискриминатором выбирают сверточную сетью, которая выполняет роль классификатора, а генератор «разворачивает» изображение из набора случайных чисел, которые он получает на вход.
1.2 Диффузионная вероятностная модель
Данная модель была представлена в 2015 году, но получила распространение после 2020 года [2, 3]. Суть модели заключается в использовании цепей Маркова для преобразования известного простого распределения, например гауссовского, в нужное, то есть распределение изображения. Так как каждое следующее состояние в цепях Маркова зависит только от предыдущего и процесс идёт в обе стороны, то за конечное число шагов можно получить из распределения наших обучающих данных другое распределение.
2 Проведение экспериментальных исследований
Цель эксперимента заключается в сравнении моделей нейронных сетей и нахождение лучшей модели по заданным метрикам на различных классах данных.
В эксперименте использовались метрики PNSR и SSIM. PNSR определяется как:
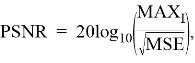
где
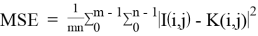
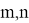
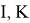
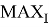
SSIM рассчитывается так:
SSIM
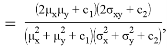
где
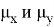
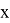
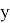
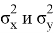
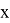
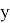
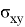
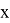
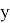
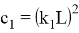
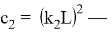
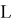
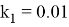
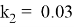
При исследовании использовались наборы данных: CelebA и BSD.
2.1 Постановка эксперимента
Для сравнения используются описанные раньше модели. Для каждой из них будут найдены параметры, при которых модели будут выдавать наилучшие показатели метрик для сгенерированных изображений на различных наборах данных. После нахождения лучших параметров для каждой сети и каждого набора данных будет проведено сравнение результатов.
2.2 Проведение эксперимента
Вначале были проведены эксперименты для каждой реализации на наборе данных CelebA. Полученные результаты приведены в таблицах 1, 2 и 3.
Таблица 1
Результаты генеративно-состязательной сети
|
Batch size |
Learning rate |
PSNR |
SSIM |
|
12 |
0.001 |
24.940 |
0.643 |
|
12 |
0.0001 |
24.989 |
0.651 |
|
12 |
0.00001 |
24.953 |
0.648 |
|
16 |
0.001 |
25.013 |
0.652 |
|
16 |
0.0001 |
2 5 .098 |
0.6 7 0 |
|
16 |
0.00001 |
25.024 |
0.659 |
|
20 |
0.001 |
24.972 |
0.646 |
|
20 |
0.0001 |
25.025 |
0.661 |
|
20 |
0.00001 |
24.996 |
0.650 |
Таблица 2
Результаты диффузионной модели при зафиксированном количестве размера канала
|
Количество шагов диффузии |
PSNR |
SSIM |
|
100 |
24.414 |
0.6723 |
|
200 |
24.924 |
0.7012 |
|
500 |
25.332 |
0.7294 |
|
900 |
25.443 |
0.7414 |
|
1000 |
25.756 |
0.7579 |
|
1250 |
25.448 |
0.7503 |
|
1500 |
25.443 |
0.7448 |
Таблица 3
Результаты диффузионной модели при зафиксированном количестве шагов диффузии
|
Размер канала |
PSNR |
SSIM |
|
8 |
22.151 |
0.7008 |
|
16 |
24.342 |
0.7179 |
|
32 |
24.894 |
0.7264 |
|
64 |
25.756 |
0.7579 |
|
128 |
25.409 |
0.7485 |
Проведём эксперименты для каждой реализации на наборе данных BSD. Полученные результаты приведены в таблицах 4, 5 и 6.
Таблица 4
Результаты генеративно-состязательной сети
|
Batch size |
Learning rate |
PSNR |
SSIM |
|
8 |
0.001 |
19.340 |
0.508 |
|
8 |
0.0001 |
19.051 |
0.443 |
|
8 |
0.00001 |
18.879 |
0.431 |
|
12 |
0.001 |
20.98 4 |
0.539 |
|
12 |
0.0001 |
19.892 |
0.523 |
|
12 |
0.00001 |
18.941 |
0.449 |
|
16 |
0.001 |
19.251 |
0.503 |
|
16 |
0.0001 |
19.149 |
0.491 |
|
16 |
0.00001 |
18.931 |
0.444 |
Таблица 5
Результаты диффузионной вероятностной модели при зафиксированном количестве размера канала
|
Количество шагов диффузии |
PSNR |
SSIM |
|
100 |
15.318 |
0.3312 |
|
200 |
15.756 |
0.3635 |
|
500 |
16.450 |
0.4015 |
|
900 |
16.960 |
0.4109 |
|
1000 |
16 . 817 |
0 . 4097 |
|
1250 |
16.840 |
0.4091 |
|
1500 |
16.821 |
0.3998 |
В результате экспериментального исследования видно, что при тестировании на наборе данных CelebA лучший результат показала диффузионная вероятностная модель, но при проверке на наборе данных BSD заметно лучший результат получился на генеративно-состязательной сети. Это можно объяснить тем, что в диффузионная вероятностная модель учится переходить из одного известного пространства данных в другое неизвестное, а также для обучения требуется только одна сеть. Что помогает сети получать лучшие результаты на тех же классах изображений. При этом на других классах изображений получается гораздо худший результат. С другой же стороны для обучения генеративно-состязательной сети требуется не только обучить сети генератора и дискриминатора, но и обеспечить «равномерность» и одновременность их обучения. При этом такое равномерное обучение позволяет добиться того, что обе сети не будут переобучаться.
Литература:
1 Generative Adversarial Nets / I. J. Goodfellow, Jean Pouget-Abadie, Mehdi Mirza [и др.]. — Текст: непосредственный // Advances in Neural Information Processing Systems 27. — 2014. — С. 2672–2680.
2 Deep Unsupervised Learning using Nonequilibrium Thermodynamics. — Текст: электронный // arxiv.org: [сайт]. — URL: https://arxiv.org/abs/1503.03585 (дата обращения: 16.05.2024).
3 Denoising Diffusion Probabilistic Models. — Текст: электронный // arxiv.org: [сайт]. — URL: https://arxiv.org/abs/2006.11239 (дата обращения: 16.05.2024).







