В настоящее время считается, что лучший профиль, обладающий максимальным моментом сопротивления, является двутавр. В тоже время известно, что двутавровые профили обладают малыми моментами инерции на кручение, т. к. эти профили не замкнуты (табл. 1).
Деформируя любой трубчатый профиль в эллиптическое сечение, мы можем значительно повысить прочность трубы на изгиб.
Эллиптический трубчатый профиль может быть получен непосредственно при прокате трубы, установкой клети для дополнительного обжатия готовой трубы и получения эллиптического профиля.
Покажем, при каком соотношении внешних габаритов нового профиля момент сопротивления Wxдостигнет максимума.
Введём следующие обозначения:
А — площадь поперечного сечения трубы;
t –толщина стенки трубы;
а, b — расстояния от центра тяжести эллиптического профиля до середины толщины стенки;
![]() – внешний габарит эллиптического профиля по оси Х.
– внешний габарит эллиптического профиля по оси Х.
Введем коэффициент ![]()
![]() тогда
тогда ![]() .
.
В соответствии с введенным коэффициентом минимальный габарит эллиптического профиля:
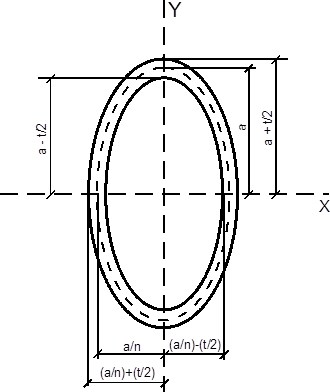
Рис. 1. Эллиптический трубчатый профиль
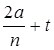 — внешний габарит эллиптического профиля по оси Y.
— внешний габарит эллиптического профиля по оси Y.
Аналогичным образом записываем размеры полости:
![]() — максимальный габарит полости;
— максимальный габарит полости;
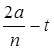 — минимальный габарит полости.
— минимальный габарит полости.
Считаем, что площадь поперечного сечения A и толщина стенки t величины постоянные (см. рис. 1).
Площадь поперечного сечения эллипса [1, с. 76]:
![]() (1)
(1)
тогда ![]() (2)
(2)
Момент инерции относительно оси Х:
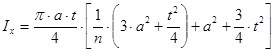 (3)
(3)
Момент сопротивления по средней линии относительно оси Х:
![]() (4)
(4)
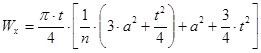 (5)
(5)
![]() (6)
(6)
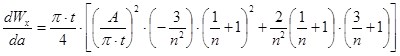 (7)
(7)
Получим уравнение третьей степени, показывающее, при каком n момент сопротивления Wx достигает максимальной величины.
![]()
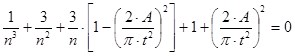 (8)
(8)
Например, для трубы диаметром 1020 мм
А=100 pсм2t=1см
![]()
![]()
![]()
Для тонкостенных профилей получаем максимум момента сопротивления ![]() при
при ![]()
Подставив n=3, получим формулы ![]() ,
, ![]() .
.
Момент инерции относительно оси Х:
![]() (9)
(9)
Момент сопротивления относительно оси Х:
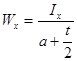 (10)
(10)
Момент инерции относительно оси Y:
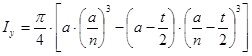 (11)
(11)
Момент сопротивления относительно оси Y:
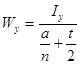 (12)
(12)
Статический момент полусечения:
![]() (13)
(13)
Момент инерции при кручении и радиусы инерции эллиптического трубчатого профиля записываем в соответствии со справочником по сопротивлению материалов [1, с. 77].
Сравнение двутавровых профилей с эллиптическими приведем в табличной форме.
Увеличение моментов сопротивления ![]() ,
, ![]() , моментов инерции
, моментов инерции ![]() ,
, ![]() , радиусов инерции
, радиусов инерции ![]() ,
, ![]() эллиптических профилей по отношению к двутавровым профилям (характеристики двутавровых профилей приняты за единицу).
эллиптических профилей по отношению к двутавровым профилям (характеристики двутавровых профилей приняты за единицу).
Таблица 1
Сравнение двутавровых профилей с эллиптическими
|
Профили |
|
|
|
|
|
|
|
30Б1 Þ 0 |
1,265 |
2,63 |
2,96 |
4,38 |
1,72 |
2,06 |
|
50Б1 Þ 0 |
1,159 |
2,96 |
2,388 |
5,04 |
1,55 |
2,21 |
|
100Б1 Þ 0 |
1,067 |
3,62 |
1,9 |
6,7 |
1,38 |
2,57 |
|
30Ш1 Þ 0 |
1,454 |
1,91 |
4,09 |
2,63 |
2,03 |
1,63 |
|
50Ш1 Þ 0 |
1,366 |
2,07 |
3,59 |
2,95 |
1,89 |
1,72 |
|
70Ш1 Þ 0 |
1,228 |
2,58 |
2,76 |
4,165 |
1,66 |
2,04 |
|
23К1 Þ 0 |
1,943 |
1,52 |
7,79 |
1,94 |
2,78 |
1,4 |
|
40К1 Þ 0 |
1,882 |
1,55 |
7,33 |
1,55 |
2,7 |
1,41 |
|
40К2 Þ 0 |
1,903 |
1,55 |
7,4 |
1,55 |
2,72 |
1,42 |
Из таблицы сравнения видно, что максимальный эффект по увеличению момента сопротивления ![]() при замене колонного профиля 23К1. Увеличение
при замене колонного профиля 23К1. Увеличение ![]() произошло в 1,943 раза. По моменту сопротивления
произошло в 1,943 раза. По моменту сопротивления ![]() наибольший эффект возник у двутавра 100Б1. Увеличение
наибольший эффект возник у двутавра 100Б1. Увеличение ![]() в 3,62 раза. Наибольший эффект по моментам инерции возник при замене этих же профилей.
в 3,62 раза. Наибольший эффект по моментам инерции возник при замене этих же профилей. ![]() увеличился в 7,79 раза (23К1) и
увеличился в 7,79 раза (23К1) и ![]() увеличился в 6,7 раза (100Б1). Увеличение радиусов инерции
увеличился в 6,7 раза (100Б1). Увеличение радиусов инерции ![]() и
и ![]() возникло при замене этих же профилей. Увеличение
возникло при замене этих же профилей. Увеличение ![]() в 2,78 раза (23К1) и
в 2,78 раза (23К1) и ![]() в 2,75 раза (100Б1). Как и следовало ожидать, замена колонных профилей приводит к большему эффекту.
в 2,75 раза (100Б1). Как и следовало ожидать, замена колонных профилей приводит к большему эффекту.
Из этого следует, что новые эллиптические трубчатые профили найдут широкое применение в подкрановых конструкциях, для перекрытия значительных пролетов (18 … 24 метра), при замене решетчатых конструкций промышленных и гражданских зданий.
Особенность новых профилей — отсутствие концентраторов напряжений и амортизирующая способность профиля за счет своей формы сечения.
Литература:
1. Писаренко Г. С. Справочник по сопротивлению материалов / Г. С. Писаренко, А. П. Яковлев, В. В. Матвеев // 2-е изд., перераб. и доп. — Киев, 1988. — 736 с.







