О разрешимости обратной задачи определения функции источника для двумерного псевдопараболического уравнения



Работа посвящена исследованию одной линейной обратной задачи определения источника для двумерного псевдопараболического уравнения. Обратная задача заключается в нахождении функции источника, не зависящей от одной пространственных переменных из начально-краевой задачи в двумерном псевдопараболическом уравнении по переопределению во внутренней точке. Доказывается однозначная разрешимость рассматриваемой задачи.

Ключевые слова: псевдопараболическое уравнение, обратная задача, неизвестный источник, переопределение во внутренней точке.

The work is devoted to the study of one linear inverse problem of determining the source for a two-dimensional pseudoparabolic equation. The inverse problem consists of finding a source function independent of one spatial variable from the initial boundary value problem in a two-dimensional pseudoparabolic equation by redefinition at an interior point. The unique solvability of the problem under consideration is proved.

Key words: pseudoparabolic equation, inverse problem, unknown source, redefinition at an interior point.

В этой работе рассматривается задача идентификации функции источника, которое не зависят от одной из пространственных переменных. Дополнительное условие задается на плоскости, ортогональной той переменной, от которой искомый коэффициент не зависит.

В работе [1] изучены различные прямые и обратные задачи для псевдопараболического уравнения. А в работах [2–4] для двумерного псевдопараболического исследованы вопросы о построении фундаментального решения и с ее помощью изучены различные прямые задачи. В работах [5–6] исследованы одномерные и двумерные обратные задачи для псевдопараболического уравнения.

Введем обозначение:

– пространство функций , определенных в Q _T и таких, что

при ;

– класс функций , заданных на Q _T , для которых имеет место оценка;

, — вещественное число, ;

– класс функций , для которых имеет место оценка , ;

— множество функций из которые вместе со своими производными вплоть до порядка ( n,m ) принадлежат , т. е. при , аналогично определяется пространство

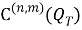
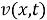
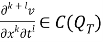
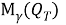
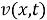
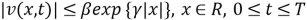
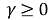
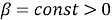
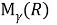
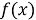
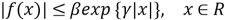
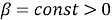
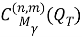
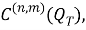
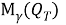
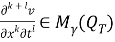
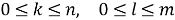
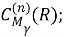
Пусть

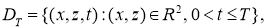
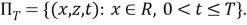
Постановка задачи . Рассмотрим в области задачу Коши

(1)

(2)

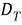
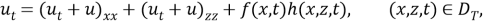
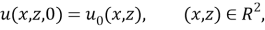
где -действительные заданные функции.

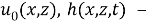
Обратная задача. Требуется найти пару функций

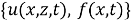
из соотношений (1) -(2), если она удовлетворяют следующим условиям переопределения

(3)

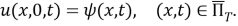
Теорема 1. Пусть функции абсолютно интегрируемы со всеми производными вплоть до второго порядка на , и для функций , выполнены условия согласования

, кроме того, на . Тогда существует единственное решение обратной задачи (1) — (3).

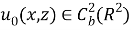
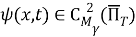
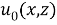
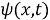
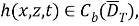
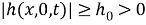
Доказательство. Для доказательства теоремы сначала приведем задачу (1) -(3) к некоторой вспомогательной задаче.

Положив в (1), и учитывая (3), получим

.

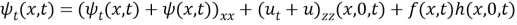
нли

(4)

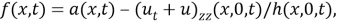
где

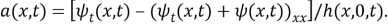
Подставляя (4) в (1), имеем

(5)

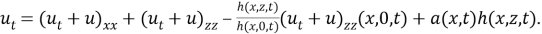
Пусть

(6)

(7)

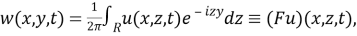
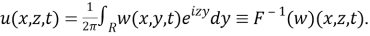
Применяя к уравнению (5) преобразование Фурье по переменной z, и учитывая то, что

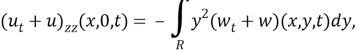
получим

(8)

(9)

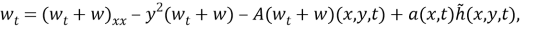
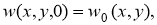
где

.

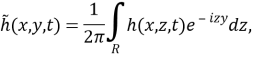
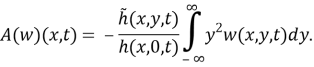
Далее будем исследовать задачу (8), (9).

Используя фундаментальное решение оператора

построенное в [1], задачу (8)-(9) заменим интегральным соотношением (10)

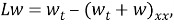
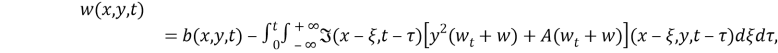
где

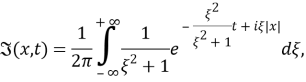
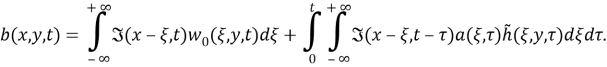
Введем новую неизвестную функцию . Тогда уравнение (8) можно переписать в виде

(11)

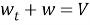
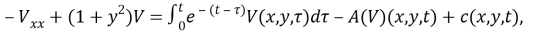
где

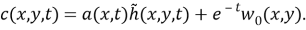
Обращая в уравнении (11) оператор , получим

(12)

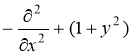
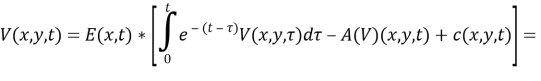
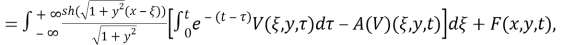
где

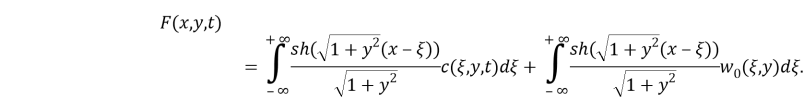
Систему уравнений (9), (10) перепишем в виде

(13)

(14)

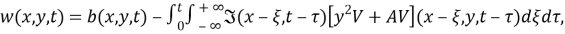
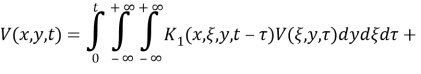
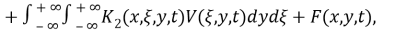
где

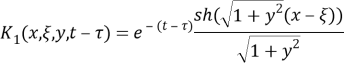
Система (13), (14) представляет собой систему линейных интегральных уравнений второго рода. Из наложенных ограничений на

следует, что функция является ограниченной и непрерывной на . В условиях теоремы эта система имеет единственное решение. Сначала из (14) находим функцию , затем из (11), (7) находим и .

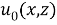
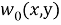
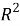
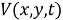
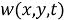
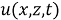
Теорема 1 доказана.

Замечание 1. Для задачи (1) — (3) можно доказать теорему устойчивости в целом.

Литература:

1. Аблабеков Б. С. Обратные задачи для псевдопараболических уравнений. — Бишкек: Илим, 2001. — 183 с.
2. Аблабеков Б. С. Решение двумерной задачи фильтрации жидкости // Вестн. Кыргызск. гос. нац. ун-та. Сер. естественно-техн. науки. — Бишкек. 1999. –Вып.1, Ч.1.-С. 61–65.
3. Аблабеков Б. С. Фундаментальное решение задачи Коши для двумерного уравнения фильтрации жидкости в трещиновато- пористой среде//Известия КГТУ им.И.Раззакова, № 9, Бишкек 2009. — С.8–101.
4. Аблабеков Б. С., Байсеркеева А. Б. Явное решение задачи Коши для двумерного псевдопараболического уравнения //Известия вузов Кыргызстана. 2015. № 10. С. 3–7.
5. Аблабеков Б. С. Двумерная обратная задача для псевдопараболического уравнения третьего порядка //Вестник КазНПУ им.Абая,сер.физ.-математ.науки, № 2(13)2005. — С.13–19.
6. Аблабеков Б. С., Байсеркеева А. Б. Обратная задача определения источника в двумерном псевдопараболическом уравнении. Случай задачи Коши // Современные проблемы физико-математических наук. Материалы III Международной научно-практической конференции 23–26 ноября 2017 г., Орел.- C.11–14.