В статье показано применения некоторых простых геометрических способов, в частности применения метода n-прямых к решению поставленных задач [1, 2, 3, 4, 5, 6, 7, 8]. В данной работе получены интересные результаты исследования, которые ранее не были опубликованы.
1) Как известно [3; 4; 5] если
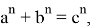
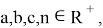
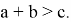
Здесь не нарушая общности можно предположить, что
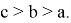
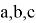
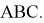
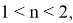
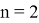
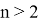
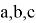
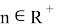
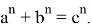
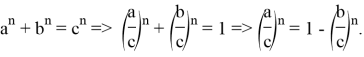
Если при этом построить график функций
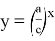
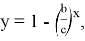
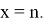
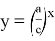
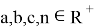
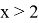
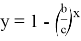
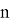
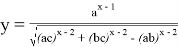
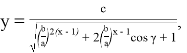
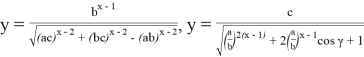
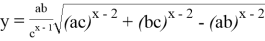
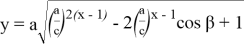
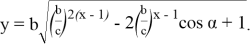
Здесь
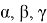
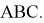
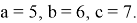
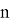
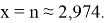
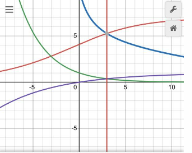
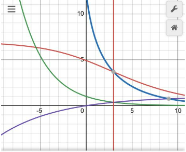
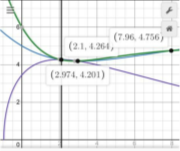
Рис. 1Рис. 2Рис. 3
Отсюда как вывод получается, что, если
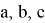
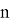
Действительно, так как для любого числа
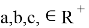
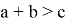
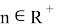
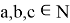
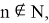
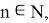
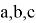
2) А теперь рассмотрим графики кривых вида
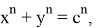
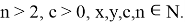
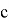
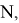
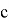
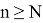
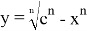
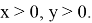
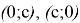
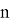
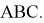
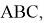
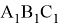
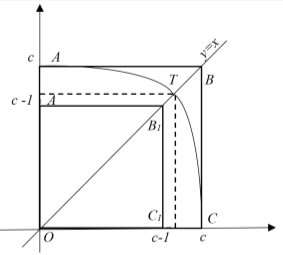
Рис. 4
Тогда пересечения
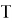
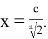
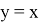
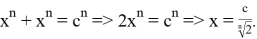
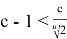
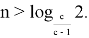
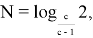
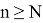
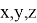
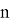
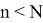
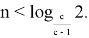
Докажем следующее неравенство
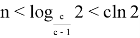
Проведем следующие преобразования:
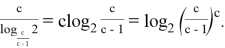
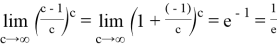
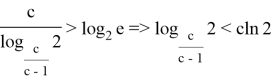
3) Мы показали [3; 6], что если провести n-прямую, то она делит противоположную сторону в отношении
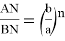
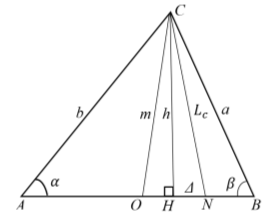
Рис. 5
В остроугольном треугольнике высоте
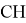

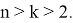

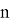
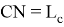

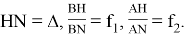
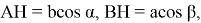
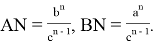
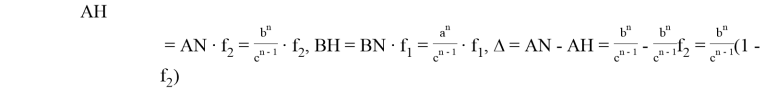
или
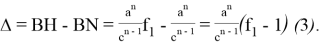
Эти формулы можно также написать в виде:
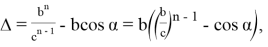
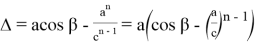
С другой стороны,
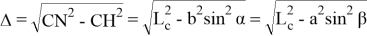
Также после некоторых преобразований можно получить формулы:
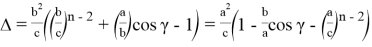
4) А теперь получим некоторые формулы для

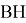
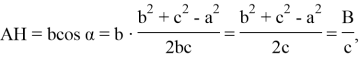
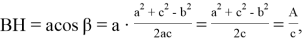
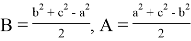
Можно показать, что при
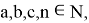
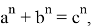
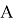
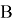
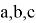
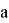
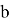
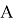
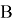
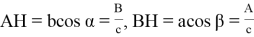
Покажем, что
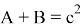
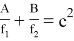
Действительно
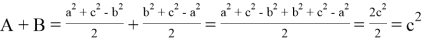
С другой стороны учитывая что
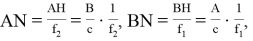
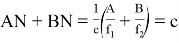
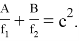
Если в формуле (10) введем обозначения
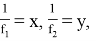
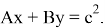
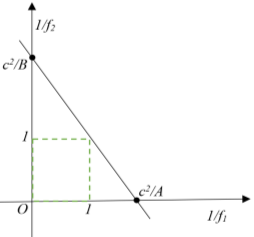
Рис. 6
Напишем последнее в виде уравнения в отрезках:
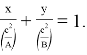
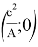
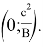
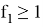
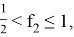
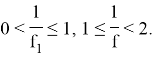
5) Так как для любого остроугольного треугольника со сторонами
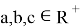
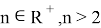
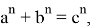
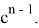
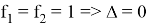
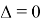
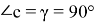
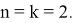
Также из рис. 7 видим, что
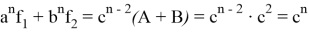
То есть одновременно с равенством
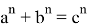
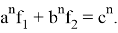
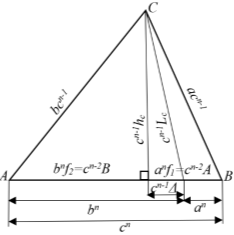
Рис. 7
6) А теперь выясним если бы
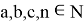
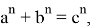
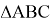
Как видно из рис. 7 все числа
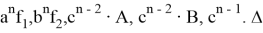
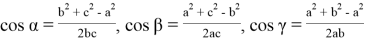
можно утверждать, что

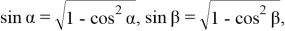
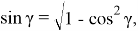
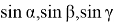
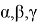
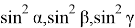
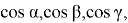
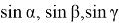
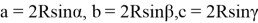
учесть в формулах (12), получим следующие формулы:
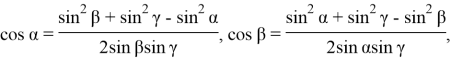
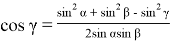
Как видно, если
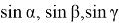
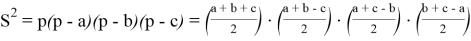
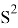
Следует отметить, что из формулы, полученной нами,
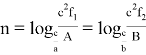
7) А теперь получим некоторые формулы, связанные с площадью
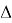
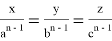
Проведем некоторые преобразования:
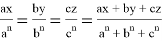
Так как точка пересечения прямых n находится на средней линии параллельно стороне c , то можно написать следующие формулы:
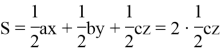
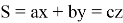
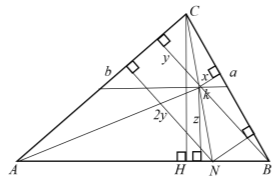
Рис. 8
А теперь используя формулы (15) и (17) можно написать следующие соотношения:
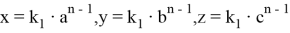
Подставляя (18) в (17), получаем:
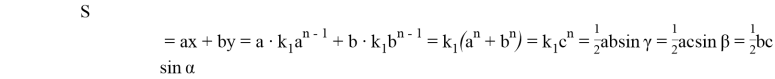
или
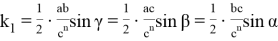
Подставляя значения (20) в (18), получаем:
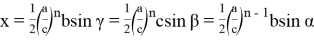
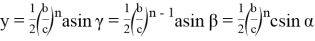
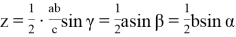
С другой стороны, используя формулы (16), (17) получаем:
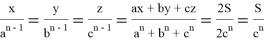
или
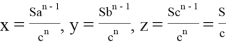
Ниже без доказательства дадим некоторые формулы:
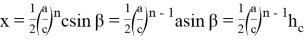
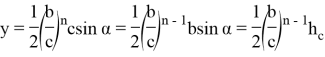
Если
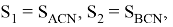
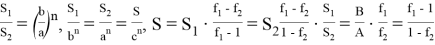
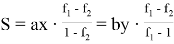
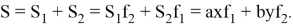
Также напишем следующие формулы (рис. 9)
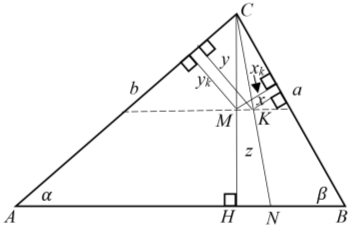
Рис.9
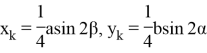
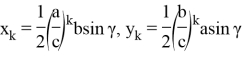
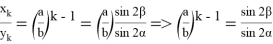
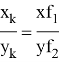
8) На рис. 11 из вершины с проведены 7 линии до пересечения основания АВ .
Как была отмечено,
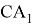
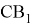
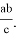
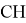
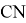
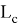
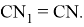
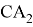
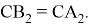
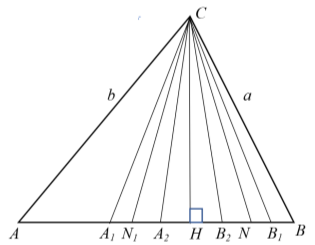
Рис. 10
Напишем расстояния между этими семью точками. Некоторые расстояния мы уже находили. Без доказательства напишем все эти расстояния:
Пусть
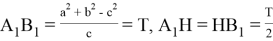
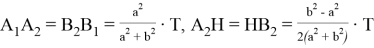
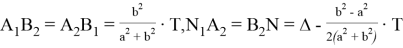
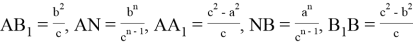
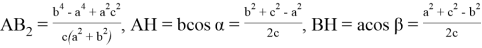
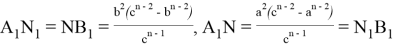
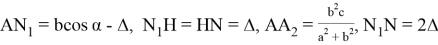
Отметим следующие отношения:
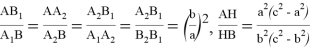
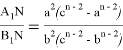
Следует отметить, что при получении некоторых формул также использовано полученное следующее новое свойство пропорции:
Если
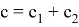
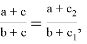
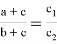
9) В связи громоздкостью покажем без выводов некоторые формулы, которые ранее не были опубликованы:
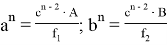
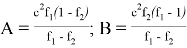
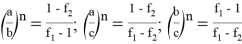
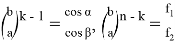
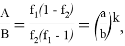
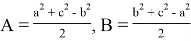
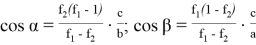
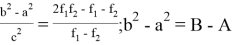
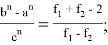
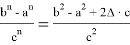
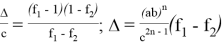
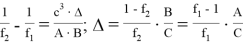
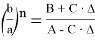
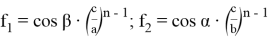
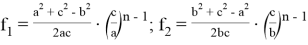
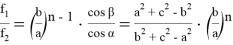
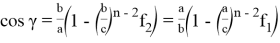
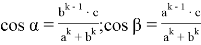
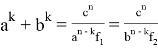
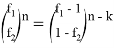
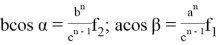
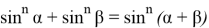
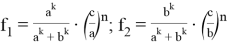
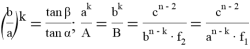
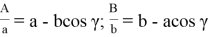
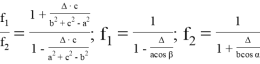
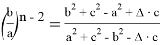
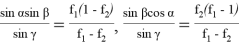
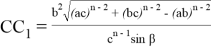
Здесь n степень прямой CN (рис.9)
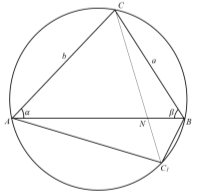
Рис. 11
10) А теперь покажем некоторые неравенства без доказательства при условии
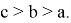
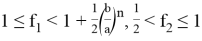
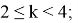
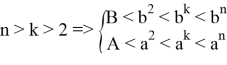
при
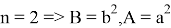
при
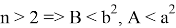
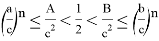
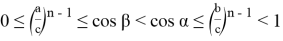
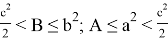
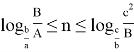
при
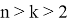
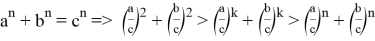
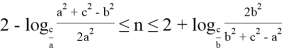
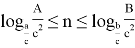
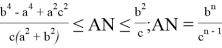
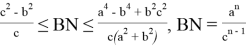
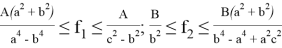
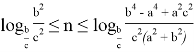
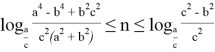
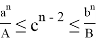
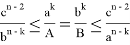
Если
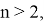
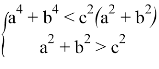
Если
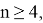
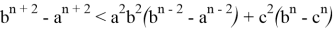
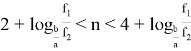
11). В
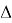
Пусть точка К является точкой пересечения
n-
прямых. Проведем параллели
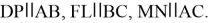
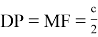
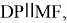
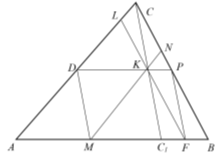
Рис. 12
Для
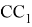
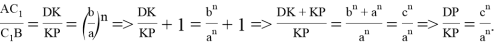
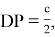
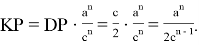
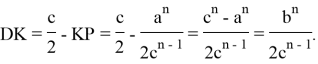
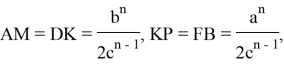
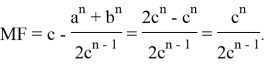
Тогда
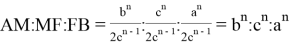
Следовательно, как видно параллели пересекают стороны треугольника, так что отношение отрезков, расположенной на одной стороне треугольника, равно отношению n -х степеней соответствующих сторон треугольника [1,2]. Определим длины всех шесть отрезков на которые делят параллели стороны треугольника.
Из подобия треугольников
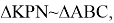
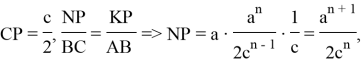
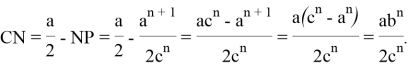
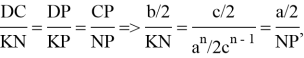
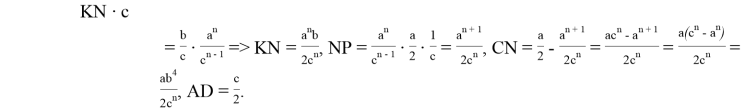
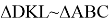
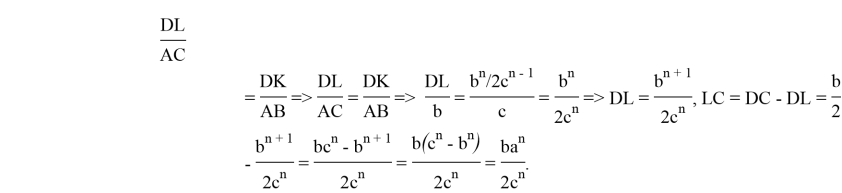
Учитывая полученные выражения, можно получить следующие отношения:
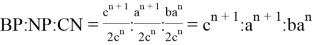
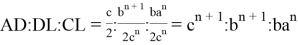
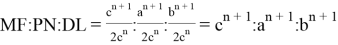
12) Пусть к является точкой пересечения
n-
прямых. Предположим эти прямые делят углы при вершине соответственно на углы
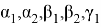
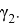
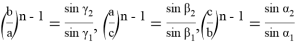
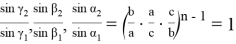
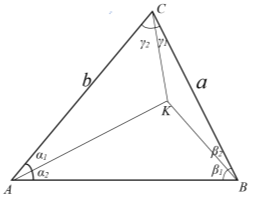
Рис. 13
Последнее является формулой Чевы для синусов.
13) Как известно [3],
n
прямые проведенные с вершин
C
треугольника

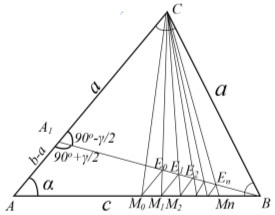
Рис. 14
А теперь определим следующие отношения:
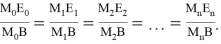
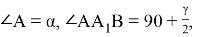
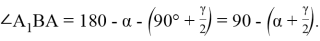
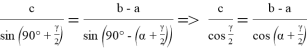
Так как искомые отношения равны
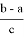
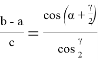
Нетрудно показать, что последняя формула является формулой Молвейде. Действительно,
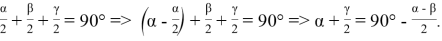
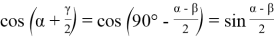
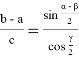
Таким образом для искомых отношений получаем:
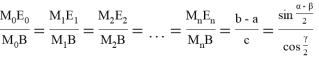
Таким образом в данной статье получены интересные формулы, связанные с применением метода n- прямых. Эту работу можно рассматривать как продолжение работ [3; 6].
Литература:
- Зетель С. И. Сборник статей по элементарной и началам высшей математики. Математическое просвещение, серия 1.1,1934, с. 5–8.
- Зетель С. И. Новая геометрия треугольника. Пособие для учителей. Москва, 1962, с. 120–129.
- Бегляров Э. Б., Гасанов И. Р. Применение метода n-прямых к решению задач. Молодой ученый #10 (509). Март 2024. с. 1–12.
- Гасанов И. Р., Бегляров Э. Б. О некоторых формулах для выпуклых четырехугольников. Молодой ученый #10 (509). Март 2024. с. 13–17.
- Elkhan Baylarov. Ilyas Hasanov. A Different Geometric Approch to the Proof of Fermat’s Last Theorem.
- Бегляров Э. Б. Гасанов И. Р. К вопросу применения метода n-прямых. Молодой ученый #15 (514). Апрель 2024. с. 1–9.
- Richard Kaufman. Limits on Legs of Pythagorean Triples and Fermat’s Last Theorem. The Collage Mathematics journal. 51:1, 2020, 53–56. Doi:10.1080/07468342, 2020/1674620.
- Виктор Мешеряков. Электронные материалы. Прямые в треугольнике и Великая Теорема Ферма. https://youtu.be/hoMTCd8epMy, октябрь 2022.







